专题　功与功率 题型分析

专题一 功的正负判断及计算

例1 如右图所示是某小孩滑滑梯的情景，在小孩下滑的过程中，关于各力做的功，下列说法正确的是(　　)

A．重力做正功

B．支持力做负功

C．支持力不做功

D．摩擦力做负功

解析 在小孩下滑过程中，位移方向斜向下，重力竖直向下，所以重力与位移的夹角为锐角，重力做正功，选项A正确；支持力始终与运动方向垂直，即始终与位移垂直，所以支持力不做功，选项B错误，C正确；摩擦力始终与运动方向相反，即摩擦力始终与位移方向相反，所以摩擦力做负功，选项D正确．

答案 AD

归纳总结：判定一个力是否做功、做正功还是做负功，常用的方法有两种：一是看力与位移之间的夹角，此方法常用于物体做直线运动的情况；二是看力与速度之间的夹角，此方法常用于物体做曲线运动的情况．

专题二 功的计算

例2 如图所示，水平地面上的物体质量为2 kg，在方向与水平面成37°角、大小为10 N的拉力F作用下移动2 m，已知物体与水平地面间的动摩擦因数为0.2.

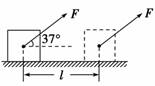
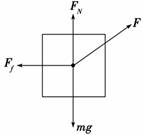
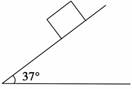
解析：物体受重力、支持力、拉力、摩擦力四个力作用，受力分析如图所示，其中重力和支持力与运动方向垂直，不做功，拉力做正功，摩擦力做负功．

解法一：拉力F对物体做的功为WF＝F·lcos 37°＝10×2×0.8 J＝16 J

摩擦力对物体做的功为

WFf＝F f lcos 180°＝－μ(mg－Fsin 37°)l＝－0.2×(2×10－10×0.6)×2 J＝－5.6 J

重力和支持力做的功为WG＝WFN＝0

合力做功为W合＝WG＋WFN＋WF＋WFf＝16 J－5.6 J＝10.4 J

解法二：物体所受到的合力为F合＝Fcos 37°－Ff＝(10×0.8－2.8) N＝5.2 N

所以W合＝F合·l＝5.2×2 J＝10.4 J.

答案：WG＝WFN＝0　WF＝16 J　WFf＝－5.6 J　W合＝  10.4 J

归纳总结：对于总功的计算，常见的求解方法有两种：(1)先对物体进行受力分析，根据功的计算式求出各个力所做的功，然后求它们的代数和．(2)先对物体进行受力分析，求出物体所受的合力，然后根据功的计算式求出合力所做的功．

专题三 摩擦力做功的特点

例3 质量为M的长木板放在光滑水平地面上，如图所示．一个质量为m的滑块以某一速度沿木板表面从A端滑到B点，在木板上前进的距离为L，而木板前进的距离为x，若滑块与木板间的动摩擦因数为μ，求：

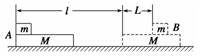
(1)摩擦力对滑块所做的功多大？

(2)摩擦力对木板所做的功多大？

解析　由题图可知，木板的位移为l时，滑块的位移为l＋L，m与M之间的滑动摩擦力Ff＝μmg.

由公式W＝Flcos α可得摩擦力对滑块所做的功为W_m＝μmgl_mcos180°＝－μmg(l＋L)，负号表示做负功．摩擦力对木板所做的功为W_M＝μmgl_M＝μmgl.

答案　(1)－μmg(l＋L)　(2)μmgl

归纳总结：

1．不能认为摩擦力总是做负功，摩擦力可以做正功，可以做负功也可以不做功，要搞清摩擦力与物体位移之间的关系，其中位移是相对地面的位移．

2．作用力与反作用力同时存在，作用力做功时，反作用力可能做功，也可能不做功，可以做正功，也可以做负功.

专题四 变力做功的计算

例4 如图所示，一质量为m＝2.0 kg的物体从半径为R＝5.0 m的圆弧的A端，在拉力作用下沿圆弧缓慢运动到B端(圆弧AB在竖直平面内)．拉力F大小不变始终为15 N，方向始终与物体在该点的切线成37°角．圆弧所对应的圆心角为60°，BO边为竖直方向，g取10 m/s².求这一过程中：

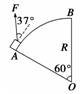
(1)拉力F做的功．

(2)重力mg做的功．

(3)圆弧面对物体的支持力FN做的功．

(4)圆弧面对物体的摩擦力Ff做的功．

解析　(1)将圆弧分成很多小段l₁，l₂，…l_n，拉力在每小段上做的功为W₁，W₂，…W_n，因拉力F大小不变，方向始终与物体在该点的切线成37°角，所以：W₁＝Fl₁cos 37°，W₂＝Fl₂cos 37°，…，W_n＝Fl_ncos 37°，所以

WF＝W₁＋W₂＋…＋W_n＝Fcos 37°(l₁＋l₂＋…＋l_n)

＝Fcos 37°·R＝20π J＝62.8 J

(2)重力mg做的功WG＝－mgR(1－cos 60°)＝－50 J

(3)物体受的支持力FN始终与物体的运动方向垂直，所以WF_N＝0.

(4)因物体在拉力F作用下缓慢移动，合外力做功为零，所以WF＋WG＋WF_f＝0.所以WF_f＝－WF－WG＝(－62.8＋50) J＝－12.8 J

答案　(1)62.8 J　(2)－50 J　(3)0　(4)－12.8 J

归纳总结：将变力的功转化为恒力的功的常用方法：

1．当力的大小不变，而方向始终与运动方向相同或相反时，这类力的功等于力和路程(不是位移)的乘积，如滑动摩擦力、空气阻力做功等等．

2．当力的方向不变，大小随位移做线性变化时，可先求出力对位移的平均值＝，再由W＝lcos α计算，如弹簧弹力做功．

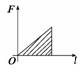
3．作出变力F随位移变化的图象，图线与横轴所夹的“面积”即为变力所做的功．如图所示.

专题五 功与动力学知识综合应用

例5 如图所示，绳的一端固定在天花板上，通过一动滑轮将质量m＝10 kg的物体由静止开始以2 m/s2的加速度提升．求作用在绳的另一端的拉力F 在3 s内所做的功．(g 取10 m/s2，滑轮和绳的质量及摩擦均不计)

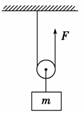
解析 物体受到两个力的作用：拉力F′和重力mg，

由牛顿第二定律得F′－mg＝ma，所以F′＝m(g＋a)＝10×(10＋2) N＝120 N

则力F＝F′＝60 N

物体由静止开始运动，3 s内的位移为l＝at2＝×2×32 m＝9 m，

在物体发生9 m的位移的过程中，拉力F的作用点的位移为2l＝18 m，

所以力F做的功为W＝F·2l＝60×18 J＝1 080 J

答案 1 080 J

归纳总结：利用公式W＝Flcos α计算功时，需要确定物体的受力F和物体对地的位移l；当物体处于平衡状态时，可利用平衡条件求力F；当物体做变速运动时，常利用牛顿第二定律求力F.而物体的位移l易和运动学的知识相联系，所以功的计算问题有时也是一个学科内综合问题．

专题六 瞬时功率和平均功率的计算

例6 如图所示，质量为m＝2 kg的木块在倾角θ＝37°的斜面上由静止开始下滑，木块与斜面间的动摩擦因数为0.5，已知sin 37°＝0.6，cos 37°＝0.8，g取10 m/s2，求：

(1)前2 s内重力做的功；

(2)前2 s内重力的平均功率；

(3)2 s末重力的瞬时功率．

解析 (1)木块所受的合外力为：F_合＝mgsin θ－μmgcos θ＝mg(sin θ－μcos θ)＝2×10× (0.6－0.5×0.8) N＝4 N．木块的加速度为：a＝＝ m/s²＝2 m/s².前2 s内木块的位移：   l＝at²＝×2×2² m＝4 m．所以，重力在前2 s内做的功为：W＝mgsin θ·l＝2×10×0.6×4 J＝48 J.

(2)重力在前2 s内的平均功率为：＝＝ W＝24 （W）.

(3)木块在2 s末的速度：v＝at＝2×2 m/s＝4 m/s.重力在2 s末的瞬时功率：

P＝mgsin θv＝2×10×0.6×4 W＝48 （W）.

答案 (1)48 J　(2)24 W　(3)48 W

归纳总结：计算功率时，首先明确要求的是平均功率还是瞬时功率，如果是平均功率，可用公式P＝或P＝Fcos α来计算；如果是瞬时功率，通常用公式P＝Fvcos α来计算．

专题七 功率和速度的关系

例7 一辆质量为2.0×103 kg的汽车以额定功率P0＝6.0×104 W在水平公路上行驶，汽车受到的阻力为一定值，在某时刻汽车的速度为v1＝20 m/s，加速度为a1＝0.50 m/s2，求(g取10 m/s2)：

    (1)汽车所能达到的最大速度vm是多大？

    (2)若汽车从静止开始做匀加速直线运动(不是额定功率行驶)，加速度大小为a2＝1.0 m/s2，则这一过程能维持多长时间？

解析　(1)汽车以额定功率P₀行驶，速度为v₁时，有

F₁－F_阻＝ma₁①

P₀＝F₁v₁②

联立①②解得F_阻＝－ma₁③

当牵引力减小到与阻力平衡时，速度达到最大值，有

v_m＝④

将数据代入③，④中，解得F_阻＝2.0×10³ N，v_m＝30 m/s.

(2)汽车由静止启动后，随着速度的增大，牵引力的功率逐渐变大，当功率达到额定功率时，机车达到匀加速直线运动所能达到的最大速度v2，设此过程中机车的牵引力为F2，由牛顿第二定律得

F2－F阻＝ma2⑤

又P0＝F2v2⑥

v2＝a2t⑦

联立解得v2＝15 m/s，t＝15 s.

答案　(1)30 m/s　(2)15 s

归纳总结：(1)机车的最大速度v_m的求法：机车达到匀速前进时速度最大，此时牵引力F等于阻力F_阻，故v_m＝＝.

(2)匀加速启动最长时间的求法：牵引力F＝ma＋F_阻，匀加速的最后速度v_m′＝，时间t＝.

(3)瞬时加速度的求法：据F＝求出牵引力，则加速度a＝/m

专题八 机车的启动问题

例8 一汽车额定功率为100 kW，质量为1.0×104 kg，设阻力恒为车重的0.1倍，取g＝10 m/s2.

(1)若汽车保持恒定功率运动，求运动的最大速度；

(2)若汽车以0.5 m/s2的加速度匀加速运动，求其匀加速运动的最长时间．

解析 (1)当a＝0，即F＝f时速度最大，设为v_max，     v_max＝＝＝ m/s＝10 m/s，以后汽车保持v_max匀速运动．

(2)匀加速启动时，汽车牵引力恒定，随着v↑^F一定P↑，直到达到额定功率后，v↑^P一定 F↓，汽车改做a减小的变加速运动，直到a＝0，达到最大速度v_max后做匀速运动．匀加速运动中，由F－f＝ma得汽车牵引力F＝ma＋f＝1.5×    10⁴ N．达到额定功率时的速度v₁＝＝ m/s＝    6.7 m/s，此为匀加速运动的末速度，所以匀加速运动的最长时间t＝＝13.4 s.

答案 (1)10 m/s　(2)13.4s

归纳总结：对机车等交通工具类问题，应明确P＝F·v中，P为发动机的实际功率．由于这类问题是一个动态变化过程，各个物理量相互关联，分析时，抓住不变量，利用P＝Fv和 F合＝ma进行逐步分析．