专题　圆周运动 题型分析

专题一 对匀速圆周运动的理解

例1  质点做匀速圆周运动，则              (　　)．

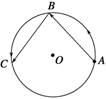
A．在任何相等的时间里，质点的位移都相等

B．在任何相等的时间里，质点通过的路程都相等

C．在任何相等的时间里，质点运动的平均速度都相同

D．在任何相等的时间里，连接质点和圆心的半径转过的角度都相等

解析　如图所示，经，质点由A到B，再经，质点由B到C，由于线速度大小不变，根据线速度的定义，Δs＝v·，所以相等时间内通过的路程相等，B对．但位移x_AB、x_BC大小相等，方向并不相同，平均速度不同，A、C错．由角速度的定义ω＝知Δt相同，Δθ＝ωΔt相同，D对．

答案　BD

归纳总结：(1)矢量的比较，首先要想到方向问题．

(2)“相等时间内…”的问题，为便于比较可以取一些特殊值，但是有时取特殊值也会犯错，如本题中若取t＝T，则相等时间内位移相等，均为0，这样看来A选项正确，所以举例时要具有普遍性．

(3)匀速圆周运动中的“匀速”，这里的“匀速”是“匀速率”的意思，匀速圆周运动是变速运动．

专题二 描述圆周运动的物理量

例2  如图所示，圆环以直径AB为轴匀速转动．已知其半径为0.5 m，周期为4 s，求环上P点和Q点的角速度和线速度．

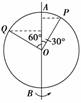
解析  P点和Q点的角速度相同，ω＝      ≈1.57 rad/s.P点和Q点绕AB轴做圆周运动，其轨迹的圆心不同，P点和Q点的圆半径分别为rp＝R·sin 30°＝R，rQ＝R·sin 60°＝R.故其线速度分别为vP＝ωrP≈0.39 m/s，vQ＝ωrQ＝0.68 m/s.

答案  ωP＝ωQ＝1.51 rad/s　vP＝0.39 m/s  vQ＝0.68 m/s.

归纳总结：明确圆周运动中各物理量间的关系，是分析圆周运动问题的基础．

专题三 传动装置中各物理量间的关系

例3  如图所示的传动装置中，B、C两轮固定在一起绕同一轴转动，A、B两轮用皮带传动，三轮半径的关系是rA＝rC ＝ 2rB.若皮带不打滑，求A、B、C三轮边缘的a、b、c三点的角速度之比和线速度之比．

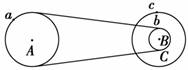
解析  A、B两轮通过皮带传动，皮带不打滑，则A、B两轮边缘上各点的线速度大小相等，即v_a＝v_b或v_av_b＝11①

由v＝ωr得ω_aω_b＝r_Br_A＝12②

B、C两轮固定在一起绕同一轴转动，则B、C两轮上各点的角速度相同，即

ω_b＝ω_c或ω_b ω_c＝11③

由v＝ωr得v_bv_c＝r_Br_C＝12④

由②③两式得ω_aω_bω_c＝122

由①④两式得v_av_bv_c＝112.

答案：ω_aω_bω_c＝122　v_av_bv_c＝112

归纳总结：解决这类问题时要注意抓住传动装置的特点：同轴转动时两轮的角速度相等，皮带传动(不打滑)时两轮边缘的线速度大小相等，求解时注意运用v＝ωr找联系．

专题四 圆周运动与其他运动相结合

例4  如右图所示，直径为d的纸制圆筒以角速度ω绕垂直纸面的轴O匀速转动(图示为截面)．从枪口发射的子弹沿直径穿过圆筒．若子弹在圆筒旋转不到半周时，在圆周上留下a、b两个弹孔．已知aO与bO夹角为θ，求子弹的速度．

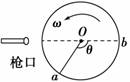
解析  设子弹速度为v，则子弹穿过圆筒的时间t＝.此时间内圆筒转过的角度α＝π－θ.据α＝ωt，得π－θ＝ω.则子弹的速度v＝.

答案  v＝.

归纳总结：有些题目会涉及圆周运动、直线运动和平抛运动等不同的运动，不同运动规律在解决同一问题时，必然有一个物理量起桥梁作用，将两种不同运动联系起来，这一物理量常常是“时间”．通常会涉及由圆周运动引起的多解问题．