专题 生活中的圆周运动 题型分析专题一 关于车转弯的分析
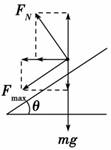
(1)若赛车的速度达到72 km/h,这辆车在运动过程中会不会发生侧移? (2)若将场地建成外高内低的圆形,且倾角为30°,并假设车轮和地面之间的最大静摩擦力不变,为保证赛车的行驶安全,赛车最大行驶速度应为多大? 解析:(1)赛车在水平场地转弯时,静摩擦力提供其转弯所需的向心力.当v=72 km/h= 20 m/s时所需的向心力 F= 可见静摩擦力可以提供圆周运动所需向心力,故车不会侧移. (2)若将场地建成外高内低的圆形,则赛车做匀速圆周运动的向心力由重力mg、支持力FN和静摩擦力的合力来提供,左下图所示为赛车做圆周运动的后视图(赛车正垂直纸面向里运动).赛车以最大速度行驶时,地面对赛车的摩擦力为最大静摩擦力Fmax.受力分析如图所示,利用正交分解法列方程,水平方向:
FN sin θ+Fmaxcos θ= 竖直方向:FN cos θ-Fmaxsin θ-mg=0, 联立以上两式得vmax= 答案:(1)不会 (2)35.6 m/s 归纳总结:汽车(自行车)在水平面上转弯时,汽车(自行车)所受地面的静摩擦力提供转弯的向心力,在倾斜路面上转弯,通常是重力与路面的支持力的合力提供向心力,转弯的圆心在水平面上,物体转弯时如做匀速圆周运动,则合力提供物体做圆周运动的向心力. 专题二 车过拱桥问题
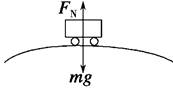
(1)若汽车到达桥顶时速度为v1=5 m/s,汽车对桥面的压力是多大? (2)汽车以多大速度经过桥顶时,恰好对桥面没有压力? (3)汽车对桥面的压力过小是不安全的,因此汽车过桥时的速度不能过大.对于同样的车速,拱桥圆弧的半径大些比较安全,还是小些比较安全? (4)如果拱桥的半径增大到与地球半径一样大,汽车要在桥面上腾空,速度至少为多大?(已知地球半径为6 400 km) 解析 如图所示,汽车到达桥顶时,受到重力mg和桥面对它的支持力FN的作用.(1)汽车对桥面的压力大小等于桥面对汽车的支持力FN.汽车过桥时做圆周运动,重力和支持力的合力提供向心力,根据牛顿第二定律有 mg-FN=m 所以FN=mg-m=7 600 N 故汽车对桥面的压力为7 600 N.
(2)汽车经过桥顶时恰好对桥面没有压力,则FN=0,即汽车做圆周运动的向心力完全由其自身重力来提供,所以有mg=m 解得v==22.4 m/s. (3)由(2)问可知,当FN=0时,汽车会发生类似平抛的运动,这是不安全的,所以对于同样的车速,拱桥圆弧的半径大些比较安全. (4)由(2)问可知,若拱桥的半径增大到与地球半径一样大,汽车要在桥面上腾空,速度至少为 v′== m/s=8 000 m/s. 答案 (1)7 600 N (2)22.4 m/s (3)半径大些比较安全
归纳总结:(1)分析汽车过桥这类问题时应把握以下两点: ①汽车在拱桥上的运动是竖直面内的圆周运动. ②汽车在桥顶时受到重力和桥面的支持力作用,这两个力的合力提供向心力. (2)解题步骤是: ①选取研究对象,确定轨道平面、圆心位置和轨道半径; ②正确分析研究对象的受力情况(切记:向心力是按作用效果命名的力,在受力分析时不能列出),明确向心力的来源;③根据牛顿运动定律列方程求解. 专题三 竖直平面内的圆周运动的临界问题
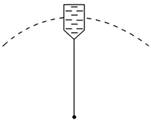
(1)若在最高点水不流出来,求桶的最小速率; (2)若在最高点水桶的速率v=3 m/s,求水对桶底的压力. 解析 分别以水桶和桶中的水为研究对象,对它们进行受力分析,找出它们做圆周运动所需向心力的来源,根据牛顿运动定律建立方程求解. (1)以水桶中的水为研究对象,在最高点恰好不流出来,说明水的重力恰好提供其做圆周运动所需的向心力,此时桶的速率最小. 此时有:mg=m, 则所求的最小速率为:v0==2.24 m/s. (2)此时桶底对水有一向下的压力,设为FN,则由牛顿第二定律有:FN+mg=m, 代入数据可得:FN=4 N. 由牛顿第三定律,水对桶底的压力:FN′=4 N. 答案 2.24 m/s (2)4 N 归纳总结:1.分析竖直面内的圆周运动,先分清是绳模型还是杆模型. 2.在这两类模型中,小球在最低点的受力情况是相同的,关键在最高点能不能受到“支撑”. 3.轻杆类小球在竖直面做圆周运动中有两个临界速度:一个是最高点v=0,是小球能够做完整圆周运动的临界速度;一个是v=,是小球在最高点不受轻杆作用力的临界速 度,它是判断轻杆对小球是拉力还是支持力的分界点.
|