专题　万有引力理论的成就  题型分析

专题一 关于天体质量的计算

例1　2020年11月28日“嫦娥五号”顺利进入环月轨道，在不久的将来我国航天员将登上月球，假设几年后我国第一位航天员登上了月球表面，如果他已知月球半径，那么他用一个弹簧测力计和一个已知质量的砝码，能否测出月球的质量？应该怎样测定？

解析：将砝码挂在弹簧测力计上，记录弹簧测力计的读数F,

由F＝mg_月，得：g月＝①

在月球表面，砝码的重力应约等于月球对其的引力：

mg_月＝G，则M＝②

将①代入②，解得M＝＝.

答案：见解析

归纳总结：在万有引力与航天这一章中，求天体质量的方法主要有两种：一种方法是根据重力加速度求天体质量，即g＝G，则M＝；另一种方法是根据天体的圆周运动，即根据天体做圆周运动的向心力由万有引力提供，列出方程：G＝mr，求得M＝.

专题二 关于天体密度的求解

例2　地球表面的平均重力加速度为g，地球半径为R，引力常量为G，可估算地球的平均密度为(　　)

A.                                                         B. 

C.                                                             D.

解析　忽略地球自转的影响，对处于地球表面的物体，有mg＝G，地球质量M＝ρV＝πR³ρ.代入上式化简可得地球的平均密度ρ＝.

答案　A

归纳总结：(1)若已知星球表面的重力加速度g和星球的半径，忽略星球自转的影响，则mg＝即GM＝gR²被称为“黄金替换”．

(2)当天体的卫星环绕天体表面运动时，其轨道半径r等于天体半径R，则天体密度ρ＝.

(3)计算天体的密度时，应注意中心天体的半径与卫星的轨道半径的不同

专题三 双星模型

例3　经长期观测，人们在宇宙中已经发现了双星系统．双星系统由两颗相距较近的恒星组成，每个恒星的线度远小于两个星体之间的距离，而且双星系统一般远离其他天体．如图所示，两颗星球组成的双星，在相互之间的万有引力作用下，绕连线上的O点做周期相同的匀速圆周运动．现测得两颗星之间的距离为L，质量之比为m1∶m2＝3∶2，下列说法中正确的是(　　)．

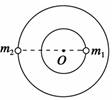
A．m1、m2做圆周运动的线速度之比为3∶2

B．m1、m2做圆周运动的角速度之比为3∶2

C．m₁做圆周运动的半径为L

D．m₂做圆周运动的半径为L

解析　设双星m₁、m₂距转动中心O的距离分别为r₁、r₂，双星绕O点转动的角速度为ω，据万有引力定律和牛顿第二定律得

G＝m₁r₁ω²＝m₂r₂ω²，又r₁＋r₂＝L，m₁∶m₂＝3∶2

所以可解得r₁＝L，r₂＝L

m₁、m₂运动的线速度分别为v₁＝r₁ω，v₂＝r₂ω故v₁∶v₂＝r₁∶r₂＝2∶3

综上所述，选项C正确．

答案　C

归纳总结：双星做匀速圆周运动的圆心相同，我们可根据它们做圆周运动的周期相同、双星之间的万有引力提供它们做圆周运动的向心力等特点进行解答．双星间的万有引力提供了它们做圆周运动的向心力．即G＝m₁ω²r₁＝m₂ω²r₂.

由此得出：

(1)m₁r₁＝m₂r₂　即r∝

(2)由于ω＝，r₁＋r₂＝L，所以两星的质量之和m₁＋m₂＝.

专题四 抛体运动与万有引力定律的结合

例4　 宇航员在地球表面以一定初速度竖直上抛一小球，经过时间t小球落回原处；若他在某星球表面以相同的初速度竖直上抛同一小球，需经过时间5t小球落回原处．(取地球表面重力加速度g＝10 m/s²，空气阻力不计)

(1)求该星球表面附近的重力加速度g′.

(2)已知该星球的半径与地球半径之比为R_星∶R_地＝1∶4，求该星球的质量与地球质量之比M_星∶M_地．

解析　 (1)在地球表面竖直上抛小球时有t＝

在某星球表面竖直上抛小球时有5t＝

所以g′＝ g＝2 m/s²

(2)由G＝mg，得M＝

所以＝＝×()²＝

答案　(1)2 m/s²　(2)1∶80

归纳总结：在天体的有关计算中，有时要利用抛体运动(平抛或竖直上抛)求天体表面的重力加速度，然后结合万有引力定律求M和ρ.