专题　机械能守恒定律  题型分析

专题一 单个物体的机械能守恒定律

例1 以10 m/s的速度将质量为m的物体从地面上竖直向上抛出，若忽略空气阻力，g取10 m/s2，则：

(1)物体上升的最大高度是多少？

(2)上升过程中在何处重力势能与动能相等？

解析 (1)由于物体在运动过程中只有重力做功，所以机械能守恒．取地面为零势能面，则E₁＝mv，在最高点动能为0，故E₂＝mgh，由机械能守恒定律E₁＝E₂可得：mv＝mgh，所以h＝＝ m＝5（m）.

(2)初态物体在地面上，E₁＝mv，设重力势能与动能相等时在距离地面h₁高处，E₂＝mv＋mgh₁＝2mgh₁，由机械能守恒定律可得：mv＝mv＋mgh₁＝2mgh₁，所以h₁＝＝2.5 m.

答案 (1)5 m　(2)2.5 m

归纳总结：在利用机械能守恒定律表达式E1＝E2解题时，由于重力势能的相对性，必须先选取参考平面，方可解题．

专题二 机械能守恒的判定

例2  如图所示，细绳跨过定滑轮悬挂两物体M和m，且M>m，不计摩擦，系统由静止开始运动过程中(　　)

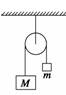
A．M、m各自的机械能分别守恒

B．M减少的机械能等于m增加的机械能

C．M减少的重力势能等于m增加的重力势能

D．M和m组成的系统机械能守恒

解析　M下落过程中，绳的拉力对M做负功，M的机械能，减少；m上升过程，绳的拉力对m做正功，m的机械能增加，A错误；对M、m组成的系统，机械能守恒，易得B、D正确；M减少的重力势能并没有全部用于m重力势能的增加，还有一部分转变成M、m的动能，所以C错误．

答案　BD

归纳总结：1．用做功来判断：分析物体或物体系的受力情况(包括内力和外力)，明确各力做功的情况，若对物体或系统只有重力或弹力做功，没有其他力做功或其他力做功的代数和为零，则机械能守恒．

2．用能量转化来判定：若物体系中只有动能和势能的相互转化而无机械能与其他形式的能的转化(如系统无滑动摩擦力和介质阻力，无化学能的释放，无电磁感应过程等)，则物体系机械能守恒．

3．对一些绳子突然绷紧、物体间碰撞等问题机械能一般不守恒，除非题目中有特别说明或暗示.

专题三 多个物体的机械能守恒

例3  如图所示，可视为质点的小球A、B用不可伸长的细软轻线连接，跨过固定在地面上半径为R的光滑圆柱，A的质量为B的两倍．当B位于地面时，A恰与圆柱轴心等高．将A由静止释放，B上升的最大高度是   (　　)

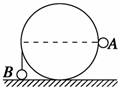
A．2R                                                           B. 

C.                                                             D.

解析　设A、B的质量分别为2m、m，当A落到地面上时，B恰好运动到与圆柱轴心等高处，以A、B整体为研究对象，则A、B组成的系统机械能守恒，故有2mgR－mgR＝(2m＋m)v²，A落到地面上以后，B以速度v竖直上抛，又上升的高度为h′＝，解得h′＝R，故B上升的总高度为R＋h′＝R，选项C正确．

答案　C

归纳总结：由多个物体组成的系统机械能守恒问题常有多种解法，既可以用系统机械能守恒进行求解，也可以针对各物体用动能定理进行求解，解题时可任选其中的一种．本类型题易错点是误认为mA、mB单个物体机械能守恒．

专题四 机械能守恒定律的简单应用

例4  以20 m/s的速度将一物体竖直上抛，若忽略空气阻力，g取10 m/s²，试求：

(1)物体上升的最大高度．

(2)以水平地面为参考平面，物体在上升过程中重力势能和动能相等的位置．

解析　(1)设物体上升的最大高度为H，在物体上升的整个过程中应用机械能守恒定律，有mgH＝mv解得H＝＝ m＝20 m

(2)设物体重力势能和动能相等的位置距地面的高度为h，此时物体的速度为v，则有

mgh＝mv²

以物体被抛出到运动至该位置的过程中应用机械能守恒定律，有mgh＋mv²＝mv

由以上两式解得h＝＝ m＝10 m

答案　(1)20 m　(2)10 m

专题五 关于物体系统中的机械能守恒问题

例5  如右图所示是一个横截面为半圆、半径为R的光滑柱面，一根不可伸长的细绳两端分别系着物体A、B，且mA＝2mB，由图示位置从静止开始释放物体A，当物体B达到圆柱顶点时，求绳的张力对物体B所做的功．

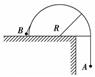
解析 系统重力势能的减少量为ΔE_p＝m_Ag－m_Bg_R，系统动能的增加量为ΔE_k＝(m_A＋m_B)v²

由ΔE_p＝ΔE_k得v²＝(π－1)gR

绳的张力对物体B做的功W＝m_Bv²＋m_BgR＝m_BgR.

答案 m_BgR

归纳总结：对于相互作用的整体，在进行能量转化时，单独一个物体机械能一般不守恒，但系统机械能守恒，可利用机械能守恒定律对系统列方程求解相关量．

专题六 动能定理和机械能守恒定律的综合应用

例6  如图所示，在竖直平面内有一固定光滑轨道，其中AB是长为R的水平直轨道，BCD是圆心为O、半径为R的圆弧轨道，两轨道相切于B点．在外力作用下，一小球从A点由静止开始做匀加速直线运动，到达B点时撤除外力．已知小球刚好能沿圆弧轨道经过最高点C，重力加速度大小为g.求：

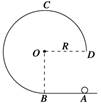
(1)小球在AB段运动的加速度的大小；

(2)小球从D点运动到A点所用的时间．

解析　(1)小球在最高点C所受轨道的正压力为零，设小球在C点的速度大小为v_C，根据牛顿第二定律有mg＝m

小球从B点运动到C点的过程中，机械能守恒．设小球在B点的速度大小为v_B，则有

mv＝mv＋2mgR

小球在AB段由静止开始做匀加速运动，设加速度大小为a，由运动学公式得v＝2aR

联立以上各式解得a＝g

(2)设小球在D点的速度大小为v_D，下落到A点时的速度大小为v，根据机械能守恒定律，小球从B点运动到D点的过程，有mv＝mv＋mgR

小球从B点运动到A的过程，有mv＝mv²

设小球从D点运动到A点所用的时间为t，根据运动学公式有gt＝v－v_D

解得t＝(－).

答案　(1)g　(2)(－)

归纳总结：在读、审题时要把握好以下几点：

(1)要分清是全过程还是某一个过程机械能守恒．

(2)抓好竖直面内圆周运动的临界条件．

(3)列好辅助方程(牛顿第二定律方程)．