专题　向心加速度  题型分析

专题一 速度的变化量

例1  物体以初速度v0做平抛运动，经一段时间(未落地)速度大小变为v，如图所示．则此过程中物体速度变化量的大小和方向分别为(　　)

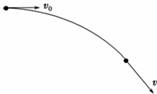
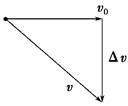
A．v－v₀，水平向右     B．v₀－v，水平向左

C.，竖直向下    D.，方向无法确定

解析　平抛物体运动一段时间后末速度方向与初速度方向不在同一直线上，作出如图所示，因平抛运动加速度为g，故Δv方向竖直向下，与v₀方向垂直，且Δv＝，方向竖直向下．

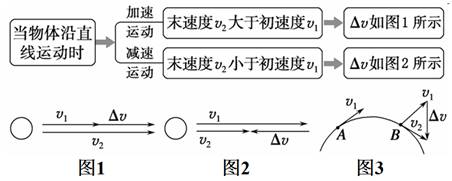
答案　C

归纳总结：速度的变化量的计算

(1)同一直线上的速度的变化量

(2)不在同一直线上的速度的变化量

当v1和v2不在同一直线上时，物体做曲线运动，如图3所示．作图时将初速度v1平移到B点，从v1的末端作Δv至v2的末端，则Δv即速度的变化量．

专题二 对向心加速度的认识

例2  如图所示，为A、B两质点做匀速圆周运动的向心加速度随半径变化的图象，其中A为双曲线的一个分支，由图可知(　　)

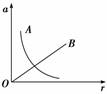
A．A物体运动的线速度大小不变

B．A物体运动的角速度大小不变

C．B物体运动的角速度大小不变

D．B物体运动的线速度大小不变

解析  搞清向心加速度公式an＝和an＝ω2r的适用条件． an＝说明线速度不变时，加速度与半径成反比，故选项A正确；an＝ω2r说明角速度不变时，加速度与半径成正比，故选项C正确．

答案  AC

归纳总结：在利用图象解决物理问题时，要注意充分挖掘图象中所携带的信息，如：一个量随另一个量如何变化；变化的确切数量关系；斜率多大，其物理意义是什么；截距、面积各有什么意义等．同时还要注意把物理图象和具体的物理情景结合起来考虑应该选取哪一个规律或公式解决问题．

专题三 向心加速度的计算

例3  滑板运动是一种时尚而又刺激的运动，目前，受到越来越多青少年的喜爱．如图所示，某滑板运动员恰好从B点进入半径为2.0 m的圆弧，该圆弧轨道在C点与水平轨道

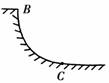
解析  运动员经圆弧滑到C点时做圆周运动．因为不计各种阻力．故经过C点之前的瞬间运动员只在竖直方向上受力，故此时他只有向心加速度．由an＝得运动员到达C点前的瞬时加速度a1＝m/s2＝50 m/s2，方向竖直向上．运动员滑过C点后，进入水平轨道做匀速直线运动，故加速度a2＝0.

答案  50 m/s2，方向竖直向上；0

归纳总结：求解圆周运动的向心加速度时，应注意根据所给已知条件灵活选用向心加速度公式a_n＝＝rω²＝²r＝vω的不同形式解题．

专题四 向心加速度的表达式的应用

例4  如图所示，一个球绕中心轴线OO′以角速度ω做匀速圆周运动，则(　　)

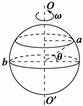
A．a、b两点的线速度相同

B．a、b两点的角速度相同

C．若θ＝30°，则a、b两点的线速度之比v_a∶v_b＝∶2

D．若θ＝30°，则a、b两点的向心加速度之比a_a∶a_b＝∶2

解析　由于a、b两点在同一球体上，因此a、b两点的角速度ω相同，B正确；由v＝ωr知v_a<v_b，A错误；又r_a＝r_bcos θ，则当θ＝30°时，r_a＝r_b，则v_a∶v_b＝r_a∶r_b＝∶2，C正确；由a_n＝ω²r知a_a∶a_b＝r_a∶r_b＝∶2，D正确．

答案　BCD

归纳总结：向心加速度的每个公式都涉及三个物理量的变化关系，所以必须在某一物理量不变时，才可以判断另外两个物理量之间的关系．在v一定的情况下，可认为物体的向心加速度an与R成反比；而在ω一定的情况下，可认为物体的向心加速度an与R成正比．

专题五 传动装置的向心加速度的计算

例5  如图所示，O、O1，为两个皮带轮，O轮的半径为r，O1轮的半径为R，且R>r，M点为O轮边缘上的一点，N点是O1轮上的任意一点，当皮带转动时(设转动过程中不打滑)，则(　　)

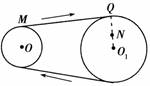
A．M点的向心加速度一定大于N点的向心加速度

B．M点的向心加速度一定等于N点的向心加速度

C．M点的向心加速度可能小于N点的向心加速度

D．M点的向心加速度可能等于N点的向心加速度

解析 因为两轮的转动是通过皮带传动的，而且皮带在转动过程中不打滑，故两轮边缘各点的线速度大小一定相等．在大轮边缘上任取一点Q，因为R>r，所以由an＝可知，aQ<aM，再比较Q、N两点的向心加速度的大小，因为Q、N是在同一轮上的两点，所以角速度ω相等．又因为RQ>RN，则由    an＝ω2r可知，aQ>aN，综上可见，aM>aN，因此选项A正确．

答案 A

归纳总结：分析本题的关键有两点：其一是同一轮上的各点角速度相同；其二是皮带不打滑时，与皮带接触的各点线速度相同．抓住了这两点，再根据描述圆周运动的各物理量之间的关系就不难得出正确结论．