专题　重力势能  题型分析

专题一 重力势能的计算

例1 金茂大厦是上海的标志性建筑之一，它主体建筑地上88层，地下3层，高420.5 m，是目前国内第一、世界第三的高楼，如图所示．距地面341 m的第88层为国内迄今最高的观光层，环顾四周，极目眺望，上海新貌尽收眼底，质量为60 kg的游客，在下列情况中，他的重力势能各是多少？(g取10 m/s2)

(1)以地面为参考平面；

(2)以第88层为参考平面；

(3)以420.5 m的楼顶为参考平面，若他乘电梯从地面上升到88层，需克服重力做多少功？

解析 (1)以地面为参考平面，游客在88层的相对高度为341 m，则Ep1＝mgh＝60×10×341 J≈2.0×105 J.

(2)若以88层处为参考平面，游客在88层的相对高度为0，故Ep2＝0.

(3)克服重力做的功与参考平面的选择无关，只与相对高度差有关，则W1＝mgh＝2.0×105 J.

答案 (1)2.0×105 J　(2)0　(3)2.0×105 J

归纳总结：(1)物体的重力势能的大小是相对的，其数值与参考平面的选择有关．

(2)重力势能的变化是绝对的，与参考平面的选择无关，其变化量仅由重力对物体做功的多少来决定．

专题二 重力做功与重力势能变化

例2 质量相等的均质柔软细绳A、B平放于水平地面，绳A较长．分别捏住两绳中点缓慢提起，直到全部离开地面，两绳中点被提升的高度分别为hA、hB，上述过程中克服重力做的功分别为WA、WB.若(　　)．

A．hA＝hB，则一定有WA＝WB

B．hA>hB，则可能有WA<WB

C．hA<hB，则可能有WA＝WB

D．hA>hB，则一定有WA>WB

解析　设绳长为l，捏住细绳中点缓慢提起，则细绳的重心在距离最高点位置处，因此细绳A的重心上升的高度为h′_A＝h_A－，细绳B的重心上升的高度为h′_B＝h_B－.由于细绳A较长，所以>，若h_A＝h_B，则A的重心较低，故一定有W_A<W_B，选项A错误；若h_A>h_B，则无法确定两细绳的重心谁高谁低，因此可能有W_A<W_B，也可能有W_A＝W_B，还可能有W_A>W_B，选项B正确，D错误；若h_A<h_B，则一定是A的重心较低，因此一定有W_A<W_B，选项C错误．

答案　B

归纳总结：功是能量转化的量度，重力势能的变化是由重力做功引起的，并且重力做多少功，重力势能就改变多少．

专题三 重心变化类物体重力势能变化

例3 如图所示，一条铁链长为2 m，质量为10 kg，放在水平地面上，拿住一端提起铁链直到铁链全部离开地面的瞬间，物体克服重力做功为多少？物体的重力势能变化了多少？(g取10 m/s2)

解析 铁链从初状态到末状态，它的重心位置提高了    h＝，因而物体克服重力所做的功为W＝mgl＝×10×10× 2 J＝100 J，铁链的重力势能增加了100 J.

铁链重力势能的变化还可由初、末状态的重力势能来分析．设铁链初态所在水平位置为零势能参考平面，则E_p1＝0，E_p2＝，铁链重力势能的变化量ΔE_p＝E_p2－E_p1＝mgl＝   ×10×10×2 J＝100 J，即铁链重力势能增加了100 J.

答案 100 J　增加了100 J

归纳总结：重力势能具有相对性，其值与参考平面的选择有关；而重力势能的变化具有绝对性，与参考平面的选择无关．在解题过程中需要注意：

(1)灵活选择零势能面可简化求解重力势能变化的过程．

(2)重力势能变化的求解仍需借助科学的思维方法，如公式法、转化法、整体法、隔离法等．

专题四 关于弹性势能的理解

例4 关于弹性势能，下列说法正确的是 (　　)

A．发生弹性形变的物体都具有弹性势能

B．只有弹簧在发生弹性形变时才具有弹性势能

C．弹性势能可以与其他形式的能相互转化

D．弹性势能在国际单位制中的单位是焦耳

解析　发生弹性形变的物体的各部分之间由于有弹力的相互作用都具有弹性势能，A正确，B错误；弹性势能跟重力势能一样，可以与其他形式的能相互转化，C正确；所有能的单位跟功的单位相同，在国际单位制中的单位是焦耳，D正确．

答案　ACD

专题五 弹力做功与弹性势能的变化

例5 如图所示，一轻弹簧一端固定于O点，另一端系一重物，将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速地释放，让它自由摆下，不计空气阻力，在重物由A点摆向最低点B的过程中   (　　)

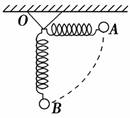
A．重力做正功，弹力不做功

B．重力做正功，弹力做负功，弹性势能增加

C．若用与弹簧原长相等的细绳代替弹簧后，重力做正功，弹力不做功

D．若用与弹簧原长相等的细绳代替弹簧后，重力做功不变，弹力不做功

解析　用细绳拴住小球向下摆动时重力做正功，弹力不做功，C对．用弹簧拴住小球下摆时，弹簧要伸长，小球轨迹不是圆弧，弹力做负功，弹性势能增加，重力做正功，且做功多，所以A、D错，B对．

答案　BC

归纳总结1．解决此类问题必须理解弹力做功与弹性势能变化之间的关系，即：弹性势能的改变仅与弹力做功有关，弹力做多少正功，弹性势能就减少多少；弹力做多少负功，弹性势能就增加多少．

2．弹簧的弹力为变力，做题时往往忽视这个问题，功的表达式W＝Flcos α中F要求为恒力，用此公式直接来求弹力做功是错误的.

专题六 弹力做功的求解

例6 如图所示，在水平地面上竖直放置一轻质弹簧，弹簧上端与一个质量为2.0 kg的木块相连．若在木块上再作用一个竖直向下的变力F，使木块缓慢向下移动0.1 m，力F做功2.5 J时，木块再次处于平衡状态，此时力F的大小为50 N．(取g＝10 m/s2)求：

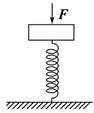
       (1)弹簧的劲度系数．

       (2)在木块下移0.1 m的

       过程中弹性势能的增加量．

解析　(1)设木块开始静止时，弹簧的压缩量为l1，后来静止时，弹簧的压缩量为l2，由胡克定律及平衡条件得，

未施加力F时，弹力F1＝mg＝kl1＝20 N，

施加力F后，弹力F2＝F＋mg＝kl2＝70 N，

且l2－l1＝0.1 m，

联立以上各式得k＝500 N/m.

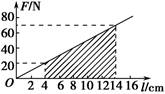
(2)由以上方程得l₁＝0.04 m，l₂＝0.14 m，根据以上数据作出F－l图象如图所示．在木块下移0.1 m的过程中，弹力做负功，且W＝－S_阴影＝－×(20＋70)×0.1 J＝－4.5 J.

所以弹性势能的增加量ΔE_p＝－W＝4.5 J.

答案　(1)500 N/m　(2)4.5 J

归纳总结：1．弹簧弹力是变力，拉伸弹簧时拉力做的功不能用恒力做功的公式计算．

2．F—l图象与横轴所围的“面积”等于拉伸弹簧时拉力所做的功，这是计算变力做功

常用的方法.