专题　动能和动能定理  题型分析

专题一 对于动能定理的理解

例1 一质量为0.1 kg的小球，以5 m/s的速度在光滑水平面上匀速运动，与竖直墙壁碰撞后以原速率反弹，若以弹回的速度方向为正方向，则小球碰撞过程中的速度变化和动能变化分别是(　　)

A．Δv＝10 m/s         B．Δv＝0

C．ΔEk＝1 J             D．ΔEk＝0

解析　速度是矢量，故Δv＝v2－v1＝5 m/s－(－5 m/s)＝10 m/s.而动能是标量，初、末两态的速度大小相等，故动能相等，因此ΔEk＝0，选A、D.

答案　AD

归纳总结

1．动能定理反映了其他形式的能通过做功和动能之间的转化关系，只不过在这里其他形式的能并不出现，而以外力做功的形式表现而已．

2．W的求法：动能定理中的W表示的是合力的功，可以应用W＝F_合·lcos α(仅适用于恒定的合外力)计算，还可以先求各个力的功再求其代数和W＝W₁＋W₂＋…＋W_n.

3．W的含义：是指包含重力在内的任意外力的总功或合外力的功，要注意以下对应关系：

 

4.在应用动能定理解题时一般要注意什么力做功，对应什么能量转化，如合力做功对应动能的变化，不必考虑其他形式能量的变化情况，同理重力或弹力做功对应重力或弹性势能的变化，不必考虑其他能量的变化情况.

专题二 动能定理的理解及应用

例2 如图所示，ABCD为一竖直平面内的轨道，其中BC水平，A点比BC高出10 m，BC长1 m，AB和CD轨道光滑．一质量为1 kg的物体，从A点以4 m/s的速度开始运动，经过BC后滑到高出C点10.3 m的D点速度为零．(g取10 m/s2)求：

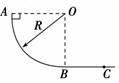
(1)物体与BC轨道间的动摩擦因数．

(2)物体第5次经过B点时的速度．

(3)物体最后停止的位置(距B点多少米)．

解析　(1)由动能定理得－mg(h－H)－μmgs_BC＝0－mv，

解得μ＝0.5.

(2)物体第5次经过B点时，物体在BC上滑动了4次，由动能定理得

mgH－μmg·4s_BC＝mv－mv，解得v₂＝4 m/s≈13.3 m/s.

(3)分析整个过程，由动能定理得mgH－μmgs＝0－mv，

解得s＝21.6 m.

所以物体在轨道上来回运动了10次后，还有1.6 m，故距B点的距离为2 m－1.6 m＝0.4 m.

答案　(1)0.5　(2)13.3 m/s　(3)距B点0.4 m

归纳总结：应用动能定理解题的步骤

(1)选取研究对象，明确并分析运动过程

(2)分析研究对象的受力情况和各力做功情况，确定求总功的思路，求出总功．

(3)明确过程始、末状态的动能Ek1和Ek2.

(4)列方程W＝Ek2－Ek1，必要时注意分析题目潜在的条件，补充方程进行求解．

专题三 应用动能定理求解变力做功

例3 如图所示，AB为圆弧轨道，BC为水平直轨道，圆弧的半径为R，BC的长度也是R.一质量为m的物体，与两个轨道的动摩擦因数都为μ，当它由轨道顶端A从静止下滑时，恰好运动到C处停止，那么物体在AB段克服摩擦力做的功为(　　)

A.μmgR                          B. mgR

C．mgR                             D．(1－μ)mgR

解析 物体从A到B所受弹力要发生变化，摩擦力大小也要随之发生变化，所以求克服摩擦力做的功，不能直接用功的公式求得．而在BC段克服摩擦力所做的功，可直接求得．对从A到C全过程应用动能定理即可求出在AB段克服摩擦力所做的功．

设物体在AB段克服摩擦力所做的功为WAB，物体从A到C的全过程，根据动能定理有mgR－WAB－μmgR＝0

所以有WAB＝mgR－μmgR＝(1－μ)mgR.

答案 D

归纳总结：利用动能定理求解变力做功时，首先要注意哪些力是变力，哪些力是恒力，找出恒力做的功和变力做的功，然后再利用动能定理解题．

专题四 动能定理和图象的综合应用

例4 摩天大楼中一部直通高层的客运电梯，行程超过百米，电梯的简化模型如图7－7－6甲所示．考虑安全、舒适、省时等因素，电梯的加速度a是随时间t变化的．已知电梯在t＝0时由静止开始上升，a－t图象如图乙所示．电梯总质量m＝2.0×103 kg.忽略一切阻力，重力加速度g取10 m/s2.

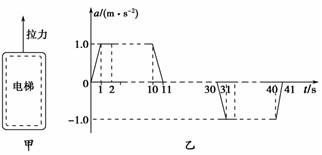
(1)求电梯在上升过程中受到的最大拉力F1和最小拉力F2；

(2)类比是一种常用的研究方法．对于直线运动，教科书中讲解了由v－t图象求位移的方法．请你借鉴此方法，对比加速度和速度的定义，根据图乙所示a－t图象，求电梯在第1 s内的速度改变量Δv1和第2 s末的速率v2；

(3)求电梯以最大速率上升时，拉力做功的功率P；再求在0～11 s时间内，拉力和重力对电梯所做的总功W.

解析　(1)根据牛顿第二定律，有F－mg＝ma

由a－t图象可知，F1和F2对应的加速度分别是

a1＝1.0 m/s2，a2＝－1.0 m/s2

所以有F1＝m(g＋a1)＝2.0×103×(10＋1.0)N＝2.2×104 N

F2＝m(g＋a2)＝2.0×103×(10－1.0)N＝1.8×104 N

(2)通过类比可得，第1 s内的速度改变量Δv1等于第1 s内a－t图线下的面积，故有

Δv1＝0.50 m/s同理可得Δv2＝v2－v0＝1.5 m/s

又v0＝0，所以第2 s末的速率v2＝1.5 m/s

(3)由a－t图象可知，11～30 s内电梯的速率最大，其值等于0～11 s内a－t图线下的面积，则有vm＝10 m/s

此时电梯做匀速运动，拉力F等于重力mg，故此时拉力做功的功率为

P＝Fvm＝mgvm＝2.0×103×10×10 W＝2.0×105 W

在0～11 s时间内，根据动能定理可得拉力和重力对电梯所做的总功为

W＝E_k2－E_k1＝mv－0＝×2.0×10³×10² J＝1.0×10⁵ J

答案　(1)F1＝2.2×104 N　F2＝1.8×104 N

(2)Δv1＝0.50 m/s　v2＝1.5 m/s

(3)P＝2.0×105 W　W＝1.0×105 J

专题五 应用动能定理求解多过程问题

例5 如图所示，一质量为2 kg的铅球从离地面2 m高处自由下落，陷入沙坑2 cm深处，求沙子对铅球的平均阻力．(g取10 m/s2)

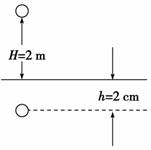
解析 铅球的运动分成自由下落和陷入沙坑做变速运动两个过程，根据动能定理，分段列式或全程列式，都可求出平均阻力．

解法一：分段列式．设铅球自由下落到沙面时的速度为v，则mgH＝mv2－0

设铅球在沙中受到的阻力为F，则mgh－Fh＝0－mv2

代入数据可得F＝2 020 N.

解法二：根据全程列式．在铅球运动的全过程中，重力做功mg(H＋h)，进入沙中阻力做功－Fh，全程动能变化量为零，则由W＝Ek2－Ek1得mg(H＋h)－Fh＝0

解得F＝2 020 N.

答案 2 020 N

归纳总结：如果物体在几个力(其中一个力未知)的作用下，运动的位移和其动能变化已知时，可用动能定理求解此未知力，当所研究的问题中涉及不止一个物体或不止一个运动过程时，可以根据解决问题的方便选取不同的物体或过程应用运能定理列方程，可以对整个过程，也可以选取其中几个过程分别列方程．

专题六 动能定理与曲线运动的综合应用

例6 某兴趣小组设计了如图所示的玩具轨道，其中“2008”四个等高数字用内壁光滑的薄壁细圆管弯成，固定在竖直平面内(所有数字均由圆或半圆组成，圆半径比细管的内径大得多)，底端与水平地面相切．弹射装置将一个小物体(可视为质点)以v0＝5 m/s的水平初速度由a点弹出，从b点进入轨道，依次经过“8002”后从P点水平抛出．小物体与地面ab段间的动摩擦因数μ＝0.3，不计其他机械能损失．已知ab段长L＝1.5 m，数字“0”的半径R＝0.2 m，小物体质量m＝0.01 kg，g＝10 m/s2.求：

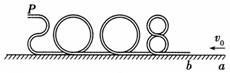
(1)小物体从P点抛出后的水平射程．

(2)小物体经过数字“0”的最高点时管道对小物体作用力的大小和方向．

解析 (1)设小物体运动到P点时的速度大小为v，对小物体由a运动到P的全过程应用动能定理得

－μmgL－mg·2R＝mv²－mv²₀①

小物体由P点抛出后做平抛运动，则2R＝gt²②

s＝vt③

联立①②③式，代入数据解得s＝0.8 m.

(2)小物体运动至数字“0”的最高点时速度大小为v，设管道对小物体的作用力为F，取竖直向下为正方向，有F＋mg＝m　④

联立①④式，代入数据解得F＝0.3 N，方向竖直向下．

答案 (1)0.8 m　(2)0.3 N，方向竖直向下

归纳总结：动能定理在处理变力、曲线运动的问题时，具有独特的优势，所以有很多考题将动能定理与圆周运动、平抛运动的知识综合起来考查．解决此类问题的关键是利用“程序法”将“大过程”分成几个“小阶段”或“状态”，然后再分别应用相关知识列出方程联立求解．