 专题 运动的合成与分解 题型分析
专题 运动的合成与分解 题型分析
专题一 运动的合成和分解
 例1
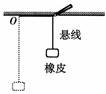
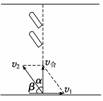
例1 如图所示,一块橡皮用细线悬挂于O点,用铅笔靠着线的左侧水平向右匀速移动,运动中始终保持悬线竖直,则橡皮运动的速度( )
如图所示,一块橡皮用细线悬挂于O点,用铅笔靠着线的左侧水平向右匀速移动,运动中始终保持悬线竖直,则橡皮运动的速度( )
A.大小和方向均不变
B.大小不变,方向改变
C.大小改变,方向不变
D.大小和方向均改变
解析 橡皮参与了两个分运动,一个是沿水平方向与铅笔速度相同的匀速直线运动,另一个是沿竖直方向与铅笔移动速度大小相等的匀速直线运动,这两个直线运动的合运动是斜向上的匀速直线运动,故选项A正确.
答案 A
归纳总结:运动的合成与分解是研究曲线运动规律最基本的方法,它的指导思想是化曲为直、化变化为不变、化复杂为简单的等效处理观点
专题二 运动的合成与分解的特性
 例2
例2 某年冬季,欧洲东部一些国家受到严重的暴风雪袭击,当局不得不出动军用直升机为被困灾民空投物资.直升机空投物资时,可以停留在空中不动,设投出的物资离开飞机后由于降落伞的作用在空中能匀速下落,无风时落地速度为5 m/s.若飞机停留在离地面100 m高处空投物资,由于风的作用,使降落伞和物资获得1 m/s的水平向北的速度,求:
某年冬季,欧洲东部一些国家受到严重的暴风雪袭击,当局不得不出动军用直升机为被困灾民空投物资.直升机空投物资时,可以停留在空中不动,设投出的物资离开飞机后由于降落伞的作用在空中能匀速下落,无风时落地速度为5 m/s.若飞机停留在离地面100 m高处空投物资,由于风的作用,使降落伞和物资获得1 m/s的水平向北的速度,求:
(1)物资在空中运动的时间;
(2)物资落地时速度的大小;
(3)物资在下落过程中水平方向移动的距离.
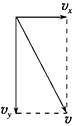
解析 如图所示,物资的实际运动可以看做是竖直方向的匀速直线运动和水平方向的匀速直线运动两个分运动的合运动.
(1)分运动与合运动具有等时性,故物资实际运动的时间与竖直方向分运动的时间相等.
所以t== s=20 s
(2)物资落地时vy=5 m/s,vx=1 m/s,由平行四边形定则得
v== m/s= m/s
(3)物资水平方向的位移大小为x=vxt=1×20 m=20 m.
答案 (1)20 s (2) m/s (3)20 m
归纳总结:合运动与分运动关系的四个特性
(1)等效性:各分运动的共同效果与合运动的效果相同.
(2)等时性:各分运动与合运动同时发生和结束,时间相同.
(3)独立性:各分运动之间互不相干,彼此独立,互不影响.
(4)同体性:各分运动与合运动是同一物体的运动.
专题三 小船渡河问题
 例3
例3 一小船渡河,河宽d=180 m,水流速度v1=2.5 m/s.船在静水中的速度为v2=5 m/s,求
一小船渡河,河宽d=180 m,水流速度v1=2.5 m/s.船在静水中的速度为v2=5 m/s,求 :
:
(1)欲使船在最短的时间内渡河,船头应朝什么方向?用多长时间?位移是多少?
(2)欲使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多少?
解析 将船实际的速度(合速度)分解为垂直河岸方向和平行河岸方向的两个分速度,垂直分速度影响渡河的时间,而平行分速度只影响平行河岸方向的位移.
(1)欲使船在最短时间内渡河,船头应朝垂直河岸方向.
当船头垂直河岸时,如右图所示,
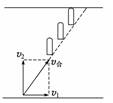
合速度为倾斜方向,垂直分速度为v2=5 m/s.
t=== s=36 s
v合== m/s
x=v合t=90 m
(2)欲使船渡河航程最短,应垂直河岸渡河.船头应朝上游与河岸成某一角度β.
垂直河岸渡河要求v水平=0,所以船头应向上游偏转一定角度,如右图所示,有v2sin
α=v1,得α=30°,所以当船头向上游偏与河岸成一定角β=60°时航程最短.
x=d=180 m t=== s=24 s
答案 (1)垂直河岸 36 s 90 m (2)偏上游与河岸成60°角 24 s 180 m
归纳总结:1.不论水流速度多大,船身垂直于河岸渡河,时间最短,tmin=,且这个时间与水流速度大小无关.
2.当v水<v船时,合运动的速度可垂直于河岸,最短航程为河宽.
3.当v水>v船时,船不能垂直到达河对岸,但仍存在最短航程,当v船与v合垂直时,航程最短,最短航程为xmin=d.
专题四 绳子末端速度的分解问题
 例4
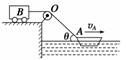
例4 如图所示,用船A拖着车B前进,若船匀速前进,速度为vA,当OA绳与水平方向夹角为θ时,求:
如图所示,用船A拖着车B前进,若船匀速前进,速度为vA,当OA绳与水平方向夹角为θ时,求:
(1)车B运动的速度vB多大?
(2)车B是否做匀速运动?
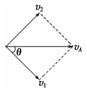
解析 (1)把vA分解为一个沿绳子方向的分速度v1和一个垂直于绳的分速度v2 ,如图所示,所以车前进的速度vB应等于vA的分速度v1,即vB=v1=vAcos θ.
,如图所示,所以车前进的速度vB应等于vA的分速度v1,即vB=v1=vAcos θ.
(2)当船匀速向前运动时,θ角逐渐减小,车速vB将逐渐增大,因此,车B不做匀速运动.
答案 (1)vAcos θ (2)B不做匀速运动
归纳总结:1.速度分解的一个基本原则就是按实际效果来进行分解.物体的实际运动方向就是合速度的方向,然后分析由这个合速度所产生的实际效果,以确定两个分速度的方向.
2.跨过定滑轮物体拉绳(或绳拉物体)运动的速度分解:物体速度v沿绳方向的分速度就是绳子拉长或缩短的速度,另一个分速度就是使绳子摆动的速度.
3.通过绳子的速度去找绳子连着的两物体间速度的关系.
(责任编辑:admin)