专题　向心力  题型分析

专题一 向心力的来源问题

例1 一个圆盘绕通过圆盘的中心O且垂直于盘面的竖直轴匀速转动，在圆盘上距O点为R处放一个质量为m的物块，物块随着圆盘一起做匀速圆周运动，如图所示．

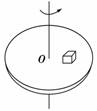
(1)物块受几个力作用，力的方向如何？

(2)向心力由什么力提供？

(3)如果物块与圆盘之间的动摩擦因数为μ，则当圆盘的角速度大于多少时，物块与圆盘之间开始滑动？

解析 (1)物块受到竖直向下的重力、竖直向上的弹力和摩擦力作用(如图所示)，摩擦力的方向始终指向圆心．

(2)向心力由摩擦力提供．

(3)设摩擦力提供向心力产生的最大角速度为ω₀，则有μmg＝mRω₀，解ω₀＝

故当ω> 时，物块将在圆盘上滑动．

答案  (1)见解析　(2)摩擦力　(3)

归纳总结：圆周运动中对向心力进行分析，往往是解题的关键，向心力的来源及作用可归纳如下：①向心力可能是物体受到的某一个力或某几个力的合力，也可能是某一个力的分力．②物体做匀速圆周运动时，合外力一定是向心力，方向指向圆心，只改变速度的方向．③物体做变速圆周运动时，合外力沿半径方向的分力充当向心力，改变速度的方向；合外力沿轨道切线方向的分力改变速度的大小．

专题二 圆周运动的一般动力学问题

例2 一个内壁光滑的圆锥筒的轴线是竖直的，圆锥固定，有质量相同的两个小球A和B贴着筒的内壁在水平面内做匀速圆周运动，如下图所示，A的运动半径较大，则(　　)

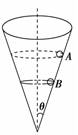
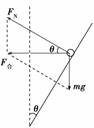
A．A球的角速度必小于B球的角速度

B．A球的线速度必小于B球的线速度

C．A球运动的周期必大于B球运动的周期

D．A球对筒壁的压力必大于B球对筒壁的压力

解析  两球均贴着筒的内壁在水平面内做匀速圆周运动，它们均受到重力和筒壁对它们的弹力作用，这两个力的合力提供向心力，如右图所示，可知筒壁对小球的弹力FN＝，而重力和弹力的合力为F合＝mgcotθ，由牛顿第二定律可得:

mgcot θ＝mω²R＝＝

所以ω＝ ①

v＝②

T＝2π ③

FN＝④

由于A球运动的半径大于B球运动的半径，由①式可知A球的角速度必小于B球的角速度；由②式可知A球的线速度必大于B球的线速度；由③式可知A球的运动周期必大于B球的运动周期；由④式可知A球对筒壁的压力一定等于B球对筒壁的压力．所以选项A、C正确．

答案  AC

归纳总结：物体做匀速圆周运动，其向心力公式可归纳为Fn＝m＝mω2r＝mr       ＝mωv.在应用的过程中，具体用哪一个，可根据题目所涉及的物理量而定．

专题三 圆周运动的临界问题

例3  如图所示，细绳一端系着质量为M＝0.6 kg的物体，静止在水平盘面上，另一端通过光滑小孔吊着质量m＝0.3 kg的物体，M的中心与小孔距离为0.2 m，并知M和水平盘面的最大静摩擦力为2 N．现使此水平盘绕中心轴转动，问角速度ω在什么范围内m处于静止状态？(g取10 m/s²)

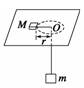
解析　设物体M和水平盘面保持相对静止，当ω具有最小值时，M有向着圆心O运动的趋势，故水平盘面对M的摩擦力方向背向圆心，且等于最大静摩擦力F_max＝2 N.

对于M：F－F_max＝Mrω

则ω₁＝ ＝ ＝ rad/s≈2.9 rad/s

当ω具有最大值时，M有离开圆心O的趋势，水平盘面对M摩擦力的方向指向圆心，F_max＝2 N.

对M有：F＋F_max＝Mrω

则ω₂＝ ＝ ＝ rad/s≈6.5 rad/s

故ω的范围是2.9 rad/s≤ω≤6.5 rad/s.

答案　2.9 rad/s≤ω≤6.5 rad/s

归纳总结：1．分析圆周的临界问题，令物体达到极限状态，暴露出临界的条件．

2．物体受静摩擦力时，要注意其大小和方向随转速的变化而发生变化，当达到Ffmax时，对应的运动量也达到了临界值.