专题　万有引力定律 题型分析

专题一 太阳与行星间的引力

例1　把行星运动近似看做匀速圆周运动以后，开普勒第三定律可写为T²＝，m为行星质量，则可推得(　　)

A．行星受太阳的引力为F＝k

B．行星受太阳的引力都相同

C．行星受太阳的引力为F＝k

D．质量越大的行星受太阳的引力一定越大

解析　行星受到的太阳的引力提供行星绕太阳做匀速圆周运动的向心力，则有F＝m，又因为v＝，代入上式得F＝.由开普勒第三定律＝k，得T²＝，代入上式得F＝k.太阳与行星间的引力与太阳、行星的质量及太阳与行星间的距离有关．故选C.

答案　C

专题二 万有引力定律公式的计算

例2　有一质量为M、半径为R、密度均匀的球体，在距离球心O为2R的地方有一质量为m的质点，现在从M中挖去一半径为的球体，如图所示，求剩下部分对m的万有引力F为多大？

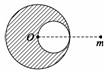
解析　仔细观察球体挖去部分及完整球体的形状特点，可知，完整部分与质点m以及挖去部分与质点m间万有引力均可用公式计算，由此联想到利用等割补的方式先将剩余部分还原为完整体，计算出万有引力，然后计算出割去部分与质点m间的万有引力，两者之差即为所求．

设想将被挖部分重新补回，则完整球体对质点m的引力为F₁，可以看作是剩余部分对质点的引力F与被挖小球对质点的引力F₂的合力，即F₁＝F＋F₂.

设被挖小球的质量为M′，其球心到质点间的距离为r′.

由题意，知M′＝，r′＝R

由万有引力定律，得F₁＝G＝

F₂＝G＝G＝

所以剩下部分对m的万有引力为F＝F₁－F₂＝.

答案　

归纳总结：对于此类问题，利用万有引力定律直接求解是不对的，当质点与质量分布均匀的球体间距离较小时，球体虽然不能被看作质点，但仍可用F＝G计算求解，此时的r应等于质点与球心间的距离．此题目中球体被挖，质量分布不均匀，要先“填补”变为质量分布均匀的球体再求解.

专题三 星球表面的重力加速度

例3　火星的质量和半径分别约为地球的和，地球表面的重力加速度为g，则火星表面的重力加速度约为(　　)

A．0.2g　　B．0.4g　　C．2.5g　　D．5g

解析：由星球表面的物体所受的重力近似等于万有引力知，对火星上的物体，m₁g′＝①

对地球上的物体，m₂g＝②

得＝＝＝0.4，则g′＝0.4g.

答案：B

归纳总结：(1)质量是物体本身的一种属性，它不随物体位置的变化而变化．

(2)火星表面的重力加速度与地球表面的重力加速度不同，故物体在火星表面的重力与在地球表面的重力不同．

(3)根据地球表面的重力加速度的表达式及火星表面的重力加速度的表达式，求出火星表面的重力加速度．

专题四 万有引力定律的综合问题

例4　要使两个物体之间的万有引力减小到原来的，可采用的方法是(　　)

A．使两物体之间的距离增至原来的2倍，质量保持不变

B．使两物体的质量各减少一半，距离保持不变

C．使其中一个物体的质量减为原来的，距离保持不变

D．使两物体的质量及它们之间的距离都减为原来的

解析　根据F＝G可知，当两物体质量不变，距离增至原来的2倍时，两物体间的万有引力F′＝＝·＝F，A正确；当两物体的距离保持不变，质量各减少一半时，万有引力F′＝＝×＝F，B正确；当只有一个物体的质量减为原来的时，万有引力F′＝＝·＝F，C正确；

当两物体的质量及它们之间的距离都减为原来的时，万有引力F′＝＝＝F，D错误．

答案　ABC

归纳总结：在利用万有引力定律与其他知识相联系的结合性问题中，注意分清过程，分别利用相关规律列方程，确定不同方程间相关联的物理量，解方程求得结果.