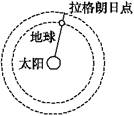
章末综合检测7     万有引力与宇宙航行

(时间：90分钟，满分：100分)

一、选择题(每小题5分，共60分)

1．对于万有引力定律的表达式F＝G，下列说法中正确的是(　　)

①公式中G为引力常量，它是由实验测得的，而不是人为规定的　②当r趋近于零时，万有引力趋于无穷大　③m₁与m₂受到的引力总是大小相等的，而与m₁、m₂是否相等无关

④m₁与m₂受到的引力是一对平衡力　⑤用该公式可求出任何两个物体之间的万有引力

A．①③⑤　　B．②④　　C．①②④　　D．①③

解析　公式中的G是卡文迪许通过实验测定的，不是人为规定的，故①正确；由于万有引力中的r是两个物体质心间的距离，所以当r趋于零时，两物体不可以再视作质点，公式在此时不适用，所以②错误；万有引力是两个物体间的相互作用，是一对作用力和反作用力，力的大小与两个物体质量是否相等无关，故③正确，④错误；万有引力普遍适用于任何可视为质点的两个物体之间的相互作用，故⑤错误．所以选D.

答案　D

2．下列关于地球同步通信卫星的说法中，正确的是(　　)

A．为避免同步通信卫星在轨道上相撞，应使它们运行在不同的轨道上

B．同步通信卫星定点在地球上空某处，各个同步通信卫星的角速度相同，但线速度可以不同

C．不同国家发射同步通信卫星的地点不同，这些卫星轨道不一定在同一平面内

D．同步通信卫星只能运行在赤道上空某一恒定高度上

解析　由于地球同步卫星的公转周期与地球自转周期相同，这就决定了地球同步卫星必须在赤道平面内，而且它的角速度、轨道半径、线速度等各个量是唯一确定的，与卫星的其他量无关．

答案　D

3．两个行星各有一个卫星绕其表面运行，已知两个卫星的周期之比为1∶2，两行星半径之比为2∶1，则下列选项正确的是(　　)

①两行星密度之比为4∶1　②两行星质量之比为16∶1　③两行星表面处重力加速度之比为8∶1　④两卫星的速率之比为4∶1

A．①②    B．①②③    C．②③④    D．①③④

解析　由T＝2π 、球体体积V＝πR³和质量公式M＝ρV，可知两卫星的轨道半径之比r₁∶r₂＝ ＝1∶2，且R₁∶R₂＝2∶1；故由v＝ 可得，v₁∶v₂＝4∶1；ρ₁∶ρ₂＝4∶1；g₁∶g₂＝8∶1.

答案　D

4．下列说法中正确的是(　　)

A．经典力学能够说明微观粒子的规律性

B．经典力学适用于宏观物体的低速运动问题，不适用于高速运动的问题

C．相对论与量子力学的出现，表示经典力学已失去意义

D．对于宏观物体的高速运动问题，经典力学仍能适用

解析　经典力学适用于低速宏观问题，不能说明微观粒子的规律性，不能用于宏观物体的高速运动问题．A、D错误，B正确. 相对论与量子力学的出现，并不否定经典力学，只是说经典力学有其适用范围，C错误．

答案　B

5．“嫦娥二号”成功进入了环绕“日地拉格朗日点”的轨道，我国成为世界上第三个造访该点的国家．如图所示，该拉格朗日点位于太阳和地球连线的延长线上，一飞行器处于该点，在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动，则此飞行器的(　　)

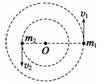
A．线速度大于地球的线速度

B．向心加速度大于地球的向心加速度

C．向心力仅由太阳的引力提供

D．向心力仅由地球的引力提供

解析 由于飞行器与地球同步绕太阳做圆周运动，则周期相同，根据v＝可知选项A正确；由a＝²r可知选项B正确；飞行器的向心力由地球和太阳的万有引力共同提供，选项C、D错误．

答案 AB

6．已知万有引力常量G，那么在下列给出的各种情景中，能根据测量的数据求出月球密度的是(　　)

A．在月球表面使一个小球做自由落体运动，测出落下的高度H和时间t

B．发射一颗贴近月球表面的绕月球做圆周运动的飞船，测出飞船运行的周期T

C．观察月球绕地球的圆周运动，测出月球的直径D和月球绕地球运行的周期T

D．发射一颗绕月球做圆周运动的卫星，测出卫星离月球表面的高度H和卫星的周期T

解析　根据选项A的条件可以算出月球上的重力加速度g，由g＝可以求出月球质量和月球半径的平方比＝，选项A不正确．根据选项B的条件，由＝m()²R可求出月球质量和月球半径的立方比＝，而月球密度为ρ＝＝＝，选项B正确．根据选项C的条件无法求出月球的质量，选项C不正确．根据选项D的条件，由＝m()²(R＋H)可求出＝，虽然知道H的大小，仍然无法求出月球质量和月球半径的立方比，故选项D也不正确．

答案　B

7．一宇宙飞船绕地心做半径为r的匀速圆周运动，飞船舱内有一质量为m的人站在可称体重的台秤上．用R表示地球的半径，g表示地球表面处的重力加速度，g′表示宇宙飞船所在处的地球引力加速度，FN表示人对台秤的压力，这些说法中，正确的是(　　)

A．g′＝0        B．g′＝g

C．FN＝0        D．FN＝mg

解析　由万有引力定律得G＝mg，G＝mg′，解得g′＝g，故选项B是正确的．因绕地球做匀速圆周运动的宇宙飞船处于完全失重状态，故选项C是正确的．

答案　BC

8．现代观测表明，由于引力作用，星体有“聚集”的特点．众多的恒星组成了不同层次的恒星系统，最简单的恒星系统是两颗互相绕转的双星．事实上，冥王星也是和另一星体构成双星，如图1所示，这两颗恒星m₁、m₂各以一定速率绕它们连线上某一中心O匀速转动，这样才不至于因万有引力作用而吸引在一起．现测出双星间的距离始终为L，且它们做匀速圆周运动的半径r₁与r₂之比为3∶2，则(　　)

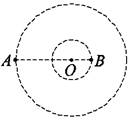
A．它们的角速度大小之比为2∶3

B．它们的线速度大小之比为3∶2

C．它们的质量之比为3∶2

D．它们的周期之比为2∶3

解析　双星的角速度和周期都相同，故A、D均错误．由＝m₁ω²r₁，＝m₂ω²r₂，解得m₁∶m₂＝r₂∶r₁＝2∶3，C错误．由v＝ωr知，v₁∶v₂＝r₁∶r₂＝3∶2，B正确．

答案　B

9．两个大小相同的实心均质小铁球，紧靠在一起时它们之间的万有引力为F；若两个半径2倍于小铁球的实心均匀大铁球紧靠在一起，则它们之间的万有引力为(　　)

A．2F  B．4F  C．8F  D．16F

解析　实心的密度均匀的球体紧靠在一起时，万有引力公式仍适用，故设小铁球半径为R，则两小铁球间：F＝G＝G＝Gπ²ρ²R⁴

同理，两大铁球之间F′＝G＝Gπ²ρ²(2R)⁴＝16F

故选项D正确．

答案　D

10．某星球的质量约为地球的9倍，半径约为地球半径的一半，若从地球表面高h处平抛一物体，射程为60 m，则在该星球上，从同样的高度以同样的初速度平抛同一物体，射程应为(　　)

A．10 m  B．15 m  C．90 m  D．360 m

解析　由平抛运动公式可知，射程x＝v₀t＝v₀，即v₀、h相同的条件下x∝，又由g＝，可得＝²＝ײ＝，所以＝ ＝，选项A正确．

答案　A

11．人造地球卫星绕地球做圆周运动，假如卫星的线速度减小到原来的，卫星仍做圆周运动，则(　　)

A．卫星的向心加速度减小到原来的

B．卫星的角速度减小到原来的

C．卫星的周期增大到原来的8倍

D．卫星的周期增大到原来的2倍

答案　C

12．我国绕月探测工程的预先研究和工程实施已取得重要进展．设地球、月球的质量分别为m₁、m₂，半径分别为R₁、R₂，人造地球卫星的第一宇宙速度为v，对应的环绕周期为T，则环绕月球表面附近圆轨道飞行的探测器的速度和周期分别为(　　)

A. v, T

B.  v, T

C.  v, T

D. v, T

解析 由向心力公式＝，＝，两式联立，得v₂＝ v；由T₂＝，T＝，两式联立，得T₂＝ T，故A项正确．

答案 A

二、解答题(每题10分，共40分)

13．我国在2008年10月24日发射了“嫦娥一号”探月卫星．同学们也对月球有了更多的关注．

(1)若已知地球半径为R，地球表面的重力加速度为g，月球绕地球运动的周期为T，月球绕地球的运动可近似看作匀速圆周运动，试求月球绕地球运动的轨道半径．

(2)若宇航员随登月飞船登陆月球后，在月球表面某处以速度v₀竖直向上抛出一个小球，经过时间t，小球落回抛出点．已知月球半径为r，万有引力常量为G，试求出月球的质量M_月．

解析　(1)根据万有引力定律和向心力公式

G＝M_月()²R′，mg＝G，解得R′＝

(2)设月球表面处的重力加速度为g_月，根据题意

v₀＝，g_月＝解得M_月＝

答案　(1)　(2)

14．我国成功发射“神舟七号”载人飞船．假设“神舟七号”载人飞船的舱中有一体重计，体重计上放一物体，火箭点火前，宇航员翟志刚观察到体重计显示对物体的弹力为F₀.在“神舟七号”载人飞船随火箭竖直向上匀加速升空的过程中，当飞船离地面高度为H时翟志刚观察到体重计显示对物体的弹力为F，设地球半径为R，第一宇宙速度为v，求：

(1)该物体的质量．

(2)火箭上升的加速度．

解析　(1)设地面附近重力加速度为g₀，由火箭点火前体重计示数为F₀，可知物体质量为m＝F₀/g₀

由第一宇宙速度公式v＝

可得地球表面附近的重力加速度g₀＝

联立解得该物体的质量为m＝

(2)当飞船离地面高度为H时，物体所受万有引力为F′＝G

而g₀＝GM/R²

对物体由牛顿第二定律得F－F′＝ma

联立以上各式解得火箭上升的加速度a＝－

答案　(1)　(2)－

15．如图所示，质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动，星球A和B两者中心之间距离为L.已知A、B的中心和O三点始终共线，A和B分别在O的两侧．引力常量为G.

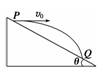
(1)求两星球做圆周运动的周期.

(2)在地月系统中，若忽略其他星球的影响，可以将月球和地球看成上述星球A和B，月球绕其轨道中心运行的周期记为T₁.但在近似处理问题时，常常认为月球是绕地心做圆周运动的，这样算得的运行周期为T₂.已知地球和月球的质量分别为5.98×10²⁴ kg和7.35×10²² kg，求T₂与T₁两者二次方之比(结果保留三位小数).

解析 (1)A、B绕O做匀速圆周运动，它们之间的万有引力提供向心力，所以A和B的向心力相等．且A、B和O始终共线，说明A和B有相同的角速度和周期.

因此有mω²r＝Mω²R，r＋R＝L

联立解得R＝ L，r＝ L

对A根据牛顿第二定律和万有引力定律得＝m²·L

化简得T＝2π .

(2)将地月看成双星，由(1)得T₁＝2π

将月球看做绕地心做圆周运动，根据牛顿第二定律和万有引力定律得＝m²L(2分)

整理得T₂＝2π

所以两周期的平方比值为²＝＝＝1.01.

答案 (1)2π 　(2)1.01

16．如图所示，宇航员站在某一质量分布均匀的星球表面一斜坡上的P点沿水平方向以初速度v₀抛出一个小球，测得小球经时间t落到斜坡上另一点Q，斜面的倾角为θ，已知该星球半径为R，万有引力常量为G，求：

(1)该星球表面的重力加速度g.

(2)该星球的第一宇宙速度v.

(3)人造卫星在该星球表面做匀速圆周运动的最小周期T.

解析　(1)小球做平抛运动，水平位移x＝v₀t

竖直位移y＝gt²

由位移关系得tan θ＝＝

g＝

(2)该星球的近地卫星的向心力由万有引力提供＝m①

该星球表面物体所受重力等于万有引力＝mg②

由①②得v＝ ＝

(3)人造卫星的向心力由万有引力提供＝mr，T＝ ＝

当r＝R时，T最小．

T＝ ＝ ＝ .

答案　(1)　(2) 　(3)