|
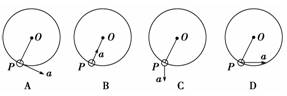
章末综合检测6 圆周运动 (时间:90分钟,满分:100分) 一、选择题(每小题5分,共60分) 1.如图所示,细绳的一端固定,另一端系一小球,让小球在竖直面内做圆周运动,关于小球运动到P点时的加速度方向,下列图中可能的是( )
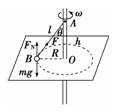
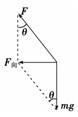
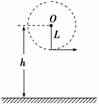
解析 竖直面内做圆周运动的小球在P点受到重力和绳拉力的共同作用,由牛顿第二定律可知其加速度a的方向即为所受二力合力的方向,且指向圆周的内侧,故A、B、C错误,D正确. 答案 D. 2.火车在转弯时,受向心力的作用,对其所受向心力的分析,正确的是( ) A.由于火车本身作用而产生了向心力 B.主要是由于内、外轨的高度差的作用,车身略有倾斜,车身所受重力的分力产生了向心力 C.火车在转弯时的速率小于规定速率时,内轨将给火车侧压力,侧压力就是向心力 D.火车在转弯时的速率大于规定速率时,外轨将给火车侧压力,侧压力作为火车转弯时向心力的一部分 解析 火车正常转弯时,重力和支持力的合力提供向心力,故A、B错;转弯速率大于(或小于)标准速率时,外轨(或内轨)有侧压力作用,此时火车受重力、支持力、侧压力的作用,三力合力提供向心力. 答案 D 3.在一个光滑水平面上,有一转轴垂直于此平面,交点O的上方h处固定一细绳的一端,绳的另一端固定一质量为m的小球B,绳长AB=l>h,小球可随转轴转动并在光滑水平面上做匀速圆周运动,要使球不离开水平面,转轴的转速最大值是( )
A. B.π C. D.2π 解析 以小球为研究对象,进行受力分析,如图所示,小球受三个力作用.重力mg、水平面支持力FN、绳子拉力F.在竖直方向上合
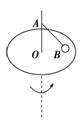
答案 A 4.A、B两个质点分别做匀速圆周运动,在相同时间内它们通过的路程比sA∶sB=2∶3,转过的角度比φA∶φB=3∶2,则下列说法中正确的是( ) A.它们的周期比TA∶TB=2∶3 B.它们的周期比TA∶TB=3∶2 C.它们的向心加速度大小比aA∶aB=4∶9 D.它们的向心加速度大小比aA∶aB=9∶4 解析 由v=得==,由ω=得==,则==,A正确、B错误;==×=1,C、D均不正确. 答案 A 5.如图所示,“旋转秋千”中的两个座椅A、B质量相等,通过相同长度的缆绳悬挂在旋转圆盘上.不考虑空气阻力的影响,当旋转圆盘绕竖直的中心轴匀速转动时,下列说法正确的是( )
A.A的速度比B的大 B.A与B的向心加速度大小相等 C.悬挂A、B的缆绳与竖直方向的夹角相等 D.悬挂A的缆绳所受的 解析 A、B绕竖直轴匀速转动的角速度相等,即ωA=ωB,但rA<rB,根据v=ωr得,A的速度比B的小,选项A错误;根据a=ω2r得,A的向心加速度比B的小,选项B错误;A、B做圆周运动时的受力情况如图所示,根据F向=mω2r及tan θ==知,悬挂A的缆绳与竖直方向的夹角小,选项C错误;由图知=cos θ,即F=,
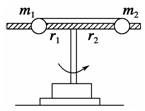
答案 D 6.如图所示,光滑杆上穿两个小球,用细绳把两球相连,当盘架匀速转动,两球恰能与杆保持相对静止,此时两小球到转轴的距离之比为2∶3,可知两小球质量m1与m2之比为( )
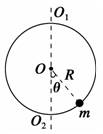
A.1∶2 B.2∶3 C.3∶2 D.∶ 解析 两球的角速度相等,且向心力均等于绳拉力,由m1r1ω2=m2r2ω2,知质量与转动半径成反比. 答案 C 7.一种玩具的结构如图所示,竖直放置的光滑圆环的半径为R=20 cm,环上有一穿孔的小球m,小球仅能沿环做无摩擦滑动.如果圆环绕着通过环心的竖直轴O1O2以10 rad/s的角速度旋转,则小球相对环静止时和环心O的连线与O1O2的夹角为(g取10 m/s2)( )
A.30° B.45° C.60° D.75° 解析 小球受到重力mg和圆环的支持力FN两个力的作用,两个力的合力提供向心力,根据牛顿第二定律有mgtan θ=mω2r,又r=Rsin θ,所以cos θ==,故θ=60°,选项C正确. 答案 C 8.一圆盘可绕通过圆盘的中心O且垂直于盘面的竖直轴转动,在圆盘上放置一小木块A,它随圆盘一起做减速圆周运动,如图2所示,则关于木块A的受力,下列说法正确的是( )
A.木块A受重力、支持力和向心力 B.木块A受重力、支持力和静摩擦力,摩擦力的方向与木块运动方向相反 C.木块A受重力、支持力和静摩擦力,摩擦力的方向不指向圆心 D.木块A受重力、支持力和静摩擦力,摩擦力的方向与木块运动方向相同 解析 由于圆盘上的木块A在竖直方向上没有加速度,所以,它在竖直方向上受重力和支持力作用而平衡;而木块在水平面内做减速圆周运动,其所需向心力由静摩擦力提供,又由于速度大小在减小,故静摩擦力还要提供它做减速运动的阻力,因此静摩擦力的方向不指向圆心. 答案 C 9.如图所示,有一个半径为R的光滑圆轨道,现给小球一个初速度,使小球在竖直面内做圆周运动,则关于小球在过最高点的速度v,下列叙述中正确的是( )
A.v的极小值为 B.v由零逐渐增大,轨道对球的弹力逐渐增大 C.当v由值逐渐增大时,轨道对小球的弹力也逐渐增大 D.当v由值逐渐减小时,轨道对小球的弹力逐渐增大 解析 因为轨道内壁下侧可以提供支持力,故最高点的最小速度可以为零.若在最高点v>0且较小时,球做圆周运动所需的向心力由球的重力跟轨道内壁下侧对球向上的力FN1的合力共同提供,即mg-FN1=m,当FN1=0时,v=,此时只有重力提供向心力.由此知,速度在0<v<时,轨道内壁下侧的弹力随速度的增大(减小)而减小(增大),故D正确.当v>时,球的向心力由重力跟轨道内壁上侧对球的向下的弹力FN2共同提供,即mg+FN2=m,当v由逐渐增大时,轨道内壁上侧对小球的弹力逐渐增大,故C项正确. 答案 10.如图所示,质量为m的木块从位于竖直平面内的圆弧形曲面上滑下,由于摩擦力的作用,木块从a到b运动的速率逐渐增大,从b到c运动的速率恰好保持不变,从c到d运动的速率逐渐减小,则( )
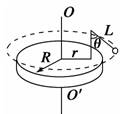
A.木块在ab段和cd段的加速度不为零,但在bc段的加速度为零 B.木块在ab、bc、cd各段中的加速度都不为零 C.木块在整个运动过程中所受的合外力大小一定,方向始终指向圆心 D.木块只在bc段所受的合外力大小不变,方向指向圆心 解析 木块从曲面上滑下做曲线运动,总有加速度,只有在做匀速圆周运动时,所受的合外力大小不变且方向指向圆心,故选项B、D正确. 答案 BD 11.如图所示,半径为R的圆盘绕过圆心的竖直轴OO′匀速转动,在距轴为r处有一竖直杆,杆上用长为L的细线悬挂一小球.当圆盘以角速度ω匀速转动时,小球也以同样的角速度做匀速圆周运动,这时细线与竖直方向夹角为θ,则小球的向心加速度大小为 ( )
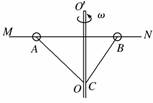
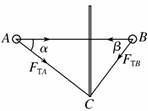
图2-13 A.ω2R B.ω2r C.ω2Lsin θ D.ω2(r+Lsin θ) 解析 小球运动的轨迹是水平面内的圆,如题图中虚线所示,其圆心是水平面与转轴OO′的交点,所以圆周运动的半径为r+L sin θ,再根据向心加速度公式a=ω2R得正确选项为D. 答案 D 12.如图所示,OO′为竖直转轴,MN为固定在OO′上的水平光滑杆,有两个质量相等的金属小球A、B套在水平杆上,AC和BC为抗拉能力相同的两根细绳,C端固定在OO′上,当线拉直时,A、B两球转动半径比值为2:1,当转轴角速度逐渐增大时( )
A.AC线先断 B.BC线先断 C.两绳同时断 D.不能确定哪个线先断 解析 两小球具有相同的角速度,线的拉力的水平分量提供小球做圆周运动的向心力,如图所示,则有
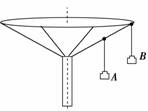
FTA·cosα=mrAω2,FTB·cosβ=mrBω2,==. 因为AC>BC,所以FTA>FTB,故AC线先断. 答案 A 二、解答题(每题10分,共40分) 13.如图所示,一个人用一根长1 m、只能承受74 N拉力的绳子,拴着一个质量为1 kg的小球,在竖直平面内做圆周运动,已知圆心O离地面h=6 m.转动中小球在最低点时绳子恰好断了.(取g=10 m/s2)
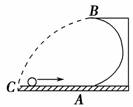
(1)绳子断时小 (2)绳断后,小球落地点与抛出点间的水平距离是多少? 解析 (1)设绳断时角速度为ω,则有F-mg=mω2L 代入数据得ω=8 rad/s. (2)绳断后,小球做平抛运动,其初速度v=ωL=8 m/s 由平抛运动规律有h-L=gt2 得t=1 s 水平距离x=vt=8 m. 答案 (1)8 rad/s (2)8 m 14.如图所示,一光滑的半径为R的半圆形轨道固定在水平面上,一个质量为m的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,对轨道的压力恰好为零,则小球落地点C距A处多远?
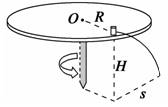
解析 小球在B点飞出时,对轨道压力为零,由mg=m,得vB=, 小球从B点飞出做平抛运动t= = , 水平方向的位移大小x=vBt=·=2R. 答案 2R 15.如图所示,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动.现测得转台半径R=0.5 m,离水平地面的高度H=0.8 m,物块平抛落地过程水平位移的大小s=0.4 m.设物块所受的最大静摩擦力等于滑动摩擦力,取重力加速度g=10 m/s2.求:
(1)物块做平抛运动的初速度大小v0; (2)物块与转台间的动摩擦因数μ. 解析 (1)物块做平抛运动,在竖直方向上有H=gt2① 在水平方向上有s=v0t② 由①②式解得v0=s③ 代入数据得v0=1 m/s. (2)物块离开转台时,最大静摩擦力提供向心力,有fm=m④ fm=μN=μmg⑤ 由④⑤式得μ= 代入数据得μ=0.2. 答案 (1)1 m/s (2)0.2 16.如图所示,半径为R,内径很小的光滑半圆管竖直放置.两个质量均为m的小球a、b以不同的速度进入管内,a通过最高点A时,对管壁上部的压力为3 mg,b通过最高点A时,对管壁下部的压力为0.75 mg,求a、b两球落地点间的距离.
解析 两个小球在最高点时,受重力和管壁的作用力,这两个力的合力提供向心力,离开轨道后两球均做平抛运动,a、b两球落地点离抛出点的水平距离为xa、xb.在A点,对a球:mg+3mg=,va= 对b球:mg-0.75 mg=m vb= 由平抛运动规律可得xa=vat=va =4R,xb=vbt=vb =R 故a、b两球落地点间的距离为:xa-xb=3R. 答案 3R |