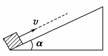
第八章  章末总结

要点归纳

知识点一、功

1．恒力的功可根据W＝Flcos α计算．

2．变力的功可转化为恒力的功，如图所示，

 

物体沿斜面上滑，然后又沿斜面滑回出发点的过程中，摩擦力是变力(方向变)，但若将过程分为两个阶段：上滑过程和下滑过程，则每个阶段摩擦力都是恒力，可由W＝Flcos α确定，然后求代数和，即为全过程摩擦力的功．

3．根据W＝Pt计算某段时间内的功．如机车以恒定功率启动时，牵引力是变力，但其做功快慢(P)是不变的，故t时间内的功为Pt.

4．利用动能定理W_合＝ΔEk计算总功或某个力的功，特别是变力的功．

5．由功能关系确定功，功是能量转化的量度，有多少能量发生了转化，就应有力做了多少功．

6．微元求和法．

知识点二、功率

1．P＝，此式求出的是t时间内的平均功率，当然若功率一直不变，亦为瞬时功率．

2．P＝Fv·cos α，即功率等于力F、运动的速度v以及力和速度的夹角α的余弦的乘积．

当α＝0时，公式简化为P＝F·v.

3．机车以恒定功率启动或以恒定加速度启动

(1)P＝Fv指的是牵引力的瞬时功率．

(2)依据P＝Fv及a＝讨论各相关量的变化，最终状态时三个量的特点：P＝Pm，a＝0(F＝Ff)，v＝vm.

知识点三、动能定理

1.对动能定理的理解

    (1)W总＝W1＋W2＋W3＋…，是包含重力在内的所有力做功的代数和，若合外力为恒力，也可这样计算：W总＝F合l cos α.

    (2)动能定理是计算物体位移或速率的简捷公式，当题目中涉及位移时可优先考虑动能定理．

(3)做功的过程是能量转化的过程，动能定理表达式中的“＝”的意义是一种因果联系的数值上相等的符号，它并不意味着“功就是动能增量”，也不意味着“功转变成了动能”，而是意味着“功引起物体动能的变化”．

(4)动能定理公式两边每一项都是标量，因此动能定理是一个标量方程．

知识点四、机械能守恒定律

1．判断机械能是否守恒的方法

(1)方法一：用做功来判定——对某一系统，若只有重力和系统内弹力做功，其他力不做功，则该系统机械能守恒．

(2)方法二：用能量转化来判定——若物体系统中只有动能和势能的相互转化而无机械能与其他形式的能的转化，则物体系统机械能守恒．

2．机械能守恒定律的表达式

(1)E₁＝E₂　系统原来的机械能等于系统后来的机械能．

(2)ΔEk＋ΔEp＝0　系统变化的动能与系统变化的势能之和为零．

(3)ΔE_A增＝ΔE_B减　系统内A物体增加的机械能等于B物体减少的机械能．

第一种表达式是从“守恒”的角度反映机械能守恒，解题时必须选取零势能面，而后两种表达式都是从“转化”的角度来反映机械能守恒，不必选取零势能面．

3．机械能守恒定律应用的思路

(1)根据要求的物理量，确定研究对象和研究过程．

(2)分析外力和内力的做功情况或能量转化情况，确定机械能守恒．

(3)选取参考面，表示出初、末状态的机械能．

(4)列出机械能守恒定律方程及相关辅助方程．

(5)求出未知量.

典例分析

一、动能定理

例1 如图所示，质量为m的小物块在粗糙水平桌面上做直线运动，经距离l后以速度v飞离桌面，最终落在水平地面上．已知l＝1.4 m，v＝3.0 m/s，m＝0.10 kg，物块与桌面间的动摩擦因数μ＝0.25，桌面高h＝0.45 m．不计空气阻力，重力加速度g取10 m/s2.求：

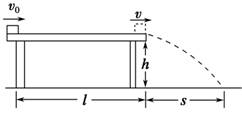
(1)小物块落地点距飞出点的水平距离s；

(2)小物块落地时的动能Ek；

(3)小物块的初速度大小v0.

解析　(1)小物块飞离桌面后做平抛运动，根据平抛运动规律，有

竖直方向：h＝gt²

水平方向：s＝vt

解得水平距离s＝v＝0.90 m.

(2)小物块从飞离桌面到落地的过程中机械能守恒，根据机械能守恒定律可得小物块落地时的动能为

E_k＝mv²＋mgh＝0.90 J.

(3)小物块在桌面上运动的过程中，根据动能定理，有

－μmgl＝mv²－mv

解得小物块的初速度大小v₀＝＝4.0 m/s.

答案　(1)0.90 m　(2)0.90 J　(3)4.0 m/s

二、变力功的求解

例2 如图所示，质量为m的物体用细绳经过光滑小孔牵引在光滑水平面上做匀速圆周运动，拉力为某个值F时，转动半径为R，当拉力逐渐减小到时，物体仍做匀速圆周运动，半径为2R，则外力对物体所做的功大小是(　　)

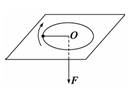
A.　　　B.　　　C.　　　D．零

解析　设当绳的拉力为F时，小球做匀速圆周运动的线速度为v₁，则有F＝

当绳的拉力减为时，小球做匀速圆周运动的线速度为v₂，则有F＝m

在绳的拉力由F减为F的过程中，绳的拉力所做的功为

W＝mv－mv＝－FR

所以，绳的拉力所做的功的大小为FR，A选项正确．

答案　A

归纳总结：该题中绳的拉力显然是变力，当求变力所做的功时，可以用动能定理求解.

三、摩擦力做功的求解

例3 如图所示，滑块以速率v₁靠惯性沿固定斜面由底端向上运动，当它回到出发点时速率变为v₂，且v₂＜v₁，若滑块向上运动的位移中点为A，取斜面底端重力势能为零，则(　　)

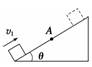
A．上升时机械能减小，下降时机械能增大

B．上升时机械能减小，下降时机械能也减小

C．上升过程中动能和势能相等的位置在A点上方

D．上升过程中动能和势能相等的位置在A点下方

解析　设A点的高度为h，斜面的倾角为θ，物体与斜面间动摩擦因数为μ，从开始到上升到最高点过程中，由动能定理得

mv＝mg2h＋μmgcosθ＝mg2h＋μmg2hcot θ

解得h＝

设滑块在B点时动能与势能相等，高度为h′，则有

mgh′＝mv－mgh′－μmgcos θ

解得h′＝，所以h′>h.

物体在斜面上无论上升还是下降，摩擦力皆做负功，摩擦生热，机械能减少．

答案　BC

四、关于功率的问题

例4 汽车发动机的额定功率为Pm＝60 kW，汽车质量为m＝5 t，运动时与地面间的动摩擦因数μ＝0.1.求：

(1)汽车所能达到的最大速度vm.

(2)若汽车以a＝0.5 m/s²的加速度由静止开始做匀加速直线运动．这一过程能维持多长时间？(g＝10 m/s²)

(3)当速度v₁＝4 m/s时，汽车的加速度a₁是多大？功率P₁是多大？

(4)当速度v₂＝10 m/s时，汽车的加速度a₂是多大？功率P₂是多大？

解析　(1)当汽车达到最大速度vm时，a＝0，牵引力F等于阻力Ff，Ff＝μmg，再由Pm＝F·vm得最大速度大小为vm＝＝

＝ m/s＝12 m/s

(2)汽车从静止开始匀加速启动，牵引力F恒定且由F－Ff＝ma，得F＝Ff＋ma＝μmg＋ma

由于速度不断增大，因此发动机功率P也不断增大(因P＝Fv ∝v)，当功率增至额定功率Pm时，匀加速运动结束，其匀加速运动阶段的最大速度为

v′＝＝＝ m/s＝8 m/s

故可知匀加速运动维持的时间为t′＝＝ s＝16 s

(3)由于速度v₁＝4 m/s＜v′，因此汽车仍处于匀加速运动阶段，故加速度a₁＝a＝＝ m/s²＝0.5 m/s²

功率P₁＝Fv₁＝(Ff＋ma)v₁＝(0.1×5×10³×10＋5×10³×0.5)×4 W＝3×10⁴ W

(4)由于速度v₂＝10 m/s＞v′且v₂＜vm，因此汽车做变加速运动，其功率P₂＝Pm＝60 kW，由P₂＝F₂v₂得牵引力

F₂＝＝ N＝6×10³ N

加速度a₂＝＝ m/s²＝0.2 m/s²

答案　(1)12 m/s　(2)16 s　(3)0.5 m/s²　3×10⁴ W (4)0.2 m/s²　60 kW

五、功能关系的应用

例5 如图所示，在水平桌面的边角处有一轻质光滑的定滑轮K，一条不可伸长的轻绳绕过K分别与物块A、B相连，A、B的质量分别为m_A、m_B.开始时系统处于静止状态，现用一水平恒力F拉物块A，使物块B上升．已知当B上升距离为h时，B的速度为v.求此过程中物块A克服摩擦力所做的功．(重力加速度为g)

 

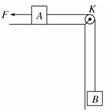
解析　在此过程中，B的重力势能的增量为m_Bgh，A、B动能的增量为(m_A＋m_B)v²，恒力F所做的功为Fh，用W表示物体A克服摩擦力所做的功，根据功能关系有

Fh－W＝(m_A＋m_B)v²＋m_Bgh

即W＝Fh－(m_A＋m_B)v²－m_Bgh

答案　Fh－(m_A＋m_B)v²－m_Bgh

六、传送带问题

例6　如图所示，水平传送带AB的右端与竖直面内的光滑半圆形轨道DC相接．传送带的运行速度为v₀＝8 m/s，将质量m＝1.0 kg的滑块无初速度地放到传送带A端．已知传送带长度L＝12.0 m，竖直面内的光滑半圆形轨道的半径R＝0.8 m，滑块与传送带间的动摩擦因数为μ＝0.4，重力加速度g＝10 m/s².试求：

  

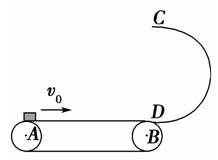
(1)滑块从传送带A端运动到B端所需的时间；

(2)滑块在传送带上滑行的整个过程中产生的热量；

(3)滑块滑到轨道最高点C时对轨道的压力．

解析　(1)滑块在传送带上做加速运动的加速度a＝μg＝4 m/s²

加速到与传送带同速所用时间t₁＝＝2 s

位移x₁＝at＝8 m＜12 m，因此滑块在传送带上先做加速运动，后做匀速运动，做匀速运动的位移x₂＝L－x₁＝4 m

所用时间t₂＝＝0.5 s

故t＝t₁＋t₂＝2.5 s.

(2)在t₁时间内，传送带的位移x′＝v₀t₁＝16 m

故Q＝fΔx＝μmg(x′－x₁)＝32 J.

(3)滑块由D到C过程中机械能守恒，则

mg(2R)＋mv＝mv

在C点，轨道对滑块的弹力与滑块重力的合力提供向心力

则N＋mg＝，解得N＝30 N.

由牛顿第三定律得滑块对轨道的压力N′＝N＝30 N，方向竖直向上．

答案　见解析

七、动能定理和机械能守恒定律的综合应用

例7　如图所示，摩托车运动员从高度h＝5 m的高台上水平飞出，跨越L＝10 m的壕沟．摩托车以初速度v₀从坡底冲上高台的过程历时t＝5 s，发动机的功率恒为P＝1.8 kW.已知人和车的总质量为m＝180 kg(可视为质点)，忽略一切阻力．取g＝10 m/s².

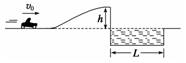
(1)要使摩托车运动员从高台水平飞出刚好越过壕沟，求他离开高台时的速度大小．

(2)欲使摩托车运动员能够飞越壕沟，其初速度v₀至少应为多大？

(3)为了保证摩托车运动员的安全，规定飞越壕沟后摩托车着地时的速度不得超过26 m/s，那么，摩托车飞离高台时的最大速度vm应为多少？

解析　(1)摩托车运动员由高台水平飞出后由平抛运动规律：水平方向：L＝v_ht①

竖直方向：h＝gt²②

联立①②得v_h＝10 m/s

(2)摩托车运动员由坡底冲上高台，根据动能定理

Pt－mgh＝mv－mv③

将v_h＝10 m/s代入到③得v₀＝10 m/s

(3)从高台水平飞出到地面，由机械能守恒定律

mvm²＋mgh＝mv

解得vm＝24 m/s

答案　(1)10 m/s　(2)10 m/s　(3)24 m/s