第八章　机械能守恒定律

第1节　功与功率

知识点归纳

知识点一、功

1．功的定义：如果一个物体受到力的作用，并且在力的方向上发生了位移，我们就说这个力对物体做了功．

2．功的两个要素：

(1) 力；

(2)物体在力的方向上发生了位移．

3．功的计算式：W＝Flcos α

力对物体所做的功等于力F的大小、位移l的大小、力与位移的夹角α的余弦这三者的乘积，即W＝Flcosα .

4．功的单位：在国际单位制中，功的单位是焦耳，简称焦，符号是J.1 J等于1 N的力使物体在力的方向上发生1 m的位移时所做的功，即1 J＝1 N·m.

5．功的方向性：功是标量，只有大小，没有方向．

6．功的物理意义：功是描述力在空间位移上累积作用的物理量，是能量转化的量度．

知识点二、正功和负功

1．功是标量，但有正、负之分，正负号不表示方向，只表示力的作用效果．

2．对公式中 α角的理解.

1．正功与负功的判断

①当0≤α<，F＝F₁与l方向的夹角小于90°，F₁有利于物体运动，W＝F₁lcos α，cos α>0，W>0，F₁对物体做正功．

②当<α≤π，F＝F₂与l方向的夹角大于90°，F₂阻碍物体运动，W＝F₂lcos α，cos α<0，W<0，F₂对物体做负功．

③当α＝时，cos α＝0，W＝0，F与l垂直，F在l方向上对物体不做功．

知识点三、总功的计算

当一个物体在几个力的共同作用下发生一段位移时，计算这几个力对物体所做的总功，通常有以下两种方法：

1．这几个力对物体所做的总功等于各个力分别对物体所做的功的代数和．

若以W1、W2、W3…分别表示力F1、F2、F3…所做的功，则这些力所做的总功为W总＝W1＋W2＋W3＋…(负功连同负号一起代入计算)．

2．这几个力对物体所做的总功等于这几个力的合力对物体所做的功．若以F合表示这几个力的合力，则这些力所做的总功为W总＝F合lcosα.

3．变力功的计算

(1)将变力的功转化为恒力的功．

①题目中明确指出是平均力，如一小球从高处掉下，落入泥土深度为l，泥土对小球的平均阻力为F阻，则泥土对小球的平均阻力所做的功W＝－F阻l.

②当力的方向不变，大小随位移按照线性规律变化时可先求出力对位移的平均值＝，再由W＝Flcos α计算功，如弹簧弹力做的功．

(2)力F在全程中是变力，但在每一个阶段是恒力，这样就可以先计算每个阶段的功，再利用求和的方法计算整个过程中变力做的功．

(3)阻力的功及图象法．

①阻力的功：如果阻力大小不变，方向始终与运动方向相反，可以直接用力的大小乘以路程．如滑动摩擦力、空气阻力做功等．

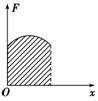
②图象法，如图所示，在F－x图象中，如果能求出图线与x轴围成的面积，这个面积值，即为F在这段位移上的功．

知识点四、功率

1．定义： 一个力所做的功W跟完成这些功所用的时间t的比值叫做功率，通常用P表示．

2．定义式：根据功率的定义，可知P＝.

3．单位：在国际单位制中，功率的单位是瓦特，简称瓦，符号是W．常用单位：1 kW＝103W.

4．标矢性：功率是标量，只有大小，没有方向，但有正负．功率的正负的意义与功的正负的意义相同．

5．物理意义：功率是表征物体做功快慢的物理量，它由物体做的功与做这些功所用的时间共同决定，并不单纯由做功的多少决定．只有在做功时间相同的情况下，才能认为物体做的功越多，功率越大．

知识点五、平均功率和瞬时功率

1．平均功率：表示在一段时间内做功的平均快慢，用公式表示成P＝或P＝.

2．瞬时功率：表示在某一位置 (或某一时刻)做功的快慢，一般用P＝Fv来求．

知识点六、额定功率和实际功率

1．额定功率是发动机正常工作时的最大功率，通常都在铭牌上标明．额定功率是动力机器重要的性能指标，一个动力机器的额定功率是一定的．

2．实际功率是发动机实际工作时输出的功率．机器工作时都要受额定功率的限制，发动机实际工作时输出的功率(即实际功率)，可以小于或等于额定功率，有时实际功率也会略大于额定功率，但不允许长时间超过额定功率．

知识点七、功率与速度

由公式P＝Fv知：

1．P一定时，F与v成反比．2．v一定时，P与F成正比．

3．F一定时，P与v成正比．

知识点八、功率的计算

1．P＝是功率的定义式，物理学中有许多物理量是用“比值”来定义的，如前面学习的速度、加速度等．若t较长，P为平均功率．只有在趋向于零时，P才视为瞬时功率，可见P＝只能计算平均功率．

2．公式P＝Fv是功率的另一种计算方法．当V是平均速度时，对应平均功率，当V是瞬时速度时对应瞬时功率．

3．平均功率和瞬时功率的计算．

(1)平均功率的计算

①由于平均功率描述了物体在一段时间内做功的快慢程度，它和一段时间(或一个过程)相对应，可直接用功率的定义式进行计算，＝W/t.

②当恒力做功时W＝Flcosα，则恒力对应的功率为P＝Fv cosα，当v是运动物体在某一段时间内的平均速度时，P就是对应该段时间内的平均功率，即P＝F    cosα.

应当注意的是，平均功率总是与某段时间(或某一过程)相对应，所以对于平均功率一定要明确是哪段时间(或哪一过程)内的．

(2)瞬时功率的计算

①由功率的定义式P＝，某一时刻t的瞬时功率等于包含t时刻在内的一段无限小的时间Δt内所做的功ΔW与这段时间的比，即P＝，但实际上这样计算是不方便的．

②通常情况下，计算瞬时功率可根据P＝Fvcos α求出，其中v是瞬时速度，α为F与v之间的夹角，P、F、v、α为瞬时对应关系．

知识点八、机车的启动问题

 

典例分析

一、功的公式W＝Flcos α的基本应用

例1 质量m＝3 kg的物体，受到与斜面平行向下的拉力F＝10 N，沿固定斜面下滑距离 l＝2 m．斜面倾角θ＝30°，物体与斜面间的动摩擦因数μ＝.求各力对物体所做的功，以及力对物体所做的总功．(g 取10 m/s2)

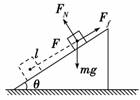
解析 如图所示，物体受到重力、拉力、斜面的支持力和摩擦力的作用，做单向直线运动，其位移的大小与移动的距离相等．所以重力所做的功为

WG＝mglcos(90°－θ)＝3×10×2×cos 60°J＝30 J，

拉力所做的功WF＝Fl＝10×2 J＝20 J.

支持力与物体运动方向垂直，它所做的功WFN＝0.滑动摩擦力的方向与位移方向相反，做功为WFf＝－(μmgcos θ)l＝－×3×10××2 J＝－30 J.

总功W＝WG＋WF＋WFN＋WFf＝30 J＋20 J＋(－30) J＝  20 J.

答案：WG＝30 J　WF＝20 J　WFN＝0　WFf＝－30 J　 W总＝20 J

归纳总结：求力的功，首先对物体受力分析，明确求哪个力的功，如果此力是恒力，可应用W＝Flcos α求功.

二、有关摩擦力的功的计算

例2 静止在光滑水平面上的物体质量为2.5 kg，在与水平方向成60°角斜向上的力F作用下运动了10 s，已知F＝10 N，求10 s内力F所做的功．(g 取10 m/s2)

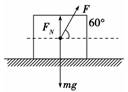
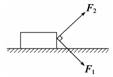
解析 物体受力如图所示．力F在竖直方向的分力显然小于重力，物体沿光滑水平面运动，根据牛顿第二定律Fcos 60°＝ma①

10 s内物体的位移大小l＝at²②

10 s内力F所做的功W＝Flcos 60° ③

由①②③得W＝＝500 J.

答案 500 J

归纳总结：1．摩擦力做功可以是正，也可以是负，也可以是零．

2．在传送带上分析摩擦力做的功，有可能出现两种情况：一种情况是物体在传送带上一直加速运动，另一种情况是物体在传送带上先加速，后匀速，匀速时不受摩擦力作用.

三、变力做功问题

例3 如图所示，摆球质量为m，悬线的长为l，把悬线拉到水平位置后放手．设在摆球运动过程中空气阻力Ff的大小不变，求摆球从A运动到竖直位置B时，重力mg、绳的拉力FT、空气阻力Ff各做了多少功？

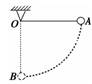
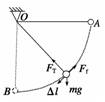
解析　因为拉力FT在运动过程中，始终与运动方向垂直，故不做功，即WF_T＝0.

重力在整个运动过程中始终不变，小球在重力方向上的位移为AB在竖直方向上的投影OB，且OB＝l，所以WG＝mgl.

空气阻力虽然大小不变，但方向不断改变，且任何时刻都与运动方向相反，即沿圆弧的切线方向，因此属于变力做功问题．如果将分成许多小弧段，使每一小段弧小到可以看成直线，在每一小段弧上Ff的大小、方向可以认为不变(即为恒力)，这样就把变力做功的问题转化为恒力做功的问题，如右图所示．因此Ff所做的总功等于每一小段弧上Ff所做功的代数和．即

WF_f＝－(FfΔl₁＋FfΔl₂＋…)＝－Ffπl

故重力mg做的功为mgl，绳子拉力FT做功为零，空气阻力Ff做的功为－Ffπl.

答案　WF_T＝0，WG＝mgl，WF_f＝－Ffπl

归纳总结：1．求变力做功有微元法，图象法，有时可通过转换研究对象，转换为恒力的功来计算．

2．滑动摩擦力、空气阻力总与物体相对运动的方向相反，物体做曲线运动时，可把运动过程细分，其中每一小段做功为Fl，整个过程中所做的功是力与各小段位移大小之积的和.

四、功率的计算

例4 质量为m的物体静止在光滑水平面上，从t＝0时刻开始受到水平力的作用．力的大小F与时间t的关系如图所示，力的方向保持不变，则(　　)

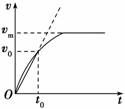
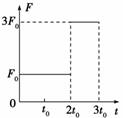
A．3t₀时刻的瞬时功率为

B．3t₀时刻的瞬时功率为

C．在t＝0到3t₀这段时间内，水平力的平均功率为

D．在t＝0到3t₀这段时间内，水平力的平均功率为

解析 0～2t₀时间内，物体的加速度a₁＝，位移s₁＝ a₁(2t₀)²＝，2t₀时刻的速度v₁＝a₁·2t₀＝；2t₀～3t₀时间内，物体的加速度a₂＝，位移s₂＝v₁t₀＋a₂t＝，3t₀时刻的速度v₂＝v₁＋a₂t₀＝.所以3t₀时刻的瞬时功率   P＝3F₀v₂＝，选项A错误，B正确；0～3t₀时间内的平均功率＝＝＝，选项C错误，D正确．

答案 BD

归纳总结：1．求功率首先明确求的是平均功率还是瞬时功率．

2．求平均功率的方法可用P＝或P＝Fv(v为平均速度)；求瞬时功率只可用P＝Fv(v为瞬时速度).

五、有关功率和速度的问题

例5 在一次抗洪抢险活动中，解放军某部队用直升机抢救一重要落水物体，静止在空中的直升机上的电动机通过吊绳将物体从直升机正下方90 m处的洪水中吊到机舱里．已知物体的质量为80 kg，吊绳的拉力不能超过1 200 N，电动机的最大输出功率为12 kW.为尽快把物体安全救起，操作人员采取的办法是，先让吊绳以最大拉力工作一段时间，而后电动机又以最大功率工作，当物体到达机舱前已达到最大速度．(g取10 m/s2)求：

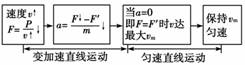
(1)物体匀加速运动的时间；

(2)物体运动的最大速度．

解析 (1)先让吊绳以最大拉力T_m＝1 200 N工作时，物体上升的加速度为a，由牛顿第二定律得a＝，代人数据得a＝5 m/s²

当吊绳拉力功率达到电动机最大功率P_m＝12 kW时，设物体速度为v，由P_m＝T_mv得

v＝＝ m/s＝10 m/s

物体匀加速运动的时间为t＝＝2 s

(2)此后电动机功率不变．当吊绳拉力T＝mg时，物体达到最大速度，则

vm＝＝＝15 m/s.

答案 (1)2 s　(2)15 m/s

归纳总结：1．由P＝Fv知三个物理量是相互制约的

(1)v一定：P∝F(2)P一定：F∝(3)F一定：P∝v

2．注意：平常所说的汽车、轮船等物体的功率是指牵引力的功率.

六、关于机车的启动分析

例5 汽车的质量为4×103 kg，额定功率为30 kW，运动中阻力大小恒为车重的0.1倍．汽车在水平路面上从静止开始以8×103 N的牵引力出发，求：(g＝10 m/s2)

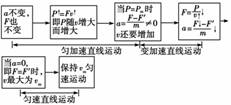
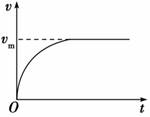
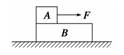
       (1)经过多长时间汽车达到额定功率？

       (2)汽车达到额定功率后保持功率不变，最大速度多大？

       (3)汽车加速度为0.6 m/s2时速度多大？

解析　(1)汽车运动的加速度为：

a＝＝(8×10³－0.1×4×10³×10)/4×10³ m/s²＝1 m/s²，

匀加速过程能达到的最大速度：v＝＝30××10³ m/s＝3.75 m/s.

匀加速过程持续的时间为：t＝＝ s＝3.75 s.

(2) v_m＝＝30× m/s＝7.5 m/s.

(3)汽车加速度为0.6 m/s²时的牵引力为：

F′－F_阻＝ma′，F′＝4×10³×0.6 N＋0.1×4×10³×10 N＝6.4×10³ N

此时汽车的功率为额定功率，所以汽车的速度：

v′＝＝30××10³ m/s＝4.7 m/s.

答案　(1)汽车经过3.75 s达到额定功率；(2)最大速度为7.5 m/s；(3)汽车加速度为0.6 m/s2时速度为4.7 m/s.

归纳总结：1．分析此类问题的两个工具

(1)P＝Fv.   (2)F－Ff＝ma.  由此分析P、F、v、a四个量的相互制约．

2．两个过程的共同点：当P＝P_额，a＝0时，到达最大速度vm＝＝.

自我检测

1．下列关于做功的说法中正确的是(　　)

A．凡是受力作用的物体，一定有力对物体做功

B．凡是发生了位移的物体，一定有力对物体做功

C．只要物体受力的同时又有位移发生，则一定有力对物体做功

D．只要物体受力，又在力的方向上发生位移，则力一定对物体做功

解析　做功有两个要素，第一要有力，第二在力的方向上物体要发生位移．A项错在物体可能没有发生位移，B项错在物体可能没受力，C项错在位移和力可能垂直，D项正确．

答案　D

2．如图所示，木块A放在木块B的左上端，用恒力F拉至B的右端，第一次将B固定在地面上，F做的功为W₁；第二次让B可以在光滑地面上自由滑动，F做的功为W₂，比较两次做功，可能是(　　)

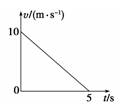
A．W₁<W₂             B．W₁＝W₂

C．W₁>W₂             D．无法比较

解析　若A、B间接触面光滑，则第二次即使B不固定，用水平力F拉木块A时，木块B也会静止，则W₁＝W₂；若A、B间接触面粗糙，则把A拉至B的右端时，A相对地面的位移大于第一种情况下的位移，所以W₁<W₂，应选A、B.

答案　AB

3．关于功率公式P＝和P＝Fv的说法正确的是(　　)

A．由P＝知，只要知道W和t就可求出任意时刻的功率

B．由P＝Fv只能求某一时刻的瞬时功率

C．从P＝Fv知汽车的功率与它的速度成正比

D．从P＝Fv知当汽车发动机功率一定时，牵引力与速度成反比

解析　P＝是对应一段时间内的功率，是平均功率，在P＝F·v中，若v为平均速度，则P为平均功率．若v为瞬时速度，则P为瞬时功率．当P一定时，F与v成反比．

答案　D

4．质量为m的汽车由静止开始以加速度a做匀加速运动，经过时间t，汽车达到额定功率，则下列说法正确的是(　　)

A．at即为汽车额定功率下的速度最大值

B．at还不是汽车额定功率下速度最大值

C．汽车的额定功率是ma²t

D．题中所给条件求不出汽车的额定功率

解析　汽车额定功率下的最大速度是a＝0时，vm＝＝，故A项错误，B项正确．汽车的功率是牵引力的功率，不是合力的功率，故C项错误．由F－Ff＝ma，F＝Ff＋ma，因Ff不知，则F不知，故求不出汽车的额定功率，故D项正确．

答案　BD

5．一质量为m的木块静止在光滑的水平面上，从t＝0开始，将一个大小为F的水平恒力作用在该木块上，在t＝t₁时刻力F的功率是(　　)

A.t₁　　　B.t　　　C.t₁　　　D.t

解析　题目所求t₁时刻的功率为瞬时功率．

物体的加速度a＝

t₁时刻的速度v₁＝at₁＝t₁

所以t₁时刻的功率P₁＝Fv₁＝t₁.

答案　C

6．质量是2 kg的物体置于水平面上，在运动方向上受拉力F作用沿水平面做匀变速运动，物体运动的速度—时间图象如图所示，若物体受摩擦力为10 N，则下列说法正确的是(　　)

A．拉力做功150 J

B．拉力做功100 J

C．摩擦力做功250 J

D．物体克服摩擦力做功250 J

解析　由图可知：a＝＝ m/s²＝2 m/s²，物体做匀减速运动，故Ff－F＝ma，F＝Ff－ma＝(10－2×2) N＝6 N，由图可知：l＝t＝×5 m＝25 m，故拉力做的功：WF＝Fl＝6×25 J＝150 J，摩擦力做的功WF_f＝－Ffl＝－10×25 J＝－250 J，故物体克服摩擦力做功250 J.

答案　AD

7．一汽车在水平公路上行驶，设汽车在行驶过程中所受阻力不变．汽车的发动机始终以额定功率输出，关于牵引力和汽车速度的下列说法中正确的是(　　)

A．汽车加速行驶时，牵引力不变，速度增大

B．汽车加速行驶时，牵引力增大，速度增大

C．汽车加速行驶时，牵引力减小，速度增大

D．当牵引力等于阻力时，速度达到最大值

解析　汽车的发动机输出功率恒定，即P一定，则由式P＝Fv可得：v增大，F减小，但由于合外力方向与汽车运动方向一致，因此汽车速度仍在增大，当汽车受到的牵引力和阻力相等时，汽车速度达到最大值，而后进行匀速运动，故选C、D.

答案　CD

8．质量为m的物体沿直线运动，只受到一个力F的作用．物体的位移l、速度v、加速度a和F对物体做功功率P随时间变化的图象如图所示，其中不可能的是(　　)

  

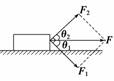
解析　在力F作用下物体做匀变速运动，所以C正确；v应该均匀增加，所以B错；l增加越来越快，所以A错；P＝Fv＝t，所以D正确．

答案　AB

9．质量为m，发动机的额定功率为P₀的汽车沿平直公路行驶，当它的加速度为a时，速度为v，测得发动机的实际功率为P₁，假设运动中所受阻力恒定，则它在平直公路上匀速行驶的最大速度是(　　)

A．v                   B.

C.              D.

解析　当加速度为a时，有F＝Ff＋ma＝，得阻力Ff＝－ma.当F＝Ff时，速度最大为v_max，则v_max＝＝，故选C.

答案　C

10．如图所示，在光滑水平面上，物体受两个相互垂直的大小分别为F₁＝3 N和F₂＝4 N的恒力，其合力在水平方向上，从静止开始运动10 m，求：

(1)F₁和F₂分别对物体做的功是多少？代数和为多大？

(2)F₁和F₂合力为多大？合力做功是多少？

解析　(1)力F₁做的功W₁＝F₁lcos θ₁＝3×10×cos 53° J＝18 J

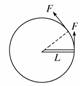
力F₂做的功W₂＝F₂lcos θ₂＝4×10×cos 37° J＝32 J

W₁与W₂的代数和W＝W₁＋W₂＝18 J＋32 J＝50 J

(2)F₁与F₂的合力F＝＝ N＝5 N

合力F做的功W′＝Fl＝5×10 J＝50 J

答案　(1)18 J　32 J　50 J　(2)5 N　50 J

11．如图所示，磨杆长为L，在杆端施以与杆垂直且大小不变的力F，求杆绕轴转动一周的过程中力F所做的功．

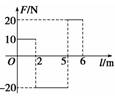
解析　磨杆绕轴转动过程中，力的方向不断变化，不能直接用公式W＝Flcos α进行计算．这时，必须把整个圆周分成许多小弧段，使每一小段弧都可以看作是这段弧的切线即可以看成是这段的位移，这样，由于F的大小不变，加之与速度的方向相同，因而对于每一小段圆弧均可视为恒力做功．杆绕轴转动一周所做功的总和为

W＝W₁＋W₂＋…＋W_n＝F·Δl₁＋F·Δl₂＋…＋F·Δl_n

因为Δl₁＋Δl₂＋…＋Δl_n＝2πL

所以W＝F·2πL.

答案　F·2πL

12．如图所示，是一个物体受到的力F与位移l的关系图象，由图象求力F对物体所做的功．

解析　F—l的面积表示F做的功：0～2 m内：W₁＝20 J；2 m～5 m：W₂＝－60 J；5 m～6 m：W₂＝20 J，故整个过程W＝W₁＋W₂＋W₃＝－20 J.

答案　－20 J

13．将一质量为m的物体从离地面h处，以速度v₀水平抛出，求物体从抛出到落地过程中重力的功率和在物体刚要落地时重力的功率(不计空气阻力)．

解析　平抛运动过程中重力做的功为W＝mgh

平抛运动的时间t＝

从抛出到落地过程中重力的(平均)功率为P＝＝＝mg

物体刚要落地时竖直分速度为v_y＝gt＝.

刚要落地时重力的功率为P′＝mgv_y＝mg.

答案　mg 　mg

14．修建高层建筑常用塔式起重机．在起重机将质量m＝5×10³kg的重物竖直吊起的过程中，重物由静止开始向上做匀加速直线运动，加速度a＝0.2m/s²，当起重机输出功率达到其允许的最大值时，保持该功率直到重物做v_m＝1.02m/s的匀速运动．取g＝ 10m/s²，不计额外功．求：

(1)起重机允许输出的最大功率；

(2)重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率．

解析　(1)设起重机允许输出的最大功率为P₀，重物达到最大速度时，拉力F₀等于重力．

P₀＝F₀v_m                                                                                                                ①

F₀＝mg                                                           ②

代入数据，得P₀＝5.1×10⁴ W                         ③

(2)匀加速运动结束时，起重机达到允许输出的最大功率，设此时重物受到的拉力为F，速度为v₁，匀加速运动经历的时间为t₁，有

P₀＝Fv₁                                                                                                                    ④

F－mg＝ma                                                    ⑤

v₁＝at₁                                                                                                                       ⑥

由③④⑤⑥，代入数据得t₁＝5 s                     ⑦

t＝2 s时，重物处于匀加速运动阶段，设此时速度为v₂，输出功率为P，则v₂＝at  ⑧

P＝Fv₂                                                                                                                      ⑨

由⑤⑧⑨，代入数据，得P＝2.04×10⁴ W.

答案　(1)5.1×10⁴ W   (2)5 s　2.04×10⁴ W