第七章  章末总结

要点归纳

知识点一、人造卫星的几个速度

1.发射速度：卫星直接从地面发射后离开地面时的速度，相当于在地面上用一门威力强大的大炮将卫星轰出炮口时的速度，发射卫星离开炮口后，不再有动力加速．

2．环绕速度(第一宇宙速度)：地球卫星的最小发射速度，在地面附近，卫星绕地球做圆周运动，万有引力提供向心力，而万有引力近似等于重力，所以有mg＝m，即环绕速度v₁＝(R为地球半径，g是地面附近的重力加速度)．

此式仅适用于紧靠地面的圆轨道上运行的卫星，将g、R值代入可得v₁＝7.9 km/s，即发射速度为7.9 km/s时卫星刚好紧靠地面的圆轨道运行．

3．第二宇宙速度：使物体可以挣脱地球引力的束缚，成为绕太阳运行的人造卫星(或飞到其他行星上去)的最小发射速度，其大小为11.2 km/s.

4．第三宇宙速度：使物体挣脱太阳引力的束缚，飞到太阳系以外的宇宙空间去的最小发射速度，其大小为16.7 km/s.

5．轨道运行速度：人造卫星在高空沿着圆轨道或椭圆轨道运行．若沿圆轨道运行，此时F_向＝F_引，即m＝G，所以v＝ .式中M为地球质量，r为卫星与地心之间的距离，v就是卫星绕地球运行的速率．此式适用于所有在绕地球圆轨道上运行的行星，由于v∝，所以v随r的增大而减小，即卫星离地球越远，其轨道速率就越小．当r＝R地时，v＝v1，即第一宇宙速度是轨道速度的特例；当r>R地时，v<v1.因此轨道速度总小于第一宇宙速度．换句话说，卫星绕地球运行的最大速度是7.9 km/s.

知识点二、卫星的运动规律及变轨问题

1.人造卫星的向心加速度、线速度、角速度、周期与半径的关系

卫星绕地球做匀速圆周运动时符合越高越慢的规律，根据G＝ma＝＝mω²r＝m²r，知a∝，v∝，ω∝，T∝.

2．卫星的变轨问题

卫星的变轨问题应结合离心运动和向心运动去分析，因为变轨的过程中不满足稳定运行的条件F万＝F向，而是在原轨道上因为速度减小做向心运动而下降，速度增大做离心运动而升高，但是一旦变轨成功后又要稳定运行，这时又满足F万＝F向．

知识点三、赤道上的物体与同步卫星以及近地卫星的运动规律 

1．地球赤道上的物体，静止在地面上与地球相对静止，随地球的自转绕地轴做匀速圆周运动．地球赤道上的物体所受地球的万有引力，其中的一个分力提供物体随地球自转做圆周运动的向心力，产生向心加速度a，另一个分力为重力，有G－mg＝ma(其中R为地球半径)．

2．近地卫星的轨道高度约等于地球半径，其所受万有引力完全提供卫星的向心力，即G＝ma.

3．同步卫星与赤道物体具有与地球自转相同的运转周期和运转角速度，始终与地球保持相对静止状态，共同绕地轴做匀速圆周运动．

知识点四、万有引力和重力的关系

宇宙间的一切物体都是相互吸引的，这种相互作用力叫做万有引力．地面上及地面附近的物体由于地球的吸引而受到的力叫做重力．

万有引力和重力的关系：实际上，地面上物体所受的万有引力F可以分解为物体所受的重力mg和随地球自转而做圆周运动的向心力F′.其中F＝G，F′＝mω²r.

(1)当物体在赤道上时，F、mg、F′三力同向．此时满足F′＋mg＝F.

(2)当物体在两极点时，F′＝0，F＝mg＝G.

(3)当物体在地球的其他位置时，三力方向不同，F＞mg.

(4)当忽略地球自转时，重力等于万有引力，即mg＝.

(5)对于绕地球运行的近地卫星，所受的万有引力就是卫星的重力．

知识点五、人造地球卫星的运动问题

1．人造卫星的运行规律

(1)由G＝得v＝ ，即v∝ ，轨道半径越大，环绕速度越小．

(2)由G＝mω²r得ω＝ ，即ω∝ .

(3)由G＝mr，得T＝2π ，即T∝，轨道半径越大，周期越大．

总结：近地卫星的线速度最大，周期最小．

2．两类运动——稳定运行和变轨运行

卫星绕天体稳定运行时，万有引力提供了卫星做圆周运动的向心力，即＝m，当卫星由于某种原因，其速度v突然变化时，F_万和m不再相等，因此就不能再根据v＝ 来确定r的大小．当F_万＞m时，卫星做近心运动；当F_万＜m时，卫星做离心运动．

知识点六、超重和失重现象

1．人造卫星的超重与失重

(1)人造卫星在发射升空时，有一段加速运动；在返回地面时，有一段减速运动，这两个过程加速度方向均向上，因而都是超重状态．

(2)人造卫星在沿圆轨道运行时，由于万有引力提供向心力，所以处于完全失重状态，在这种情况下凡是与重力有关的力学现象都会停止发生，因此，在卫星上的仪器，凡是制造原理与重力有关的均不能使用．同理，与重力有关的实验也将无法进行．

2．赤道上物体的失重问题

地球在不停地自转，除两极之外，地球上的物体由于绕地轴旋转，都处于失重状态，且赤道上的物体失重最多．

设地球是半径为R的均匀球体，自转角速度为ω，表面的重力加速度为g，质量为m的物体放在赤道上，地面对物体的支持力为FN，根据牛顿第二定律有mg－FN＝mω²R，则有

(1)物体在赤道上的视重等于地球的引力与物体随地球自转所需的向心力之差，即FN＝mg－mω²R；

(2)物体在赤道上的失重等于物体绕地轴转动所需要的向心力，即F＝mg－FN＝mω²R；

(3)物体在地球上完全失重的临界状态是物体受到的重力(或万有引力)完全提供随地球自转所需要的向心力，即FN＝0.

所以mg＝mω²R.在此条件下，可以求出对应的临界角速度、临界线速度、临界周期等物理量．

知识点七、与天体有关的估算问题

天体的估算问题一般涉及天体质量、密度、转动周期、线速度、转动半径等．天体的运动可以看成圆周运动，处理这类问题的基本思路有两条：

(1)利用天体做圆周运动的向心力由万有引力提供，天体的运动遵循牛顿第二定律求解．

即G＝ma

(2)利用天体表面的物体的重力约等于万有引力来求解

即G＝mgM＝ρ＝.

典例分析

一、万有引力公式的应用

例1 设地球半径为R，地球自转周期为T，地球同步卫星距赤道地面的高度为h，质量为m，试求此卫星处在同步轨道上运行时与处在赤道地面上静止时的：

(1)线速度之比．

(2)向心加速度之比．

(3)所需向心力之比．

解析　由于卫星在同步轨道上运行时与处在赤道地面上静止时，具有相同的运转角速度，故

(1)二者的线速度之比＝＝.

(2)二者的向心加速度之比＝＝.

(3)二者所需向心力之比＝＝.

答案　(1)　(2)　(3)

二、行星相遇问题

例2  如图所示有A、B两个行星绕同一恒星O做圆周运动，运转方向相同，A行星的周期为T₁，B行星的周期为T₂.在某一时刻两行星第一次相遇(即两行星相距最近)，则(　　)

A．经过时间t＝T₁＋T₂，两行星将第二次相遇

B．经过时间t＝，两行星将第二次相遇

C．经过时间t＝，两行星第一次相距最远

D．经过时间t＝，两行星第一次相距最远

解析 本题的难点在于A、B运动关系的建立，实质上属于“追及”问题，不过是圆周运动的追及相遇．在追及问题和相对运动问题中，巧选参考系往往使问题化繁为简，化难为易．

先根据开普勒定律判断哪个行星周期大，在此基础上通过空间想象和运动学知识列出相距最近、最远的运动学关系，便可求解．

据开普勒定律＝k可知T₂＞T₁.以B和行星中心连线为参考系，则A相对此参考系以ω₁－ω₂为相对角速度做匀速圆周运动，到第二次相遇即A相对参考系转过2π角度，这中间经历的时间t＝＝＝而从第一次相遇到第一次相距最远需相对参考系转过π角度，所以经过时间t′＝＝＝，选项B、D正确．

答案 BD

三、天体质量的估算

例3  已知引力常量G，地球半径R，月球和地球之间的距离r，同步卫星距地面的高度h，月球绕地球的运转周期T₁，地球的自转周期T₂，地球表面的重力加速度g.试根据以上条件，提出一种估算地球质量M的方法．

解析　解法一　同步卫星绕地球做匀速圆周运动，两者之间的万有引力提供卫星运动的向心力，由牛顿第二定律可得G＝ma＝m()²(R＋h)，解得M＝

解法二　以月球为研究对象，月球绕地球做圆周运动，万有引力提供向心力则G＝m()²r，解得M＝

解法三　在地球表面物体的重力近似等于万有引力，即G＝mg，所以M＝.

答案　见解析

四、关于卫星的发射问题

例4  一颗人造地球卫星以初速度v发射后，可绕地球做匀速圆周运动，若使发射速度增为2v ，则该卫星可能(　　)

A．绕地球做匀速圆周运动

B．绕地球运动，轨道变为椭圆

C．不绕地球运动，成为太阳系的人造行星

D．挣脱太阳引力的束缚，飞到太阳系以外的宇宙去了

解析　以初速度v发射后能成为人造地球卫星，可知发射速度v一定大于第一宇宙速度7.9 km/s；当以2v速度发射时，发射速度一定大于15.8 km/s，已超过了第二宇宙速度11.2 km/s，所以此卫星不再绕地球运行，可能绕太阳运行，或者飞到太阳系以外的空间去了，故选项C、D正确．

答案　CD

归纳总结：发射速度是指卫星在地面附近离开发射装置时的初速度，要发射一颗人造地球卫星，发射速度不能小于第一宇宙速度，即最小发射速度是7.9 km/s；若要发射一颗轨道半径大于地球半径的人造人星，发射速度必须大于7.9 km/s.可见，向高轨道发射卫星比向低轨道发射卫星要困难．

运行速度是指卫星在进入运行轨道后绕地球运行时的线速度．当卫星“贴着”地面(即近地)飞行时，运行速度等于第一宇宙速度，当卫星的轨道半径大于地球半径时，运行速度小于第一宇宙速度，所以最大运行速度是7.9 km/s.

五、双星问题

例5  宇宙中两个相距较近的天体称为“双星”，它们以两者连线上的某一点为圆心做匀速圆周运动，但两者不会因万有引力的作用而吸引到一起．设两者的质量分别为m₁和m₂，两者相距为L.求：

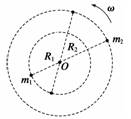
(1)双星的轨道半径之比．

(2)双星的线速度之比．

(3)双星的角速度．

解析　这两颗星必须各自以一定的速度绕某一中心转动才不至于因万有引力作用而吸引在一起，从而保持两星间距离L不变，且两者做匀速圆周运动的角速度ω必须相同．如图所示，两者轨迹圆的圆心为O，圆半径分别为R₁和R₂.由万有引力提供向心力，有

G＝m₁ω²R₁①

G＝m₂ω²R₂②

(1)由①②两式相除，得＝.

(2)因为v＝ωR，所以＝＝.

(3)由几何关系知R₁＋R₂＝L③

联立①②③式解得ω＝ .

答案　(1)m₂∶m₁　(2)m₂∶m₁　(3)

归纳总结：所谓“双星”问题，是指在宇宙中有两个相距较近的天体，它们靠相互吸引力提供向心力做匀速圆周运动，两者有共同的圆心，且间距不变，则向心力大小也不变，其他天体距它们很远，对其影响忽略不计．双星的连线一定过圆轨道的圆心，它们之间的万有引力提供向心力，其特点为：双星的周期一定相同，角速度也相同，半径之和为两星间距.