第七章  万有引力与宇宙航行

第1节　行星的运动

知识点归纳

知识点一、开普勒行星运动定律

定律	内容	图示或公式
开普勒第一定律(又称轨道定律)	所有行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上
开普勒第二定律(又称面积定律)	对任意一个行星来说，它与太阳的连线在相等的时间内扫过相等的面积
开普勒第三定律(又称周期定律)	所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等 公式：＝k，k是一个与行星无关的常量

知识点二、开普勒行星运动定律的实际应用

1．行星绕太阳运动的轨道十分接近圆，太阳处在圆心．

2．对某一行星来说，它绕太阳转动的角速度(或线速度太小) 不变，即行星做匀速圆周运动．

3．所有行星轨道半径的三次方跟它的公转周期的二次方比值都相等．

知识点三、对开普勒行星运动定律的理解

开普勒行星运动定律是根据行星运动的观测结果总结归纳出来的规律，它的每一条都是经验定律，都是从观测行星运动所取得的资料中总结出来的，开普勒行星运动定律只涉及运动学、几何学方面的内容．

1．开普勒第一定律说明了不同行星绕太阳运动时的椭圆轨道是不同的，在行星的轨道上出现了近日点和远日点．

2．开普勒第二定律说明行星在近日点的速率大于在远日点的速率，从近日点向远日点运动时速率变小，从远日点向近日点运动时速率变大．

3．开普勒第三定律的表达式为＝k，它反映了行星的公转周期跟轨道半长轴之间的依存关系．椭圆轨道半长轴越长的行星，其公转周期越大；反之，其公转周期越小．

4．k是由中心天体决定的，中心天体不同则k值不同．例如：地球围绕太阳运动，k是由中心天体太阳决定的；月球围绕地球运动，k是由中心天体地球决定的，而这两个常量是不同的．

典例分析

一、开普勒三定律的理解

例1 关于行星的运动，下列说法正确的是            (　　)．

A．行星轨道的半长轴越长，自转周期就越大

B．行星轨道的半长轴越长，公转周期就越大

C．水星轨道的半长轴最短，公转周期最小

D．海王星离太阳“最远”，绕太阳运行的公转周期最大

解析　由开普勒第三定律可知，＝k(常量)．则行星轨道的半长轴越长，公转周期越大，选项B正确．水星轨道的半长轴最短，其公转周期最小，选项C正确．海王星离太阳“最远”，绕太阳运行的公转周期最大，选项D正确．公转轨道半长轴的大小与自转周期无关，选项A错误．

答案　BCD

二、开普勒第二定律的应用

例2  一颗人造地球卫星绕地球做椭圆运动，地球位于椭圆轨道的一个焦点上，如图所示，地球距离卫星的近地点A的距离为L，距离卫星的远地点B的距离为s，求卫星在A点和B点的速度之比．

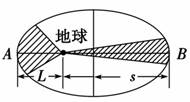
解析：设卫星在A点时的速度为vA，在B点时的速度为vB．在A点附近截取一小段曲线，则此段曲线可看成是一小段圆弧，半径为L，弧长为l1；同理，在B点附近也截取一小段曲线看成是以地球为圆心的一小段圆弧，半径为s，弧长为l2．分别将圆弧两端与地心相连，如图所示．设在A点运动弧长l1和在B点运动弧长l2用时相等．

即＝．

由于在A点附近速度大小变化很小，所以有l₁＝v_At；同理，在B点附近，l₂＝v_Bt．

所以＝，lv_A＝sv_B，即v_A：v_B＝s：L．

答案：s：L

归纳总结：1．开普勒第二定律不仅适用于以太阳为中心天体的运动，而且也适用于以地球或其他星体为中心天体的运动．

2．由开普勒第二定律可知：行星从近日点向远日点运动，其速率减小，而由远日点向近日点运动，其速率增大．

3．在很短一段时间内，可以认为行星在近日点和远日点都做圆周运动，根据弧长公式l＝Rθ和扇形面积公式S＝lR知，S＝R²θ．

三、开普勒第三定律的应用

例3  继美国发射的可重复使用的运载火箭后，印度称正在设计可重复使用的宇宙飞船，预计将在2030年发射成功，这项技术将使印度在太空领域占有优势．假设某飞船沿半径为R的圆周绕地球运行，其圆周期为T，地球半径为R0．该飞船要返回地面时，可在轨道上某点A处将速率降到适当数值，从而沿着以地心为焦点的椭圆轨道运动，椭圆与地球表面的B点相切，如图所示．求该飞船由A点运动到B点所需的时间．

解析　飞船沿半径为R的圆周绕地球运动时，可认为其半长轴a＝R

飞船返回地面时，沿以地心为焦点的椭圆轨道运行，飞船由A点运动到B点的时间为其沿椭圆轨道运动周期T′的一半．

椭圆轨道的半长轴a′＝(R＋R₀)，

由开普勒第三定律得＝

所以t＝T′＝T．

答案　T

归纳总结：解该类问题需注意以下两点：(1)对于行星或卫星，只要是围绕同一中心天体运行的天体，＝k都成立．

(2)注意找出天体运行中的隐含条件，如地球公转周期为1年，自转周期为1天，月球公转周期为1个月．

自我检测

1．关于行星运动，下列说法正确的是(　　)

A．地球是宇宙的中心，太阳、月亮及其他行星都绕地球运动

B．太阳是宇宙的中心，地球是围绕太阳的一颗行星

C．宇宙每时每刻都是运动的，静止是相对的

D．不论是日心说还是地心说，在研究行星运动时都是有局限的

解析　宇宙是一个无限的空间，太阳系只是其中很小的一个星系，日心说的核心是认为太阳是行星运动的中心，故选C、D正确．

答案　CD

2．16世纪，哥白尼根据天文观测的大量资料，经过40多年的天文观测和潜心研究，提出了“日心说”的如下四个基本论点，这四个论点目前看存在缺陷的是(　　)

A．宇宙的中心是太阳，所有行星都在绕太阳做匀速圆周运动

B．地球是绕太阳做匀速圆周运动的行星，月球是绕地球做匀速圆周运动的卫星，它绕地球运动的同时还跟地球一起绕太阳运动

C．天穹不转动，因为地球每天自西向东自转一周，造成天体每天东升西落的现象

D．与日地距离相比，其他恒星离地球都十分遥远，比日地间距离大得多

解析　天文学家开普勒在认真整理了第谷的观测资料后，在哥白尼学说的基础上，抛弃了圆轨道的说法，提出了以大量观测资料为依据的开普勒三定律，揭示了天体运动的真相，所有行星围绕太阳运动的轨道为椭圆，太阳处于所有椭圆的一个焦点上，整个宇宙是在不停运动的．故A、B、C选项的说法存在缺陷．

答案　ABC

3．关于开普勒行星运动的公式＝k，下列理解正确的是(　　)

A．k是一个与行星无关的量

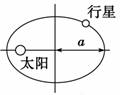
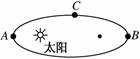
B．若地球绕太阳运转轨道的半长轴为a_地，周期为T_地；月球绕地球运转轨道的半长轴为a_月，周期为T_月，则＝

C．T表示行星运动的自转周期

D．T表示行星运动的公转周期

解析　＝k是指围绕太阳的行星或者指围绕某一行星的卫星半长轴与周期的关系，T是公转周期，k是一个与环绕星体无关的量，只与被环绕的中心天体有关，中心天体不同，其值不同，只有围绕同一天体运动的行星或卫星，它们半长轴的三次方与公转周期的二次方之比才是同一常数．故≠．

答案　AD

4．某行星绕太阳运动的椭圆轨道如图所示，则下列说法中正确的是(　　)

   

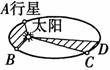
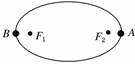
A．该行星在A点速度最大，在B点速度最小

B．该行星在A点速度最大，在C点速度最小

C．该行星在B点速度最大，在A点速度最小

D．该行星在C点速度最大，在B点速度最小

解析　由开普勒第二定律可知，行星在近日点速度最大，在远日点速度最小，故A选项正确．

答案　A

5．哈雷彗星绕太阳运动的轨道是比较扁的椭圆，下列说法中不正确的是(　　)

A．彗星在近日点的速率大于在远日点的速率

B．彗星在近日点的角速度大于在远日点的角速度

C．彗星在近日点的向心加速度大于在远日点的向心加速度

D．若彗星周期为75年，则它的半长轴是地球公转半径的75倍

解析　根据开普勒第二定律，为使相等时间内扫过的面积相等，则应保证在近日点与远日点相比在相同时间内走过的弧长要大．因此在近日点慧星的线速度(即速率)、角速度都较大，故A、B正确．而向心加速度a＝，在近日点，v大、R小，因此a大，故C正确．根据开普勒第三定律＝k，则＝＝75²，即a₁＝a₂，D错误．

答案　D

6．关于行星绕太阳运动的下列说法中正确的是(　　)

A．所有行星都在同一椭圆轨道上绕太阳运动

B．行星绕太阳运动时太阳位于行星轨道的中心处

C．离太阳越近的行星的运动周期越长

D．所有行星的轨道半长轴的三次方跟公转周期的二次方的比值都相等

解析　所有的行星绕太阳运动的轨道都是椭圆，但不是同一轨道，太阳处在椭圆的一个焦点上，故A、B错；所有行星的轨道半长轴的三次方跟公转周期的二次方的比值都相等，离太阳越近的行星，其运动周期越短，故C项错，D项对．

答案　D

7．已知两个行星的质量m₁＝2m₂，公转周期T₁＝2T₂，则它们绕太阳运转轨道的半长轴之比为(　　)

A．＝  B．＝  C．＝  D．＝

解析　由开普勒第三定律＝k，分析得C项正确．

答案　C

8．某行星绕太阳运动的椭圆轨道如图所示，F₁和F₂是椭圆轨道的两个焦点，行星在A点的速率比在B点的速率大，则太阳位于(　　)

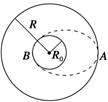
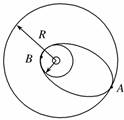
A．F₂                                                           B．A

C．F₁                                                           D．B

解析　根据开普勒第二定律，行星和太阳的连线在相等的时间内扫过相等的面积，故行星在近日点的运行速率大于在远日点的速率，由题意可知行星在A点的速率大于在B点的速率，所以太阳位于F₂位置，故选项A正确．

答案　A

9．假设行星绕太阳运动的轨道是圆形，火星与太阳的距离比地球与太阳的距离大53%，试确定火星上一年是多少地球年？

解析　设地球距太阳距离为R

则火星距太阳为R_火＝R＋0.53 R＝1.53 R

由开普勒第三定律＝k，得＝，代入已知量得T_火＝1.9T_地．

答案　1.9

10．两个质量分别是m₁、m₂的人造地球卫星，分别绕地球做匀速圆周运动，若它们的轨道半径分别是R₁和R₂，则它们的运行周期之比是多少？

解析　所有人造卫星在绕地球运转时，都遵守开普勒第三定律．因此，对这两个卫星有＝，所以它们的运行周期之比＝ ＝()．

答案　

11．如图所示，飞船沿半径为R的圆周绕地球运动，其周期为T，地球半径为R₀，若飞船要返回地面，可在轨道上某点A处将速率降到适当的数值，从而使飞船沿着以地心为焦点的椭圆轨道运行，椭圆与地球表面在B点相切，求飞船由A点到B点所需要的时间．

解析　当飞船做半径为R的圆周运动时，由开普勒第三定律＝k，

当飞船返回地面时，从A处降速后沿椭圆轨道至B，设飞船沿椭圆轨道运动的周期为T′，椭圆的半长轴为a，则＝k可解得T′＝ ·T

由于a＝，由A到B的时间为t＝

可知t＝＝ ·T＝·

答案　·