|
第六章 章末总结 要点归纳知识点一、圆周运动的运动学分析 (1)正确理解描述圆周运动快慢的物理量及其相互关系 线速度、角速度、周期和转速都是描述圆周运动快慢的物理量,但意义不同.线速度描述物体沿圆周运动的快慢.角速度、周期和转速描述做圆周运动的物体绕圆心转动的快慢.由ω==2πn,知ω越大,T越小,n越大,则物体转动得越快,反之则越慢.三个物理量知道其中一个,另外两个也就成为已知量. (2)对公式v=ωr及a==ω2r的理解 ①由v=ωr,知r一定时,v与ω成正比;ω一定时,v与r成正比;v一定时,ω与r成反比. ②由a==ω2r,知v一定时,a与r成反比;ω一定时,a与r成正比. 知识点二、圆周运动的动力学分析 匀速圆周运动是一种变加速曲线运动,处理匀速圆周运动问题不能应用运动的合成与分解方法,而应抓住合力充当向心力这一特点,由牛顿第二定律来分析解决,此时公式F=ma中的F是指向心力,a是指向心加速度,即ω2r或或其他的用转速、周期、频率表示的形式. 知识点三、圆周运动中临界问题的分析 (1)当物体从某种特性变化为另一种特性时,发生质的飞跃的转折状态,通常叫做临界状态.出现临界状态时,即可理解为“恰好出现”,也可理解为“恰好不出现”. (2)确定临界状态的常用方法 ①极限法:把物理问题(或过程)推向极端,从而使临界现象显现,达到尽快求解的目的. ②假设法:有些物理过程中没有明显出现临界问题的线索,但在变化过程中可能出现临界问题. (3)水平面内的圆周运动临界问题 关于水平面内匀速圆周运动的临界问题,要特别注意分析物体做圆周运动的向心力来源,考虑达到临界条件时物体所处的状态,即临界速度、临界角速度,然后分析该状态下物体的受力特点,结合圆周运动知识,列方程求解. 典例分析 一、圆锥中的圆周运动
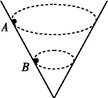
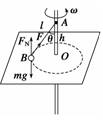
A.球A的线速度必定大于球B的线速度 B.球A的角速度必定大于球B的角速度 C.球A的运动周期必定小于球B的运动周期 D.球A对筒壁的压力必定大于球B对筒壁的压力 解析 由于A,B质量相同,在相同的倾斜面上,则向心力相等,进一步可知两球所受的弹力相等,故选项D错误;根据F向=ma可知,A,B两小球实际上是具有相同的向心加速度,根据a= 答案 A 二、转盘的圆周运动
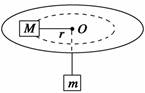
解析 当ω取较小值ω1时,M有向O点滑动趋势,此时M所受静摩擦力背离圆心O,对M有:mg-Fmax=Mωr,代入数据得:ω1=1 rad/s. 当ω取较大值ω2时,M有背离O点滑动趋势,此时M所受静摩擦力指向圆心O,对M有:mg+Fmax=Mωr代入数据得:ω2=3 rad/s 所以角速度的取值范围是:1 rad/s≤ω≤3 rad/s. 答案 1 rad/s≤ω≤3 rad/s 三、竖直平面内的圆周运动
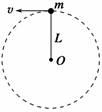
(1)当小球在最高点的速度为多大时,球对杆的作用力为零? (2)当小球在最高点的速度分别为6 m/s和1.5 m/s时,球对杆的作用力的大小与方向. 解析 (1)此时mg=,v==3 m/s (2)设最高点杆对球作用力为F,方向向下,则F+mg=,分别代入v1=6 m/s和v2=1.5 m/s,得F1=6 N、F2=-1.5 N,由牛顿第三定律,球对杆的作用力F1′=6 N方向向上,F2′ 答案 (1)3 m/s (2)6 N 方向向上 1.5 N 方向向下 归纳总结:对于物体在竖直平面内做变速圆周运动的问题,中学物理中只研究物体通过最高点和最低点的情况,并且经常出现临界状态.通常有以下两种情况: ①没有物体支撑的小球(轻绳或单侧轨道类) 小球在最高点的临界速度(最小速度)是v0=.小球恰能通过圆周最高点时,绳对小球的拉力为0,环对小球的弹力为0(临界条件:FT=0或FN=0),此时重力提供向心力.所以v≥时,能通过最高点;v<时,不能达到最高点. ②有物体支撑的小球(轻杆或双侧轨道类) 因轻杆和管壁能对小球产生支撑作用,所以小球达到最高点的速度可以为0,即临界速度v0=0,此时支持力FN=mg. 四、圆周运动的临界问题
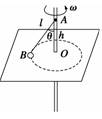
A. B.π C. D.2π 解析 如图所示,以小球为研究对象,小球受三个力的作用,重力mg、水平面支持力FN、绳子拉力F.在竖直方向合力为零,在水平方向所需向心力为,而R=htan θ,得 Fcos θ+FN=mg Fsin θ==mω2R=m4π2n2R=m4π2n2htan θ
当球即将离开水平面时,FN=0,转速n有最大值. FN=mg-m4π2n2h=0 n= ,故选A. 答案 A 归纳总结:1.分析圆周运动的思路,即动力学思路,关键是受力分析,明确F向来源,应用F向=m等公式求解. 2.分析临界问题一般是令某量达到极值,寻找临界条件,以临界条件作为突破口. 五、圆周运动与平抛运动的结合
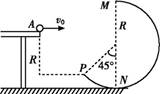
(1)小球在A点的初速度v0及AP间水平距离x; (2)小球到达圆轨道最低点N时对N点的压力; (3)判断小球能否到达圆轨道最高点M。 解析 (1)小球由A点做平抛运动,在P点恰好沿圆轨道的切线进入轨道,则小球在P点的竖直分速度为vy=v0tan 45°=v0 由平抛运动规律得vy=gt,R= 解得v0=4 m/s,x=1.6 m。 (2)小球在P点的速度为v= 小球从P点到N点,由动能定理得mgR(1-cos 45°)= 小球在N点,由牛顿第二定律得FN-mg=m 解得小球所受支持力FN=11.17 N 由牛顿第三定律得,小球对N点的压力为FN′=11.17 N,方向竖直向下。 (3)假设小球能够到达M点,对小球由P点到M点由动能定理得 mgR(1+cos 45°)= 解得v′= 小球能够完成圆周运动,在M点应有mg≤ 由v′<vM知,小球不能到达圆轨道最高点M。 答案 (1)4 m/s 1.6 m (2)11.17 N 方向竖直向下 (3)见解析 |