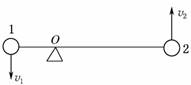第六章　圆周运动

第1节　圆周运动

知识点归纳

知识点一、线速度

1．定义：物体做圆周运动通过的弧长与通过这段弧长所用时间的比值。

2．定义式： v=。Δs是在时间Δt内通过的弧长，线速度的单位是m/s．

3．标、矢性：线速度是矢量，方向与圆弧相切，与半径垂直。

4．匀速圆周运动：

(1)定义：沿着圆周，并且线速度的大小处处相等的运动。

(2)性质：线速度的方向是时刻变化的，所以是一种变速运动。

知识点二、角速度

1．定义：连接物体与圆心的半径转过的角度与转过这一角度所用时间的比值。

2．定义式： ω=。

3．单位：弧度每秒，符号是rad/s或rad·s-1。

4．匀速圆周运动的角速度：匀速圆周运动是角速度不变的圆周运动。

5．转速与周期：

6． 频率、周期和转速三者关系：f＝，f＝n(n的单位取r/s)

知识点二、线速度与角速度的关系

1．两者关系:在圆周运动中,线速度的大小等于角速度大小与半径的乘积。

2．关系式:v=ωr。

知识点三、线速度和角速度的比较

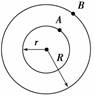
知识点四、v、ω、r中有一个不变时，其他两个变量的变化关系：

1．对角速度、周期、转速之间关系的理解：物体做匀速圆周运动时，由ω＝＝2πn知，角速度、周期、转速三个物理量，只要其中一个物理量确定了，其余两个物理量也唯一确定了．

2．对线速度与角速度关系的理解：由v＝ωr知，r一定时，v∝ω；v一定时，ω∝；ω一定时，v∝r．

知识点四、传动问题中v、ω、T与r的关系

1．同轴传动．

如图所示，A点和B点在同轴的一个“圆盘”上，所以角速度相同．但因A、B两点与轴的距离不同，即转动半径不同，所以线速度不同，设半径分别为r和R，且r<R，其线速度、角速度、周期之间存在的定量关系为：，ωA＝ωB，TA＝TB．

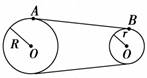
2．皮带传动．

如图所示，A点和B点分别是两个轮子边缘上的点，两个轮子用皮带连起来，并且皮带不打滑，所以它们的线速度必然相同，但是因为半径不同，所以角速度不同．线速度、角速度、周期之间存在的定量关系为：vA＝vB，＝，＝．

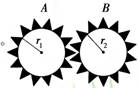
3．齿轮传动．

如图所示，A点和B点分别是两个齿轮边缘上的点，两个齿轮轮齿啮合．两个轮子在同一时间内转过的齿数相等，或者说A、

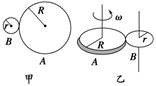
B两点的线速度相等，但它们的转动方向恰好相反，即当A

顺时针转动时，B逆时针转动．线速度、角速度、周期之间存在的定量关系为：vA＝vB，＝＝，＝＝，式中n1、n2分别表示齿轮的齿数．

4．摩擦传动

         如图所示，两摩擦轮靠摩擦进行传动，A点和B点分别是两轮边缘上的点，传动时如果两摩擦轮在接触处没有相对滑动，则两轮在接触处的线速度大小相等，此时A点和B点的线速度、角速度、周期存在以下定量关系： v_A＝v_B，＝，＝．

典例分析

一、描述圆周运动的物理量的理解

例1  关于做匀速圆周运动物体的线速度、角速度、周期之间的关系，下列说法正确的是(　　)

A．线速度大的角速度一定大

B．线速度大的周期一定小

C．角速度大的半径一定小

D．角速度大的周期一定小

解析　由v＝ωr得ω＝，故只有当半径r一定时，角速度ω才与线速度v成正比；只有当线速度v一定时，角速度ω才与半径r成反比，A、C错．由v＝知只有当半径r一定时，线速度v才与周期T成反比，B错．由ω＝知角速度ω与周期T成反比，即角速度大的周期一定小，D正确．

答案　D

归纳总结：公式v＝ωr，在半径不确定的情况下，不能由角速度大小判断线速度大小，也不能由线速度大小判断角速度的大小，但由ω＝可看出，角速度越大，周期越小．

二、传动装置中各物理量间的关系问题

例2 如图所示的传动装置中，B、C两轮固定在一起绕同一转轴转动，A、B两轮用皮带转动，三轮半径关系是r_A＝r_C＝2r_B．若皮带不打滑，求A、B、C轮边缘的a、b、c三质点的角速度之比和线速度之比．

解析　A、B两轮通过皮带转动，且皮带不打滑，则A、B两轮边缘的线速度大小相等，即v_a＝v_b或v_a∶v_b＝1∶1①

由v＝ωr得ω_a∶ω_b＝r_B∶r_A＝1∶2②

B、C两轮固定在一起绕同一轴转动．则B、C两轮的角速度相同，即

ω_b＝ω_c或ω_b∶ω_c＝1∶1③

由v＝ωr得v_b∶v_c＝r_B∶r_C＝1∶2④

由②③得ω_a∶ω_b∶ω_c＝1∶2∶2

由①④得v_a∶v_b∶v_c＝1∶1∶2

答案　1∶2∶2　1∶1∶2

归纳总结：(1)皮带传动(线速度大小相等)．

(2)同轴传动(角速度相等)．

(3)齿轮传动(线速度大小相等)．

(4)摩擦传动(线速度大小相等)．

三、与圆周运动结合的综合问题

例3  如图所示，直径为d的纸制圆筒以角速度ω绕垂直纸面的轴O匀速转动(图示为截面)．从枪口发射的子弹沿直径穿过圆筒，若子弹在圆筒旋转不到半周时，在圆周上先后留下a、b两个弹孔，已知aO与bO夹角为θ，求子弹的速度．

解析　通过圆周运动转过的角度求出运动的时间，该运动时间也是直线运动的时间，再根据直线运动的位移，即可求出直线运动的速度．子弹射出后沿直线运动，从a点射入，从b点射出，该过程中圆筒转过的角度为π－θ．

设子弹速度为v，则子弹穿过圆筒的时间t＝．

此时间内圆筒转过的角度α＝π－θ，据α＝ωt得π－θ＝ω，则子弹速度v＝．

答案　

归纳总结：解决此类问题关键要抓住物体做直线运动的时间与圆周运动的时间相等，若无角度的限制，转过的角度应加上2π·n(n＝1、2、3、…)，注意题目给出的条件．

自我检测

1．做匀速圆周运动的物体，下列各物理量中不变的是(　　)

A．线速度                                                    B．角速度

C．周期                                                        D．转速

解析　圆周运动的物体线速度是矢量，其方向时刻变化，故A选项错误；匀速圆周运动的角速度大小和方向都不变，周期和转速是标量，匀速圆周运动其值不变，故B、C、D选项正确．

答案　BCD

2．下列关于甲、乙两个做匀速圆周运动的物体的有关说法正确的是(　　)

A．甲、乙两物体线速度相等，角速度一定也相等

B．甲、乙两物体角速度相等，线速度一定也相等

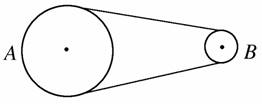
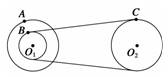
C．甲、乙两物体周期相等，角速度一定也相等

D．甲、乙两物体周期相等，线速度一定也相等

解析　由ω＝可知，周期相同，角速度一定也相等，故C选项正确．

答案　C

3．如下图所示，两个皮带轮通过皮带传动(皮带与轮不发生相对滑动)．大轮半径是小轮半径的2倍，设A、B分别是大小轮轮缘上的一点，现比较它们的线速度v、角速度ω、周期T和频率f之间的关系，正确的是(　　)

①v_A：v_B＝1：2  ②ω_A：ω_B＝1：2   ③T_A：T_B＝1：2  ④f_A：f_B＝1：2

A．①②       B．②③        C．②④        D．①④

解析　A、B分别是大、小轮轮缘上的点，由题意可知，v_A＝v_B，v_A＝ω_Ar_A，v_B＝ω_Br_B，所以ω_A：ω_B＝1：2，f_A：f_B＝1：2．

答案　C

4．关于匀速圆周运动的角速度和线速度，下列说法正确的是(　　)

A．半径一定，角速度与线速度成反比

B．半径一定，角速度与线速度成正比

C．线速度一定，角速度与半径成正比

D．角速度一定，线速度与半径成反比

解析　由v＝ω·r可知，r一定时，ω∝v，故A错，而B正确．v一定时，ω∝，故C错；ω一定时，v∝r，故D错．

答案　B

5．地球自转一周为一昼夜时间(24 h)，新疆乌鲁木齐市处于较高纬度地区，而广州则处于低纬度地区，由于地球自转方向由西向东，每天早晨广州要比乌鲁木齐天亮得早，关于两地所在处物体具有的角速度和线速度相比较(　　)

A．乌鲁木齐处物体的角速度大，广州处物体的线速度大

B．乌鲁木齐处物体的线速度大，广州处物体的角速度大

C．两处物体的角速度、线速度都一样大

D．两处物体的角速度一样大，但广州物体的线速度比乌鲁木齐处物体线速度要大

解析　由于地球绕地轴由西向东自转，地球上任何点都在随地球自转，具有相同的周期，根据ω＝可知，地球上不同区域的自转角速度相同，但由于纬度不同，不同区域的自转线速度大小不相等，纬度越低，自转的半径越大．由v＝ωr可知，广州的物体自转的线速度大于乌鲁木齐处物体的线速度，选项D正确．

答案　D

6．由“嫦娥奔月”到“万户飞天”，由“东方红”乐曲响彻寰宇到航天员杨利伟遨游太空，中华民族载人航天的梦想已变成现实．“神舟”五号飞船升空后，先运行在近地点高度200千米、远地点高度350千米的椭圆轨道上，实施变轨后，进入343千米的圆轨道．假设“神舟”五号实施变轨后做匀速圆周运动，共运行了n周，起始时刻为t₁，结束时刻为t₂，运行速度为v，半径为r．则计算其运行周期可用(　　)

A．T＝                B．T＝

C．T＝                  D．T＝

解析　由题意可知飞船做匀速圆周运动n周所需时间Δt＝t₂－t₁，故其周期T＝＝，故选项A正确．由周期公式有T＝，故选项C正确．

答案　AC

7．两个小球固定在一根长为L的杆的两端，绕杆上的O点做圆周运动，如下图所示．当小球1的速度为v₁时，小球2的速度为v₂，则转轴O到小球2的距离为(　　)

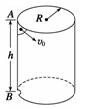
A．L     B．L         C．L         D．L

解析　两小球固定于同一杆的两端，绕同一轴转动，故角速度相同，因此，v₁＝ωR₁，v₂＝ωR₂，且R₁＋R₂＝L，联立解得R₂＝L．

答案　B

8．如图所示，竖直薄壁圆筒内壁光滑，其半径为R，上部侧面A处开有小口，在小口A的正下方h处亦开有与A大小相同的小口B，小球从小口A沿切线方向水平射入筒内，使小球紧贴筒内壁运动．要使小球从B口处飞出，小球进入A口的最小速率v₀为(　　)

  

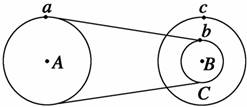
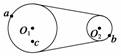
A．πR                 B．πR

C．πR                 D．2πR

解析　小球在竖直方向上做自由落体运动，则h＝gt²，又由于圆筒内壁光滑，故小球沿水平方向做匀速圆周运动．若小球恰能从B点飞出，则水平方向做圆周运动的最短路程s＝2πR，所以小球刚进入入口时的速度为v＝＝2πR ＝πR ，故B选项正确．

答案　B

9．一质点做圆周运动，在时间t内转过n周．已知圆周半径为R，则该质点的线速度大小为(　　)

A．                                                         B．

C．                                                          D．

解析　质点做圆周运动的周期T＝，由公式v＝得v＝＝，故B选项正确．

答案　B

10．如图所示为一皮带传送装置，a、b分别是两轮边缘上的两点，c处在O₁轮上，且有r_a＝2r_b＝2r_c，下列关系正确的有(　　)

 

A．v_a＝v_b    B．ω_a＝ω_b    C．v_a＝v_c     D．ω_a＝ω_c

解析　由皮带传动特点可知v_a＝v_b，所以A正确；再由v＝rω可知＝＝，B错误．由共轴传动特点可知，ω_a＝ω_c，D正确．再由v＝rω可知，＝＝，所以C错误．

答案　AD

11．一小球沿半径为2 m的轨道做匀速圆周运动，若周期T＝πs，则(　　)

A．小球的线速率是4 m/s

B．经过s，小球的位移为π m

C．经过s，小球的位移为2 m

D．经过s，小球的位移大小为4 m

解析　根据v＝得v＝m/s＝4 m/s故A选项正确；经过s即经周期，小球的位移为x＝r＝2 m，故C选项正确，B选项错误；同理经s小球经过半个圆周，其位移为2r＝4 m，故D选项正确．

答案　ACD

12．如图所示的传动装置中，A、B、C三个轮子的半径r_A＝r_C＝2r_B．A、B两轮共轴，在皮带不打滑时，三个轮子转动的角速度之比ω_A∶ω_B∶ω_C＝________；三个轮子边缘上各点的线速度之比v_A∶v_B∶v_C＝________；三个轮子边缘上各点的周期之比T_A∶T_B∶T_C＝________．

 

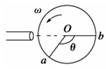
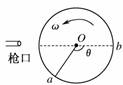
解析　因同一轮子上各点的角速度都相等，皮带传动(皮带

不打滑)中与皮带接触的轮缘上各点的线速度大小都相等(因各点在相等的时间内转过的圆弧长度相等)，故ω_A＝ω_B，B、C轮缘上点的线速度相等，即v_B＝v_C．由于v＝ωr．所以ω_B∶ω_C＝∶＝r_C∶r_B＝2∶1，故ω_A∶ω_B∶ω_C＝2∶2∶1；v_A∶v_B∶v_C＝ω_Ar_A∶ω_Br_B∶ω_Cr_C＝2∶1∶1；由于T＝，故T_A∶T_B∶T_C＝1∶1∶2．

答案　2∶2∶1　2∶1∶1　1∶1∶2

13．如图所示，直径为d的纸制圆筒以角速度ω绕垂直纸面的轴O匀速运动(图示为截面)．从枪口发射的子弹沿直径穿过圆筒．若子弹在圆筒旋转不到半周时，在圆周上留下a、b两个弹孔，已知aO与bO夹角为θ，求子弹的速度．

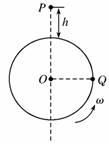
解析　设子弹速度为v，则子弹穿过筒的时间t＝．

此时间内圆筒转过的角度α＝π－θ．

据α＝ωt，得π－θ＝ω，

则子弹速度v＝ ．

答案　

14．如图所示，小球Q在竖直平面内做匀速圆周运动，半径为r，当Q球运动到与O在同一水平线上时，有另一小球P在圆面内距圆周最高点为h处开始自由下落，要使两球在圆周最高点处相碰，Q球的角速度ω应满足什么条件？

解析　由自由落体运动的位移公式h＝gt²，可求得小球P自由下落至圆周最高点的时间t₁＝ ．①

设小球Q做匀速圆周运动的周期为T，则有T＝，②

由题意知，小球Q由图示位置至圆周最高点所用的时间

t₂＝T(n＝0,1,2，…)．③

要使两球在圆周最高点相碰，需使t₁＝t₂，④

①②③④式联立，解得小球Q做匀速圆周运动的角速度

ω＝π(4n＋1) (n＝0,1,2，…)．

答案　见解析