|
|
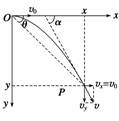
空中运动的总时间t |
t=,由高度 h决定,与初速度v0无关 |
|
离抛出点的最大高度h |
落地点竖直位移为h,与v0无关 |
|
水平位移x的大小 |
x=v0,与初速度及高度h都有关系 |
|
落地速度v的大小 |
v=,由水平初速度v0及高度h决定 |
|
速度方向、位移方向与水平面夹角 α和θ的关系 |
α、θ都随h(或t)的增大而增大,tan α=2 tan θ |
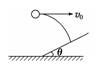
知识点三、斜抛运动的规律
斜抛运动可以看成是水平方向的匀速直线运动和竖直方向的竖直上抛或竖直下抛运动的合运动.如图所示,斜上抛物体初速度为v0,与水平方向间夹角为θ,则
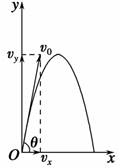
1.速度公式:水平速度vx=v0cos θ,竖直速度vy=v0sin θ-gt.
2.位移公式:水平位移x=v0cos θ·t,竖直位移y=v0sin θ·t-gt2.
3.轨迹方程:由水平位移公式和竖直位移公式可得:y=xtan θ-x2,这就是斜抛物体的轨迹方程.由上式可以看出:y=0时,x=0是抛出点位置,而x=是水平射程,并由此式可知,当θ=45°时,水平射程最大.
典例分析
一、抛体运动概念的理解
![]() 例1
例1![]() 做斜上抛运动的物体,到达最高点时( )
做斜上抛运动的物体,到达最高点时( )
A.具有水平方向的速度和水平方向的加速度
B.速度为0,加速度向下
C.速度不为0,加速度为0
D.具有水平方向的速度和向下的加速度
解析 斜上抛运动可以看成水平方向的匀速直线运动和竖直方向的竖直上抛运动的合运动.当物体到达最高点时,竖直方向上的速度减为0,水平方向上的速度不变.由于只受重力作用,所以物体始终具有竖直向下的加速度g,故D正确.
答案 D
归纳总结:判断物体是否做匀变速运动,只需看物体的加速度(或物体的合外力),只要是物体的加速度(或物体的合外力)恒定就是匀变速运动.加速度恒定指大小和方向都不变,而匀变速运动又因加速度(或合外力)与速度有共线和不共线两种,所以匀变速运动包括匀变速直线运动和匀变速曲线运动.
二、平抛运动规律的应用
![]() 例2
例2![]() 玉树大地震,牵动了全国人民的心.一架装载救灾物资的直升飞机,以10 m/s的速度水平飞行,在距地面180 m的高度处,欲将救灾物资准确投放至地面目标,若不计空气阻力,g取10 m/s2,则( ).
玉树大地震,牵动了全国人民的心.一架装载救灾物资的直升飞机,以10 m/s的速度水平飞行,在距地面180 m的高度处,欲将救灾物资准确投放至地面目标,若不计空气阻力,g取10 m/s2,则( ).
A.物资投出后经过6 s到达地面目标
B.物资投出后经过18 s到达地面目标
C.应在距地面目标水平距离60 m处投出物资
D.应在距地面目标水平距离180 m处投出物资
解析 物资投出后做平抛运动,其落地所用时间由高度决定,t==6 s,A项正确,B项错误;抛出后至落地的水平位移为x=vt=60 m,C项正确,D项错误.
答案 AC
归纳总结:在解决平抛运动的问题时,要将平抛运动分解为水平方向的匀速直线运动和竖直方向的自由落体运动,即解决平抛运动的问题,就是解决这两个分运动的问题.只要涉及到合运动的物理量,首先要把它分解为两个分量,时间相同是两个分运动之间的联系.
三、斜面上方的平抛运动问题
![]() 例2
例2![]() 小球以15 m/s的水平初速度向一倾角为37°的斜面抛出,飞行一段时间后,恰好垂直撞在斜面上.取g=10 m/s2,tan 53°=,求:
小球以15 m/s的水平初速度向一倾角为37°的斜面抛出,飞行一段时间后,恰好垂直撞在斜面上.取g=10 m/s2,tan 53°=,求:
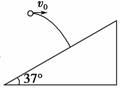
(1)小球在空中的飞行时间.
(2)抛出点距落点的高度.
解析 如图所示.由几何关系知β=90°-37°=53°.
(1)由图得tan β==,
得飞行时间t=tan β=2 s.
(2)高度h=gt2=×10×22 m=20 m.
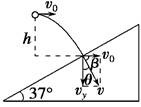
答案 (1)2 s (2)20 m
归纳总结:1.分析平抛运动,采用“化曲为直”的思想,将合运动分解为水平方向和竖直方向的两个分运动,利用平行四边形定则进行求解.
2.与斜面联系时,要充分利用斜面体的倾斜角的几何关系.
自我检测
1.关于平抛运动的说法正确的是( )
A.平抛运动是匀变速曲线运动
B.平抛物体在t时刻速度的方向与t时间内位移的方向相同
C.平抛物体在空中运动的时间随初速度增大而增大
D.若平抛物体运动的时间足够长,则速度方向将会竖直向下
解析 平抛运动的物体只受到重力作用,所以做平抛运动的物体的加速度为重力加速度,所以平抛运动是加速度恒定的变速运动,即平抛运动是匀变速曲线运动,选项A正确;平抛运动物体,t时刻的速度方向为该时刻曲线的切线方向,t时刻的位移方向为从初始位置到t时刻所在位置连线的方向,两者是不同的,选项B错误;平抛运动的时间由竖直分运动的高度h=gt2决定,即t= ,与平抛运动的水平初速度无关,选项C错误;平抛运动的速度为水平速度与竖直速度的合速度,所以平抛运动的速度不会是竖直向下,选项D错误.
答案 A
2.关于平抛运动,下列说法正确的是( )
A.平抛运动是匀变速运动
B.平抛运动是变加速运动
C.任意两段时间内加速度相同
D.任意两段相等时间内速度变化相同
解析 本题要把握好平抛运动是匀变速曲线运动及速度的矢量性,平抛运动的物体只受重力作用,故a=g,即做匀加速曲线运动,选项A正确,选项B错误,选项C正确.由匀加速运动的速度公式Δv=gΔt,所以任意相等时间内Δv相同,选项D正确.
答案 ACD
3.从离地面H高处投出A、B、C三个小球,使A球自由下落,B球以速率v水平抛出,C球以速率2v水平抛出,设三个小球落地时间分别tA、tB、tC,不计空气阻力,则下列说法正确的是( )
A.tA<tB<tC B.tA>tB>tC
C.tA<tB=tC D.tA=tB=tC
解析 三个小球在竖直方向上都做自由落体运动,由h=gt2得t= ,选项D正确.
答案 D
4.甲、乙两物体做平抛运动的初速度之比为2∶1,若它们的水平射程相等,则它们抛出点离地面的高度之比为( )
A.1∶2 B.1∶ C.1∶4 D.4∶1
解析 由x=v0t,y=gt2得x=v0,两物体水平位移x相等,则它们抛出点离地面的高度之比==,C正确.
答案 C
5.某同学对着墙壁打网球,假定球在墙面以25 m/s的速度沿水平方向反弹,落地点到墙面的距离在10 m到15 m之间,忽略空气阻力,取g=10 m/s2,球在墙面上反弹点的高度范围是( )
A.0.8 m至1.8 m B.0.8 m至1.6 m
C.1.0 m至1.6 m D.1.0 m至1.8 m
解析 由题意可知网球做平抛运动的初速度v0=25 m/s,水平位移在x1=10 m至x2=15 m之间,而水平位移x=v0t=v0·,由此得h=,代入数据得h1=0.8 m,h2=1.8 m,故A选项正确.
答案 A
6.质点从同一高度水平抛出,不计空气阻力,下列说法正确的是( )
A.质量越大,水平位移越大
B.初速度越大,落地时竖直方向速度越大
C.初速度越大,空中运动时间越长
D.初速度越大,落地速度越大
解析 物体做平抛运动时,h=gt2,x=v0t,则t=
所以x=v0,故A、C错误.
由vy=gt=,故B错误.
由v=,则v0越大,落地速度越大,故D正确.
答案 D
7.物体在高处以初速度v0水平抛出,落地时速度大小为v,那么该物体在空中运动的时间为( )
A.(v-v0)/g B.(v+v0)/g
C./g D./g
解析 把速度分解,有vy=,又因为vy=gt,可求得时间.
答案 C
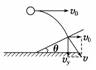
8.如图所示,以10 m/s的初速度v0水平抛出的物体,飞行一段时间后,垂直地撞在倾角θ为30°的斜面上,因此可知物体完成这段飞行的时间是( )
A. s B. s
C. s D.2 s
解析 物体做平抛运动,其可分解为水平方向的匀速直线运动和竖直方向的自由落体运动.当物体落到斜面上时,其竖直分速度vy=gt,水平分速度仍为v0.又由曲线运动的特点可知,其合速度与斜面垂直,画出速度分解的矢量平行四边形(如右图所示),由图可知:两分速度关系为vy=v0cot θ,即gt=10cot 30°,可解出t= s,故C选项正确.
答案 C
9.如图所示,从地面上方某点,将一小球以10 m/s的初速度沿水平方向抛出,小球经1 s落地,不计空气阻力,g取10 m/s2,则可求出( )
A.小球抛出点离地面的高度为5 m
B.小球抛出点到落地点的水平距离为10 m
C.小球落地点的速度大小为20 m/s
D.小球落地时的速度方向与水平地面成60°角
解析 由y=gt2,得h=gt2=×10×12 m=5 m;而水平方向上x=v0t=10×1 m=10 m;小球落地时竖直分速度vy=gt=10 m/s,则v==10 m/s;落地时速度与水平方向的夹角满足tanθ===1,即θ=45°,故A、B选项正确,C、D选项错误.
答案 AB
10.一个物体从某一确定的高度以v0的初速度水平抛出,已知它落地时的速度为vt,那么它的运动时间是( )
A. B.
C. D.
解析 平抛物体落地时的速度分解图如图所示.由图可知落地时的竖直分速度v⊥=gt,t=.
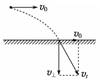
答案 D
11.小球以初速度v0与水平方向成α角斜向上抛出,不计空气阻力,球从抛出到落至与抛出点同一高度的过程中,小球速度的变化量为( )
A.v0sinα B.2v0sinα
C.v0cosα D.2v0cosα
解析 小球在整个过程中,竖直方向上满足vyt=v0sinα,由v=v0+at,得
v0sinα=-v0sinα+g·t,则t=,速度的变化量
Δv=g·t=2v0sinα故B选项正确.
答案 B
12.在490 m的高空,以240 m/s的速度水平飞行的轰炸机追击一鱼雷艇,该艇正以25 m/s的速度与飞机同方向行驶.飞机应在鱼艇后面多远处投下炸弹,才能击中该艇?
解析 从水平飞机上掷出去的炸弹,在离开飞机时具有与飞机相同的水平速度v0=240 m/s,因此炸弹做平抛运动.因为由h=490 m的高空落至水平面所需的时间t由竖直方向的分运动——自由落体运动决定,所以由公式y=gt2=h
可求出炸弹的飞行时间t= = s=10 s.
在这段时间内,炸弹在水平方向上做匀速运动,飞行的水平距离为x=v0t=240×10 m=2 400 m.
在这段时间内,鱼雷艇行驶的距离为x′=v′t=25×10 m=250 m
因为飞机与鱼雷艇运动的方向相同,所以投下的炸弹要击中鱼雷艇,飞机投弹处应在鱼雷艇后面的水平距离为
Δx=x-x′=2 400 m-250 m=2 150 m
答案 2 150 m
13.体育竞赛中的一项运动为掷镖,如图所示,墙壁上落有两只飞镖,它们是从同一位置水平射出的,飞镖A与竖直墙壁成θ1=53°角,飞镖B与竖直墙壁成θ2=37°角,两者相距为d.假设飞镖的运动为平抛运动,求射出点离墙壁的水平距离.(sin37°=0.6,cos37°=0.8)
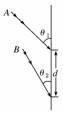
解析 设水平距离为x,飞镖的初速度为v0,落到墙壁时的竖直分速度为vy,vy==g·t,又v0=,联立以上各式可得t2=,则飞镖下落的高度h=gt2=.因此,飞镖A、B下落的高度分别为hA==、hB==,
由题意可知hB-hA=d,
即-=d,得x=d.
答案 d