专题　匀变速直线运动的位移与时间的关系  题型分析

专题一 基本公式的应用

例1 物体从静止开始做匀加速直线运动，加速度为1 m/s²，求：

(1)物体在2 s内的位移；(2)物体在第2 s内的位移；(3)物体在第二个2 s内的位移．

解析　2 s内的位移是前2 s内的位移，第2 s内的位移是第1 s末到第2 s末这1 s内的位移；第二个2 s内的位移是第2 s末到第4 s末这2 s内的位移．

由匀变速直线位移公式x＝v₀t＋at²

(1)x₁＝at＝×1×2² m＝2 m

(2)第1 s末的速度(第2 s初的速度)v₁＝v₀＋at＝1 m/s，故第2 s内位移x₂＝v₁t＋at²＝(1×1＋×1×1²) m＝1.5 m

(3)第2 s末的速度v₂＝v₀＋at′＝1×2 m/s＝2 m/s，也是物体第二个2 s的初速度，故物体在第2个2 s内的位移x₃＝v₂t′＋at′²＝(2×2＋×1×2²) m＝6 m

答案　(1)2 m　(2)1.5 m　(2)6 m

归纳总结：1．当v₀＝0时，位移公式可以简化为x＝at²应用．

2．第n s内位移的求解可用n s内的位移减去(n－1) s内的位移．

3．逆向思维法：匀减速至零的运动过程可看作初速度为零的、以原加速度反向运动的匀加速直线运动．

4．求匀减速运动的位移时要首先判定减速到零所需要的时间．

专题二 v－t图象的应用

例2 升降机由静止开始匀加速竖直上升2 s，速度达到4 m/s后，匀速竖直上升5 s，接着匀减速竖直上升3 s后停下来．求升降机在上述过程中发生的总位移x.

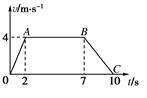
解析：　依题意，作出升降机的v－t图线，如图所示．梯形OABC的面积即等于题中所求的位移x，则x＝ m＝30 m.

答案：　30 m

归纳总结：1.利用v－t图象处理匀变速直线运动的方法

(1)选取一个过程为研究过程．

(2)分析该段图线对应的纵坐标情况分析速度，分析该段图线的倾斜程度分析加速度．

(3)利用v－t图象与时间轴所围成的面积分析物体的位移．

(4)画出运动过程v－t图象直观展现运动情况．

2．v－t图象中，在t 轴上方包围面积表示位移为正，在下方包围的面积表示位移为负.

专题三 多过程问题的分析

例3 正以30 m/s的速率运行的列车，接到前方小站的请求，在该站停靠1 min，接一个危重病人上车．司机决定以大小为0.6 m/s²的加速度匀减速运动到小站且恰在小站停下，停车1 min后以1.0 m/s²的加速度匀加速启动，恢复到原来的速度行驶．求由于临时停车，共耽误了多长时间．

解析　以列车原运动方向为正方向，设列车匀减速运动时间

为t₁，a₁＝－0.6 m/s²

由v＝v₀＋at得t₁＝＝ s＝50 s

设减速过程中行驶路程为x₁，则x₁＝v₀t₁＋a₁t＝30×50 m＋×(－0.6)×50² m＝750 m

停靠时间t₂＝60 s

设加速运动时间为t₃则由v₀＝a₂t₃得t₃＝＝ s＝30 s

加速过程中行驶路程x₂＝a₂t＝×1×30² m＝450 m

从开始制动到恢复原来速度运动共经历时间t＝t₁＋t₂＋t₃＝50 s＋60 s＋30 s＝140 s

若列车以原速度匀速驶过x＝x₁＋x₂路程，需时间t′＝＝ s＝40 s

故共耽误时间Δt＝t－t′＝140 s－40 s＝100 s

答案　100 s

专题四 推论公式的应用

例4  如图所示，某学生用打点计时器研究小车的匀变速直线运动．他将打点计时器接到频率为50 Hz的交流电源上，实验时得到一条纸带．他在纸带上便于测量的地方选取第一个计时点，在这点下标明A，第六个点下标明B，第十一个点下标明C，第十六个点下标明D，第二十一个点下标明E.测量时发现B点已模糊不清，于是他测得AC长为14.56 cm，CD长为11.15 cm，DE长为13.73 cm，则打C点时小车的瞬时速度大小为________m/s，小车运动的加速度大小为________m/s²，BC的距离应为________cm.(保留三位有效数字)

解析　由于C点是AE时间上的中点，

C的速度就等于AE段的平均速度，

v_C＝＝  ＝＝ m/s＝0.986 m/s.

又由于由A到C，C到E的时间相等，满足关系式

x_CE－x_AC＝a(2T)²，可解得

a＝＝＝ m/s²＝2.58 m/s².

由于小车做匀变速直线运动，

故x_CD－x_BC＝x_DE－x_CD，x_BC＝8.57 cm.

答案　0.986　2.58　8.57

专题五 匀变速直线运动公式的灵活选择

例5  火车沿平直铁轨匀加速前进，通过一路标时的速度为10.8 km/h,1 min后变成54 km/h，又经过一段时间，火车的速度才达到64.8 km/h.求所述过程中，火车的位移是多少？

解析　火车一直做匀加速运动，其位移可由x＝t，x＝v₀t＋at²或x＝三种不同方法求解．

v₁＝10.8 km/h＝3 m/s，v₂＝54 km/h＝15 m/s，v₃＝64.8 km/h＝18 m/s.

法一　平均速度公式法

整个过程的平均速度为：＝＝ m/s＝ m/s

由v＝v₀＋at得火车的加速度为a＝＝ m/s²＝0.2 m/s²

所以整个过程火车运动的时间为：t＝＝ s＝75 s

所以火车的位移为x＝ t＝×75 m＝787.5 m

法二　位移公式法

由x＝v₀t＋at²得x＝3×75 m＋×0.2×75² m＝787.5 m

法三　位移与速度的关系式：由v²－v＝2ax得x＝＝ m＝787.5 m.

答案　787.5 m

专题五 追及运动问题

例5 甲、乙两汽车沿同一平直公路同向匀速行驶，甲车在前，乙车在后，它们行驶的速度分别为16 m/s和18 m/s.已知甲车紧急刹车时的加速度a₁大小为3 m/s²，乙车紧急刹车时的加速度a₂大小为4 m/s²，乙车司机的反应时间为0.5 s，求为保证两车在紧急刹车过程中不相撞，甲、乙两车行驶过程中至少应保持多大距离？

解析　设甲车刹车后经时间t甲、乙两车速度相等，则16－a₁t＝18－a₂(t－0.5)，所以t＝4 s，x_甲＝16t－a₁t²＝40 m，x_乙＝18×0.5＋18×(t－0.5)－a₂(t－0.5)²＝47.5 m，Δx＝7.5 m．即甲、乙两车行驶过程中至少应保持7.5 m 距离．

答案　7.5 m

归纳总结：1．追及的特点：两个物体在同一时刻处在同一位置．

2．时间关系：从后面的物体追赶开始，到追上前面的物体时，两物体经历的时间相等．

3．位移关系：x₂＝x₀＋x₁其中x₀为开始追赶时两物体之间的距离，x₁表示前面被追物体的位移，x₂表示后面追赶物体的位移.

4．临界条件：当两个物体的速度相等时，可能出现恰好追及、恰好避免相撞，相距最远、相距最近等情况，即出现上述四种情况的临界条件为v₁＝v₂.