专题　匀变速直线运动的速度与时间的关系  题型分析

专题一 速度公式的理解及应用

例1 汽车在平直公路上以10 m/s的速度做匀速直线运动，由于接到任务，需加速前进，其加速度大小为3 m/s²，则汽车加速4 s，其速度为多大？加速5 s后呢？

解析　v₁＝v₀＋at₁＝10 m/s＋3×4 m/s＝22 m/s

v₂＝v₀＋at₂＝10 m/s＋3×5 m/s＝25 m/s.

答案　22 m/s　25 m/s

归纳总结：1．多运动过程问题要划分不同的运动阶段，并搞清各运动过程之间的联系．

2．画出运动过程的草图，标上已知量以便于灵活选用公式．

3．选取一个过程为研究过程，以初速度方向为正方向．判断各量的正负，利用v＝v₀＋at由已知条件求解未知量．

4．讨论所得矢量的大小及方向.

专题二 速度公式矢量性的应用

例2 如图所示，小球以v₀＝6 m/s 的速度从中间滑上光滑的足够长斜面，已知小球在斜面上运动时的加速度大小为2 m/s²，问小球速度大小为3 m/s时需多少时间？(小球在光滑斜面上运动时，加速度大小、方向不变)

解析　法一　当小球在上升过程中速度减为3 m/s时，以沿斜面向上的方向为正方向，此时，v₀＝6 m/s，v＝3 m/s，a＝－2 m/s²，根据v＝v₀＋at得t₁＝＝ s＝1.5 s.

小球继续向上运动，经t₂＝ s＝1.5 s速度由3 m/s减为0后，开始沿斜面向下匀加速运动；以沿斜面向下的方向为正

方向，当小球在下降过程中速度又增为3 m/s时，此时，v₀＝0，v＝3 m/s，a＝2 m/s²，

根据v＝v₀＋at得t₂′＝＝ s＝1.5 s；

综上可知，若小球在上升过程中速度达到3 m/s，则经历的时间为1.5 s；若在下降过程中速度达到3 m/s，则经历的时间为t₁＋t₂＋t₂′＝4.5 s.

法二　上滑过程达3 m/s时，同上．若在下滑过程中达到3 m/s，以沿斜面向上为正方向，则有v₀＝6 m/s，a＝－2 m/s²，v＝－3 m/s，由v＝v₀＋at得t＝4.5 s.

答案　1.5 s或4.5 s

归纳总结：1．速度公式是一个矢量表达式，速度和加速度都是矢量，可以引起多解问题．

2．小球沿斜面上、下滑动时加速度大小、方向均不变，而匀变速直线运动的速度公式的适用条件就是加速度恒定，因此对这类“双向可逆”类匀变速运动，可以全过程列式，但应注意各量的方向(正、负号)．

若在下滑过程中达到3 m/s，以沿斜面向上的方向为正方向，则有；v₀＝6 m/s，a＝－2 m/s²，v＝－3 m/s由v＝v₀＋at得t＝4.5 s.

3．对同一研究过程，各物理量正、负号选取的标准应是统一的.

专题三 v－t图象的理解及应用

例3 如图所示是某质点的v － t图象，则下列说法中正确的是(　　)．

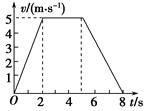
①前2 s物体做匀加速运动，后3 s物体做匀减速运动

②2～5 s内物体静止③前2 s和后3 s内速度的增量均为5 m/s

④前2 s的加速度是2.5 m/s²，后3 s的加速度是－ m/s²

A．①②　　　　B．②③　　　　C．①④　　　　D．②④

解析　物体前2 s匀加速，后3 s(5～8 s)匀减速，①对；2～5 s物体做匀速运动，②错；前2 s速度增量为5 m/s，后3 s速度增量为－5 m/s，③错；前2 s的加速度a₁＝ m/s²＝2.5 m/s²，后3 s的加速度a₂＝ m/s²＝－ m/s²，④对．

答案　C

归纳总结：1．从v－t图象可获得物体运动的信息有：

(1)物体运动快慢——对应纵轴数值．

(2)物体运动的方向——t轴上方为正方向，t轴下方为负方向．

(3)运动快慢的变化——从图线对应的v数值变化可以看出运动快慢的变化．

(4)加速度大小及变化——图线斜率大则a大，斜率小则a小．

2．图象的斜率不变，a即不变

3．利用a＝求a时，Δv＝v_t－v₀，必须是末态的速度减去初态的速度.