第三章  章末总结

要点归纳

知识点一、弹力

1．弹力产生的条件：两物体相互接触；接触面处挤压产生弹性形变。

2．影响弹力大小的因素：弹力是被动力，其大小由物体所处状态，外部对它所施加的力以及物体的形变程度决定．

3．确定弹力大小：弹簧弹力F=kx，其它的弹力利用牛顿定律和平衡条件求解。

知识点二、摩擦力

1．产生条件：①接触且挤压②接触面粗糙③有相对运动或者相对运动趋势

2．大小：滑动摩擦力,与接触面的面积无关，静摩擦力根据牛顿运动定律或平衡条件www.ks5u.com求解。www.ks5u.com

3．方向：沿接触面的切线方向，并且与相对运动或相对运动趋势方向相反

知识点三、受力分析

物体受力分析的思路

(1)明确研究对象，并将它从周围的环境中隔离出来，以避免混淆。

(2)正确画出物体受力示意图。

(3)注意防止错画力、多画力和漏画力。

知识点四、力的合成与分解

1．力的合成与分解的原理是等效替代．

2．力的合成与分解遵循的规则是平行四边形定则．

3．在力的合成中：

(1)两个共点力的合力的取值范围为|F₁－F₂|≤F≤F₁＋F₂.

(2)合力可能比分力大，也可能比分力小，也可能等于某一个分力．以两个力F₁，F₂的合力为例(θ为F₁与F₂间的夹角)：

①当θ＝0°时，F＝F₁＋F₂.②当θ＝180°时，F＝|F₁－F₂|.③当θ＝90°时，F＝.

4．在力的分解中：

(1)在分解某个力时，要根据这个力产生的实际效果进行分解．

(2)有确定解的几种常见情况：

①已知两个分力的方向，有唯一解．②已知一个分力的大小和方向，有唯一解．

③已知两个分力的大小，有唯一解．④已知一个分力的大小、另一个分力的方向(已知F₁的大小和F₂的方向，设F₂与合力F的夹角为θ)，则有

当F₁<Fsin θ时，无解；当F₁＝Fsin θ时，有唯一解；当Fsin θ<F₁<F时，有两组解；

当F₁>F时，有唯一解．

典例分析

一、胡克定律

例1 如图所示，a、b为两根相连的轻质弹簧，它们的劲度系数分别为k_a＝1×10³ N/m，k_b＝2×10³ N/m，原长分别为x_a＝6 cm，x_b＝4 cm.在下端挂一物体G，物体受到的重力为10 N，平衡时(　　)

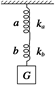
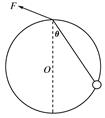
A．弹簧a下端受的拉力为4 N，b下端受的拉力为6 N

B．弹簧a下端受的拉力为10 N，b下端受的拉力为10 N

C．弹簧a的长度变为7 cm，b的长度变为4.5 cm

D．弹簧a的长度变为6.4 cm，b的长度变为4.3 cm

解析　物体被弹簧b拉住后处于静止状态，说明了弹簧对物体的拉力等于物体所受的重力．将弹簧b作为研究对象，物体拉弹簧b的拉力与弹簧a对弹簧b的拉力是一对平衡力(弹簧为轻质弹簧，即不计其重力)，所以弹簧a对弹簧b的拉力等于物体对弹簧b的拉力，大小为10 N，所以两弹簧的拉力均为10 N．由胡克定律可得k_a(x_a′－x_a)＝10 N，k_b(x_b′－x_b)＝10 N由以上两式和题设中的已知条件可得

x_a′＝7 cm，x_b′＝4.5 cm.

答案　BC

二、力的分解

例2 如图所示，一根质量不计的横梁A端用铰链固定在墙壁上，B端用细绳悬挂在墙壁上的C点，使得横梁保持水平状态．已知细绳与竖直墙壁之间的夹角为60°，当用另一段轻绳在B点悬挂一个质量为M＝6 kg的重物时，求轻杆对B点的弹力和绳BC的拉力各为多大？(g取10 m/s2)

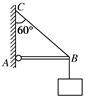
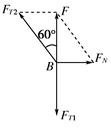
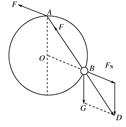
解析　设杆对B点的弹力为FN，因横梁A端用铰链固定，故FN的方向沿杆方向，绳BC对B点的拉力为F2，由于B点静止，B点所受的向下的拉力大小恒定为重物的重力，根据受力平衡的特点，杆的弹力FN与绳BC对B点的拉力FT2的合力一定竖直向上，大小为Mg，如右图所示

根据以上分析可知

弹力FN与拉力FT2的合力大小F＝FT1＝Mg＝60 N

由几何知识可知F_N＝Ftan 60°＝60 N     FT₂＝＝120 N

即轻杆对B点的弹力为60 N，绳BC的拉力为120 N.

答案：  60 N   120 N

三、图解法的应用

例3 如图所示，一定质量的物体用两根轻绳悬挂在空中，其中绳OA固定不动，绳OB在竖直平面内由水平方向向上转动，则在绳OB由水平转至竖直的过程中，绳OB的张力的大小将(　　)

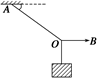
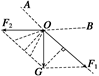
A．一直变大

B．一直变小

C．先变大后变小

D．先变小后变大

解析　这是一个动态变化问题，重力的作用效果分解在OA、OB两绳上，如右图所示，F1是对OA绳的拉力，F2是对OB绳的拉力．由于OA方向不变，当OB向上转动，转到与OA绳方向垂直时，OB上的拉力最小，故OB上的张力先变小，后变大．

答案　D

四、相识三角形

例4 如右图所示，固定在竖直平面内的光滑圆环的最高点有一个光滑的小孔．质量为m的小球套在圆环上．一根细线的下端系着小球，上端穿过小孔用手拉住．现拉动细线，使小球沿圆环缓慢上移．在移动过程中手对线的拉力F和轨道对小球的弹力FN的大小变化情况是(　　)

A．F不变，FN增大  B．F不变，FN减小 C．F减小，FN不变   D．F增大，FN减小

解析：　由长度三角形AOB与力三角形BF_ND相似，知＝＝，故F_N不变．缓慢上移时减小，F减小，故C对．

 

答案：　C

归纳总结： “相似三角形”的主要性质是对应边成比例，对应角相等．在物理中，一般当涉及矢量运算，又构建了三角形时，若矢量三角形与图中的某几何三角形为相似三角形，则可用相似三角形法解题．

五、正交分解法

例5 如下图所示，在倾角为α的斜面上，放一质量为m的小球，小球被竖直的木板挡住，不计摩擦，则球对挡板的压力是(　　)

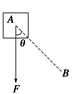
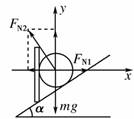
A．mgcos α　　　　　       B．mgtan α

C.                                                   D．mg

解析：　解法一　(正交分解法)：对小球受力分析如图所示，小球静止，处于平衡状态，

沿水平和竖直方向建立坐标系，将FN2正交分解，列平衡方程为FN1＝FN2sin α　mg＝FN2cos α可得：球对挡板的压力FN1′＝FN1＝mgtan α，所以B正确．