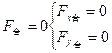|
第5节 共点力的平衡 知识点归纳 知识点一、物体的平衡 1.物体的平衡有两种情况:一是质点静止或做匀速直线运动,物体的加速度为零;二是物体不转动或匀速转动(此时的物体不能看作质点)。 2.物体的平衡的条件:静止状态和匀速直线运动。 知识点二、共点力作用下物体的平衡 1.共点力:几个力作用于物体的同一点,或它们的作用线交于同一点(该点不一定在物体上),这几个力叫共点力。 2.共点力的平衡条件:在共点力作用下物体的平衡条件是合力为零,即F合=0或Fx合=0,Fy合=0 3.判定定理:物体在三个互不平行的力的作用下处于平衡,则这三个力必为共点力。(表示这三个力的矢量首尾相接,恰能组成一个封闭三角形) 4.解题方法:当物体在两个共点力作用下平衡时,这两个力一定等值反向;当物体在三个共点力作用下平衡时,往往采用平行四边形定则或三角形定则;当物体在四个或四个以上共点力作用下平衡时,往往采用正交分解法。 5.研究三力平衡问题的常用方法 ①解析法:三角形如果有两个相互垂直,或大小相等,或有一些特殊的角度,用此法甚为简便. ②正弦定理法:三力平衡时,三个力可构成一封闭三角形,若由题设条件寻找到角度关系,则可用正弦定理列式求解. ③比例法:物体受三个力作用而处于平衡状态,若已知条件中涉及三角形的边长,则由三个力组成的矢量三角形和由边长组成的几何三角形相似,利用相似比可以方便地求解相关的问题. ④图解法:利用力的平行四边形或力的矢量三角形的边长或角度的变化关系,常常可形象、直观地分析物体所受各力的变化情况. ⑤正交分解法:处于平衡状态的物体所受到各个力的合力为零,因此可先确定研究对象,进行受力分析,然后建立直角坐标系,再根据 6.临界状态:临界状态是一种物理现象转变为另一种物理现象,或从一个物理过程转入到另一个物理过程的转折状态.临界状态也可理解为“恰好出现”或“恰好不出现”某种现象的状态.平衡物体的临界状态是指物体所处平衡状态将要变化的状态.涉及临界状态的问题称为临界问题.解决这类问题的关键是要注意“恰好出现”或“恰好不出现”的条件. 7.极值问题:极值是指研究平衡问题中某物理量变化情况时出现的最大值或最小值.中学物理的极值问题可分为简单极值问题和条件极值问题,区分的依据就是是否受附加条件限制.若受附加条件限制,则为条件极值.
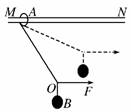
典例分析 一、物体的平衡 【例1】(1)下列哪组力作用在物体上,有可能使物体处于平衡状态 A.3N,4N,8N B.3N,5N,1N C.4N,7N,8N D.7N,9N,6N (2)用手施水平力将物体压在竖直墙壁上,在物体始终保持静止的情况下 A.压力加大,物体受的静摩擦力也加大 B.压力减小,物体受的静摩擦力也减小 C.物体所受静摩擦力为定值,与压力大小无关 D.不论物体的压力改变与否,它受到的静摩擦力总等于重力 (3)如下图所示,木块在水平桌面上,受水平力F1 =10N,F2 =3N而静止,当撤去F1后,木块仍静止,则此时木块受的合力为
A.0 B.水平向右,3N C.水平向左,7N D.水平向右,7N 解析:(1)答案:CD 在共点力作用下物体的平衡条件是合力为零,即F合=0。只有CD两个选项中的三个力合力为零。 (2)答案:CD物体始终保持静止,即是指物体一直处于平衡状态,则据共点力作用下物体的平衡条件有
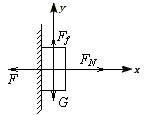
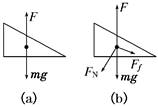
对物体受力分析,如下图
可得F = FN ,Ff = G (3)答案:A 撤去F1后,木块仍静止,则此时木块仍处于平衡状态,故木块受的合力为0. 二、正交分解法分析物体的平衡
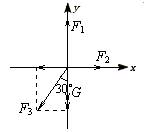
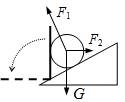
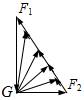
解析:气球受到四个力的作用:重力G、浮力F1、水平风力F2和绳的拉力F3,如图所示由平衡条件可得 F1=G+F3cos30° F2=F3sin30° 解得 F3= 答案:4 三、动态平衡解题 【例3】 重G的光滑小球静止在固定斜面和竖直挡板之间。若挡板逆时针缓慢转到水平位置,在该过程中,斜面和挡板对小球的弹力的大小F1、F2各如何变化?
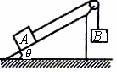
解:由于挡板是缓慢转动的,可以认为每个时刻小球都处于静止状态,因此所受合力为零。应用三角形定则,G、F1、F2三个矢量应组成封闭三角形,其中G的大小、方向始终保持不变;F1的方向不变;F2的起点在G的终点处,而终点必须在F1所在的直线上,由作图可知,挡板逆时针转动90°过程,F2矢量也逆时针转动90°,因此F1逐渐变小,F2先变小后变大。(当F2⊥F1,即挡板与斜面垂直时,F2最小) 归纳总结:力的图解法是解决动态平衡类问题的常用分析方法。这种方法的优点是形象直观。 四、平衡问题中的极值分析 【例4】跨过定滑轮的轻绳两端,分别系着物体A和物体B,物体A放在倾角为θ的斜面上(如图所示),已知物体A的质量为m ,物体A与斜面的动摩擦因数为μ(μ<tanθ),滑轮的摩擦不计,要使物体A静止在斜面上,求物体B的质量的取值范围。
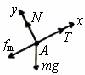
解析:先选物体B为研究对象,它受到重力mBg和拉力T的作用,根据平衡条件有: T=mBg ① 再选物体A为研究对象,它受到重力mg、斜面支持力N、轻绳拉力T和斜面的摩擦力作用,假设物体A处于将要上滑的临界状态,则物体A受的静摩擦力最大,且方向沿斜面向下,这时A的受力情况如图(乙)所示,根据平衡条件有:
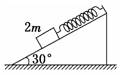
N-mgcosθ=0 ② T-fm- mgsinθ=0 ③ 由摩擦力公式知:fm=μN ④ 以上四式联立解得mB=m(sinθ+μcosθ) 再假设物体A处于将要下滑的临界状态,则物体A受的静摩擦力最大,且方向沿斜面向上,根据平衡条件有: N-mgcosθ=0 ⑤ T+fm- mgsinθ=0 ⑥ 由摩擦力公式知:fm=μN ⑦ ①⑤⑥⑦四式联立解得mB=m(sinθ-μcosθ) 综上所述,物体B的质量的取值范围是:m(sinθ-μcosθ)≤mB≤m(sinθ+μcosθ) 五、“稳态速度”类的平衡问题 【例5】当物体从高空下落时,空气阻力随速度的增大而增大,因此经过一段距离后将匀速下落,这个速度称为此物体下落的稳态速度。已知球形物体速度不大时所受的空气阻力正比于速度v,且正比于球半径r,即阻力f=krv,k是比例系数。对于常温下的空气,比例系数k=3.4×10-4Ns/m2。已知水的密度 解析:雨滴下落时受两个力作用:重力,方向向下;空气阻力,方向向上。当雨滴达到稳态速度后,加速度为0,二力平衡,用m表示雨滴质量,有mg-krv=0, 归纳总结:此题的关键就是雨滴达到“稳态速度”时,处于平衡状态。 自我检测 1.用轻弹簧竖直悬挂质量为m的物体,静止时弹簧伸长量为L.现用该弹簧沿斜面方向拉住质量为2m的物体,系统静止时弹簧伸长量也为L.斜面倾角为30°,如图所示.则物体所受摩擦力( )
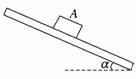
A.等于零 B.大小为mg,方向沿斜面向下 C.大小为mg,方向沿斜面向上 D.大小为mg,方向沿斜面向上 解析:由题意可知,kL=mg,物体在斜面上静止时,设受到向上的静摩擦力Ff,由平衡条件得kL+Ff=2mgsinθ,可得出Ff=0,故选A. 答案:A 2.如图所示,物块A放在倾斜的木板上,已知木板的倾角α分别为30°和45°时物块所受摩擦力的大小恰好相同,则物块和木板间的动摩擦因数为( )
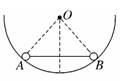
A. B. C. D. 解析:由题意可以推断出,当倾角α=30°时,物体受到的摩擦力是静摩擦力,大小为Ff1=mgsin30°,当α=45°时,物体受到的摩擦力为滑动摩擦力,大小为Ff2=μFN=μmgcos45°,由Ff1=Ff2得μ=.C项正确. 答案:C 3.如图所示,质量为m的两个球A、B固定在杆的两端,将其放入光滑的半圆形碗中,杆的长度等于碗的半径,当杆与碗的竖直半径垂直时,两球刚好能平衡,则杆对小球的作用力为( )
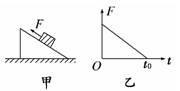
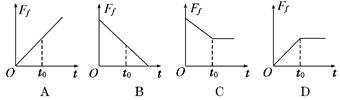
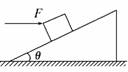
A.mg B.mg C.mg D.2mg 解析:由已知条件知,A、B间的杆一定水平,对其中一个小球受 力分析,由共点力的平衡知识可得,杆的作用力为F=mgtan30°=mg,故选项A正确. 答案:A 4.如图甲所示,一物块放在粗糙斜面上,在平行斜面向上的外力F作用下斜面和物块始终处于静止状态,当F按图乙所示规律变化时,物块与斜面间的摩擦力大小变化规律可能 是图中的( )
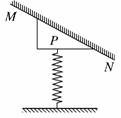
解析:依题意,若静摩擦力的方向沿着斜面向上,则有F+Ff=mgsinθ,在力F减小的过程中,Ff增大,直到力F减小到零时Ff恒定,则D可选;若静摩擦力的方向沿着斜面向下,则有F=Ff+mgsinθ,在力F减小的过程中,Ff先减小到零,然后反向增大到mgsinθ恒定,无选项对应 答案:D 5.如图所示,竖直放置的轻弹簧一端固定在地面上,另一端与斜面体P连接,P的斜面与固定挡板MN接触且处于静止状态,则斜面体P此刻所受的外力个数有可能为 ( )
A.2个 B.3个 C.4个 D.5个 解析:若斜面体P受到的弹簧弹力F等于其重力mg,则MN对P没有力的作用,如图(a)
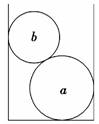
答案:AC 6.两刚性球a和b的质量分别为ma和mb,直径分别为da和db(da>db).将a、b球依次放入一竖直放置、内径为d(da<d<da+db)的平底圆筒内,如图所示.设a、b两球静止时对圆筒侧面的压力大小分别为FN1和FN2,筒底所受的压力大小为F.已知重力加速度大小为g.若所有接触都是光滑的,则 ( )
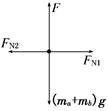
A.F=(ma+mb)g B.FN1≠FN2 C.mag<F<(ma+mb)g D.FN1=FN2 解析:对a和b整体受力分析如图所示,由平衡条件可知,F=(ma+m FN1=FN2,故A、D
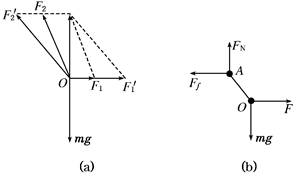
答案:AD 7.如图所示,轻绳的两端分别系在圆环A和小球B上,圆环A套在粗糙的水平直杆MN上.现用水平力F拉着绳子上的一点O,使小
A.Ff不变 B.Ff增大 C.FN减小 D.FN不变 解析:以结点O为研究对象进行受力分析.由题意可知,O点处于动态平衡,则可作出三力的平衡关系图如图(a)所示.由图可知水平拉力增大.
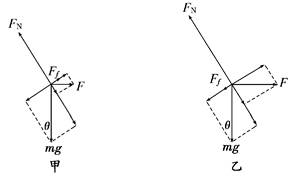
以环和结点整体作为研究对象,作受力分析图如图(b)所示.由整个系统平衡可知:FN=mg;Ff=F.即:Ff增大,FN不变,故B、D项正确. 答案:BD 8.如图所示,在倾角为θ的粗糙斜面上,有一个质量为m的物体被水平力F推着静止于斜面上,已知物体与斜面间的动摩擦因数为μ,且μ<tanθ,若物体恰好不下滑,则推力F为多少?若物体恰好不上滑,则推力F为多少?(最大静摩擦力等于滑动摩擦力)
解析:因为μ<tanθ,F=0时,物体不能静止在斜面上.当物体恰好不下滑时,受力如图甲所示,有
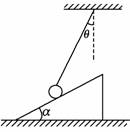
mgsinθ=Fcosθ+Ff,Ff=μFN,FN=mgcosθ+Fsinθ 解得F=mg 当物体恰好不上滑时,受力如图乙所示,有mgsinθ+Ff=Fcosθ,Ff=μFN, FN=mgcosθ+Fsinθ 解得F=mg. 答案:见解析 9.如图所示,小球被轻质细绳系住斜吊着放在静止的光滑斜面上,设小球质量m=1 kg,斜面倾角α=30°,细绳与竖直方向夹角θ=30°,光滑斜面体的质量M=3 kg,置于粗糙水平面上.(g取10 m/s2)求:(1)细绳对小球拉力的大小;(2)地面对斜面体的摩擦力的大小和方向.
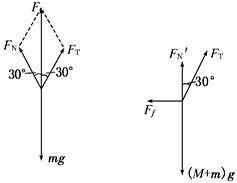
解析:(1)以小球为研究对象受力分析如图甲所示. F=mg,FTcos30°=F 得FT== N= N
(2)以小球和斜面整体为研究对象受力分析如图乙所示,因为系统静止,所以 答案:(1) N (2) N,方向水平向左 |