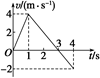第3节　匀变速直线运动的位移与时间的关系

知识点归纳

知识点一、匀速直线运动的位移

 

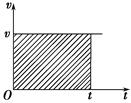
1．做匀速直线运动的物体在时间t内的位移x＝vt.

2．做匀速直线运动的物体，其v－t图象是一条平行于时间轴的直线，其位移在数值上等于v－t图线与对应的时间轴所包围的矩形的面积．如图所示：

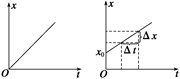
(1)v－t图象的斜率表示加速度a，在匀速直线运动中，a＝＝0.

(2)v－t图象与时间t轴间的面积在数值上等于物体做匀速直线运动在这段时间内的位移．

(3)v－t图象的纵截距表示速度的大小．

3．匀速直线运动的x－t图象

若取t＝0时，x＝0，则x－t图象为过原点的一条倾斜的直线，如图所示．

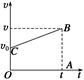
若在t＝0时，x＝x₀，则x－t图象为一条纵轴截距为x₀的倾斜的直线，如图所示，x－t图象的斜率表示物体运动的速度，v＝.

知识点二、匀变速直线运动的位移

1．匀变速直线运动的位移公式x＝v₀t＋at²

2．推导过程

如图所示，为匀变速直线运动的v－t图象，在时间t内的位移x在数值上等于图线与时间t轴所围面积．

v－t图象中直线下面的梯形OABC的面积S＝(OC＋AB)·OA

把面积以及各条线段换成所代表的物理量，得x＝(v₀＋v)t

由速度公式v＝v₀＋at代入上式得x＝v₀t＋at²

知识点三、对位移公式x＝v₀t＋at²的理解

1．适用条件：匀变速直线运动．

2．矢量性

公式x＝v₀t＋at²为矢量式，其中的x、v₀、a都是矢量，应用时必须选取统一的正方向，一般选初速度v₀的方向为正方向．

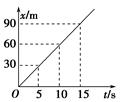
3.特殊情况

(1)x＝vt(匀速直线运动)

(2)x＝at²(由静止开始的匀加速直线运动)

知识点四、位移—时间关系图象

1．位移—时间图象(x－t图象)在平面直角坐标系中，用横轴表示时间t，用纵轴表示位移x，如图所示，根据给出(或测定)的数据，作出几个点的坐标，用平滑的直线将几个点连起来，则这条直线就表示了物体的运动特点．这种图象就叫做位移—时间图象，简称位移图象．如图所示为自行车从初始位置开始，每经过5 s的位移都是30 m的x－t图象．

2．根据x－t图象分析物体的运动

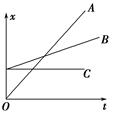
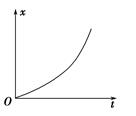
(1)由x－t图象可以确定物体各个时刻所对应的位移或物体发生一段位移所需要的时间．

(2)若物体做匀速直线运动，则x－t图象是一条倾斜的直线，如图A、B所示．直线的斜率表示物体的速度，斜率的正负表示物体的运动方向．

(3)若x－t图象为平行于时间轴的直线，表明物体处于静止状态，如图C所示．

(4)若物体做变速直线运动，x－t图象为曲线，如图所示，斜率逐渐增大，表明物体运动得越来越快．

知识点五、匀变速直线运动位移与速度的关系

1．公式推导

我们把速度公式v＝v₀＋at，变为t＝，代入位移公式x＝v₀t＋at²可得v²－v＝2ax

这就是匀变速直线运动位移与速度的关系式．

2．关系式的应用

(1)公式v²－v＝2ax是根据匀变速直线运动的两个基本关系式推导出来的，但因为不含时间变量，所以在某些问题中应用很方便．

(2)公式在应用时也必须注意符号法则，公式中的v、v₀、a、x也要规定统一的正方向，一般选初速度方向为正方向．

3．三个基本公式的选择

公式v＝v₀＋at，x＝v₀t＋at²，v²－v＝2ax中包含五个物理量，它们分别为：初速度v₀，加速度a，运动时间t，位移x和末速度v，在解题过程中选用公式的基本方法为：

(1)如果题目中无位移x，也不让求位移，一般选用速度公式v＝v₀＋at；

(2)如果题中无末速度v，也不让求末速度，一般选用位移公式x＝v₀t＋at²；

(3)如果题中无运动时间t，也不让求运动时间，一般选用导出公式v²－v＝2ax.　　

由③④得：＝v

知识点六、对位移—速度关系式的理解

1．位移与速度的关系式：v²－v＝2ax为矢量式，应用它解题时，一般先规定初速度v₀的方向为正方向：

(1)物体做加速运动时，a取正值，做减速运动时，a取负值．

(2)位移x＞0，说明物体通过的位移方向与初速度方向相同；x＜0，说明位移的方向与初速度的方向相反．

2．适用范围：匀变速直线运动．

3．特例

(1)当v₀＝0时，v²＝2ax

物体做初速度为零的匀加速直线运动．

(2)当v＝0时，－v＝2ax

物体做匀减速直线运动直到静止．

知识点七、匀变速直线运动的推论

1．平均速度：做匀变速直线运动的物体在一段时间t内的平均速度等于这段时间的中间时刻的瞬时速度，还等于这段时间初、末速度矢量和的一半．即＝v＝.

推导：设物体的初速度为v₀，做匀变速运动的加速度为a，t秒末的速度为v.由x＝v₀t＋at²得，①   平均速度＝＝v₀＋at②

由速度公式v＝v₀＋at，当t′＝时v＝v₀＋a ③

由②③得＝v④  又v＝v＋a ⑤

由③④⑤解得v＝⑥所以＝v＝.

2．逐差相等：在任意两个连续相等的时间间隔T内，位移之差是一个常量，即Δx＝x_Ⅱ－x_Ⅰ＝aT²

推导：时间T内的位移x₁＝v₀T＋aT²①

在时间2T内的位移x₂＝v₀2T＋a(2T)²②则x_Ⅰ＝x₁，x_Ⅱ＝x₂－x₁③

由①②③得Δx＝x_Ⅱ－x_Ⅰ＝aT²

此推论常有两方面的应用：一是用以判断物体是否做匀变速直线运动，二是用以求加速度．

3．某段位移中点的瞬时速度等于初速度和末速度的平方和的一半的平方根，即v＝.

4．初速度为零的匀变速直线运动的比例式(T为等时间间隔)

(1)1T末、2T末、3T末、……、nT末瞬时速度之比为v₁∶v₂∶v₃∶……∶v_n＝1∶2∶3∶……∶n

由速度公式v＝at，得v₁＝aT，v₂＝2aT，v₃＝3aT，……，v_n＝naT

所以v₁∶v₂∶v₃∶……∶v_n＝1∶2∶3∶……∶n

(2)1T内、2T内、3T内、……nT内的位移之比为x₁∶x₂∶x₃∶……∶x_n＝1²∶2²∶3²∶……∶n²

由位移公式x＝at²得x₁＝aT²，x₂＝a(2T)²，

x₃＝a(3T)²，……，x_n＝a(nT)²

所以x₁∶x₂∶x₃∶……∶x_n＝1²∶2²∶3²∶……∶n²

(3)第1个T内，第二个T内，第三个T内，……，第n个T内位移之比为

x_Ⅰ∶x_Ⅱ∶x_Ⅲ∶……∶x_n＝1∶3∶5∶……∶(2n－1)

由位移公式x＝at²得x_Ⅰ＝aT²

x_Ⅱ＝a(2T)²－aT²＝aT²

x_Ⅲ＝a(3T)²－a(2T)²＝aT²

……

x_n＝a(nT)²－a[(n－1)T]²＝aT²

所以x_Ⅰ∶x_Ⅱ∶x_Ⅲ∶……∶x_n＝1∶3∶5∶……∶(2n－1)

(4)通过连续相等的位移所用时间之比为

t₁∶t₂∶t₃∶……∶t_n＝1∶(－1)∶(－)∶……∶(－)

由x＝at²知t₁＝

通过第二段相同位移所用时间

t₂＝ － ＝ (－1)

同理t₃＝ － ＝ (－)

……

t_n＝ (－)

则t₁∶t₂∶t₃∶……∶t_n＝1∶(－1)∶(－)∶……∶(－)

 

典例分析

一、位移公式的应用

例1  一物体做匀加速直线运动，初速度为v₀＝5 m/s，加速度为a＝0.5 m/s²，求：

(1)物体在3 s内的位移；(2)物体在第3 s内的位移．

解析　(1)根据匀变速直线运动的位移公式，3 s内物体的位移x₃＝v₀t₃＋at＝5×3 m＋×0.5×3²m＝17.25 m.

(2)2 s内物体的位移x₂＝v₀t₂＋at＝(5×2＋×0.5×2²)m＝11 m

第3 s内的位移x＝x₃－x₂＝17.25 m－11 m＝6.25 m.

答案　(1)17.25 m　(2)6.25 m

归纳总结：利用位移与时间关系的公式计算位移时，首先要选出正方向，根据已知条件确定各量的符号．同时注意所求的位移是哪段时间的位移．

二、位移与速度关系式的应用

例2 美国“肯尼迪”号航空母舰上装有帮助飞机起飞的弹射系统．已知“F－15”型战斗机在跑道上加速时，产生的最大加速度为5.0 m/s²，起飞的最小速度是50 m/s，弹射系统能够使飞机具有的最大速度为30 m/s，则：

(1)飞机起飞时在跑道上至少加速多长时间才能起飞？

(2)航空母舰的跑道至少应该多长？

解析　(1)飞机在跑道上运动的过程中，当有最大初速度、最大加速度时，起飞所需时间最短，故有t＝＝ s＝4.0 s.则飞机起飞时在跑道上的加速时间至少为4.0 s.

(2)x＝＝ m＝160 m.

答案　(1)4.0 s　(2)160 m

三、v－t图象的物理意义及应用

例3 某一做直线运动的物体，其v－t图象如图所示，根据图象求：

(1)物体距出发点最远的距离；(2)前4 s内物体的位移大小；(3)前4 s内物体的路程．

解析　(1)3 s末时，物体距出发点最远，此时x_max＝×3×4 m＝6 m.

(2)前4 s内，位移x＝×3×4 m－×1×2 m＝5 m.

(3)前4 s内，路程s＝×3×4 m＋×1×2 m＝7 m.

答案　(1)6 m　(2)5 m　(3)7 m

归纳总结：v－t图象中，图线与时间轴所围面积表示位移，面积在时间轴上方表示位移为正，在时间轴下方表示位移为负，本题中0～3 s内位移为正，3～4 s内位移为负，即物体在3 s末开始反向运动.

四、刹车类问题

例4  一辆汽车以72 km/h的速度行驶，现因紧急事故急刹车并最终停止运动．已知汽车刹车过程的加速度的大小为5 m/s²，则从开始刹车经过5 s汽车通过的距离是多少？

解析　设刹车开始至汽车停止所用的时间为t₀，

选v₀的方向为正方向．v₀＝72 km/h＝20 m/s，

由v＝v₀＋at得t₀＝＝ s＝4 s

由x＝v₀t＋at²知刹车5 s内通过的距离x＝v₀t₀＋at＝20×4 m＋×(－5)×4² m＝40 m.

答案　40 m

归纳总结：汽(火)车刹车、飞机着陆等问题，物体做匀减速直线运动，停止后不再运动．这类问题的处理思路是：先求出它们从刹车到静止的刹车时间，再比较所给时间与刹车时间的关系确定运动时间，最后再利用运动公式求解．

五、追及运动问题

例5 一小汽车从静止开始以3 m/s²的加速度行驶，恰有一自行车以6 m/s的速度从车边匀速驶过．

(1)汽车从开动后到追上自行车之前，要经多长时间两者相距最远？此时距离是多少？

(2)汽车什么时候追上自行车，此时汽车的速度是多少？

解析　解法一　汽车开动后速度由零逐渐增大，而自行车速度是定值，当汽车的速度还小于自行车的速度时，两者距离越来越大，当汽车的速度大于自行车的速度时，两者距离越来越小．所以当两车的速度相等时，两车之间距离最大．

有v_汽＝at＝v_自，t＝＝2 s.

Δx＝v_自·t－at²＝6×2 m－×3×4 m＝6 m.

解法二：利用相对运动求解

以自行车为参考系，汽车追上自行车之前初速v₀＝v_汽－v_自＝0－6 m/s＝－6 m/s，加速度a＝a_汽－a_自＝3 m/s².

汽车远离自行车减速运动(与自行车对地运动方向相反)，当末速为v_t＝0时，相对自行车最远．

v_t－v₀＝at，t＝－＝ s＝2 s，v－v＝2ax，x＝－＝－6 m.

负号表示汽车比自行车落后．

解法三：极值法

设汽车在追上自行车之前经时间t相距最远．

Δx＝x_自－x_汽＝v_自·t－at²＝6t－t².

利用二次函数求极值条件知当t＝－＝ s＝2 s时，Δx最大，

故Δx_max＝6×2 m－×2² m＝6 m.

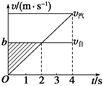
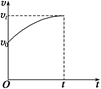
解法四：如右图所示，作出v-t图．

(2)由上图知，t=2 s以后，若两车位移相等，即v-t图象与时间轴所夹的“面积”相等．

由几何关系知，相遇时间为t′＝4 s，此时v_汽＝2v_自＝12 m/s.

答案　(1)2 s后两者相距最远，距离为6 m．　(2)4 s后追上自行车，汽车的速度为12 m/s.

自我检测

1.沿同一方向做匀加速直线运动的几个物体，比较它们在同一段时间内的位移的大小，

其中位移最大的一定是(　　)

A．这段时间的加速度最大的物体

B．这段时间的初速度最大的物体

C．这段时间的末速度最大的物体

D．这段时间的平均速度最大的物体

解析　由公式x＝v₀t＋at²＝·t＝·t知，t相同，平均速度大的物体位移大．

答案　D

2．两个小车在水平面上做加速度相同的匀减速直线运动，若它们的初速度之比为1∶2，它们运动的最大位移之比(　　)

A．1∶2            B．1∶4             C．1∶           D．2∶1

解析　x₁＝，x₂＝，所以x₁：x₂＝v：v＝1∶4.

答案　B

3．图所示为初速度为v₀沿直线运动的物体的速度图象，其末速度为v_t.在时间t内，物体的平均速度和加速度a是(　　)

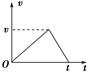
A.>，a随时间减小   B.＝，a恒定

C.<，a随时间减小   D．无法确定

答案　A

4．汽车由静止开始做匀加速直线运动，速度达到v时立即做匀减速直线运动，最后停止，运动的全部时间为t，则汽车通过的全部位移为(　　)

A.vt　　　     B.vt　　　   C.vt　　　   D.vt

解析　汽车的速度—时间图象如图所示，由于图象与时间轴所围面积等于位移，故位移x＝vt，B对．

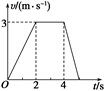
答案　B

5．用相同材料做成的A、B两木块的初速度之比为2∶3，它们以相同的加速度在同一粗糙水平面上沿直线滑行直至停止，则它们滑行的(　　)

A．时间之比为1∶1                      B．时间之比为2∶3

C．距离之比为4∶9                      D．距离之比为2∶3

解析　两木块以一定的初速度做匀减速直线运动直至停止，计算其运动时间和位移．由匀变速直线运动的速度公式v＝v₀＋at，得t＝＝－，因为加速度相同，因此运动时间之比就等于初速度之比，选项B正确；将其看成反向的初速度为零的匀加速直线运动，根据位移公式x＝at²，知位移之比等于运动时间的平方之比，选项C正确．

答案　BC

6．由静止开始做匀加速直线运动的物体，在第1 s内的位移为2 m．关于该物体的运动情况，以下说法正确的是(　　)

A．第1 s内的平均速度为2 m/s

B．第1 s末的瞬时速度为2 m/s

C．第2 s内的位移为4 m

D．运动过程中的加速度为4 m/s²

解析　由直线运动的平均速度公式＝知，第1 s内的平均速度＝＝2 m/s，A对．由x＝at²得，加速度a＝＝ m/s²＝4 m/s²，D对．第1 s末的速度v＝at＝4×1 m/s＝4 m/s，B错．第2 s内的位移x₂＝×4×2² m－×4×1² m＝6 m，C错．

答案　AD

7．如图所示的是一质点做直线运动的v－t图象，则可知(　　)

A．0～2 s与4 s～5 s内质点加速度方向相反

B．0～2 s与4 s～5 s内质点速度方向相反

C．2 s～4 s内质点加速度最大

D．0～5 s的位移为10.5 m

解析　由图象可知0～2 s内的加速度a₁＝ m/s²＝1.5 m/s²；2 s～4 s内a₂＝0；4 s～5 s内a₃＝ m/s²＝－3 m/s²，故A正确，C错．图象上0～5 s内的速度均为正值，表示速度方向都与正方向相同，故B错.0～5 s内的位移x＝ m＝10.5 m，故D正确．

答案　AD

8．一个以v₀＝5 m/s的初速度做直线运动的物体，自始至终有一个与初速度方向相反、大小为2 m/s²的加速度，则当物体位移大小为6 m时，物体已运动的时间可能为                                       (　　)

A．1 s　　　　                                      B．2 s　　　　

C．3 s　　　　                                      D．6 s

解析　当位移与v₀同向时，由x＝v₀t＋at²得6＝5t－t²，故t₁＝2 s或t₂＝3 s，B、C对．当位移与v₀方向相反时，－6＝5t－t²，故t₃＝6 s，D对．

答案　BCD

9．一辆汽车沿平直路面以15 m/s的速度行驶，紧急刹车时，做匀减速运动，加速度大小为5 m/s²，求：

(1)汽车刹车5 s时的速度；

(2)从开始刹车到停止，汽车滑行的距离．

解析　汽车刹车后做匀减速运动，初速度v₀＝15 m/s，加速度与初速度方向相反，a＝－5 m/s²，减速停止的时间为t，所以：

(1)滑行停止的时间t＝＝ s＝3 s；汽车刹车3 s时已经停止了，所以5 s时汽车的速度为零．

(2)汽车滑行的距离x＝v₀t＋at²＝15×3＋×(－5)×3² m＝22.5 m.

答案　(1)零　(2)22.5 m

10．物体做匀加速直线运动，初速度为v₀＝2 m/s，加速度为a＝0.1 m/s²，求：

(1)前4秒内的平均速度及位移；

(2)第4秒内通过的位移．

解析　(1)第4秒末的速度：

v₄＝v₀＋at＝2 m/s＋0.1×4 m/s＝2.4 m/s，

前4秒内的平均速度：＝＝ m/s＝2.2 m/s.

位移x₄＝ t＝2.2×4 m＝8.8 m.

(2)第3秒末的速度：v₃＝v₀＋at′＝2 m/s＋0.1×3 m/s＝2.3 m/s，

第4秒内通过的位移

x₄′＝t″＝×1 m＝2.35 m.

答案　(1)2.2 m/s　8.8 m　(2)2.35 m

11．一辆车以10 m/s的速度匀速行驶，在距车站25 m时开始制动，使车匀减速前进，到车站时恰好停下．求：

(1)车匀减速行驶时的加速度的大小；

(2)车从制动到停下来经历的时间．

解析　(1)由v²－v＝2ax得0－100＝2a×25，解得a＝－2 m/s²，即加速度的大小为2 m/s².

(2)车从制动到停下来经历的时间t＝＝＝5 s.

答案　(1)2 m/s²　(2)5 s

12．某种型号的飞机以60 m/s的速度着陆，着陆后飞机的运动可看做匀减速运动，加速度大小为6 m/s²，求飞机着陆后12 s 内的位移的大小．

解析　已知v₀＝60 m/s，a＝－6 m/s²，则由0＝v₀＋at得飞机停下来所需时间t＝ s＝10 s，即飞机着陆10 s后就停下来不再继续向前运动，因此12 s内的位移大小为x＝v₀t＋at²＝[60×10＋×(－6)×10²] m＝300 m.

答案　300 m