|
闭合电路的“四率”问题
【知识梳理】
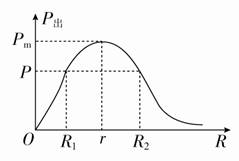
1.电源的总功率 (1)任意电路:P总=EI=U外I+U内I=P出+P内 (2)纯电阻电路:P总=I2(R+r)= 2.电源内部消耗的功率:P内=I2r=U内I=P总-P出 3.电源的输出功率 (1)任意电路:P出=UI=EI-I2r=P总-P内。 (2)纯电阻电路:P出=I2R== 讨论:如图所示 ①当R=r时,电源的输出功率最大为Pm=。 ②当R>r时,随着R的增大输出功率越来越小。 ③当R<r时,随着R的增大输出功率越来越大。 ④当P出<Pm时,每个输出功率对应两个可能的外电阻R1和R2,且R1R2=r2。
4.电源的效率 (1)任意电路:η=×100%=×100% (2)纯电阻电路:η=×100%=×100% 讨论:R越大,η越大;当R=r时,电源有最大输出功率,效率仅为50%。
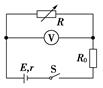
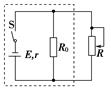
【巩固训练】 【例1】如图所示,已知电源电动势E=6 V,内阻r=1 Ω,保护电阻R0=0.5 Ω,求:当电阻箱R读数为多少时,保护电阻R0消耗的电功率最大,并求这个最大值。
[解析] 保护电阻消耗的电功率为P0=,因R0和r是常量,而R是变量,所以R最小时,P0最大,即R=0时,P0max== W=8 W。 [答案] R=0 P0max=8 W 【变式训练1】在【例1】中,条件不变,求当电阻箱R读数为多少时,电阻箱R消耗的功率PR最大,并求这个最大值。 [解析] 这时要把保护电阻R0与电源内阻r算在一起,据以上结论,当R=R0+r,即R=1 Ω+0.5 Ω=1.5 Ω时,电阻箱R消耗的功率最大,PRmax== W=6 W。 [答案] R=1.5 Ω PRmax=6 W 【变式训练2】在【例1】中,若电阻箱R的最大值为3 Ω,R0=5 Ω,求:当电阻箱R读数为多少时,电阻箱R的功率最大,并求这个最大值。 [解析] 把R0=5 Ω当作电源内阻的一部分, 则等效电源内阻r等为6 Ω,而电阻箱R的最大值为3 Ω,小于6 Ω, 由P=R=, 可知不能满足R=r等,所以当电阻箱R的电阻取3 Ω时,R消耗功率最大,最大值为:P=R= W。 [答案] R=3
Ω P= 【变式训练3】保持【例1】条件不变,求电源的最大输出功率。 [解析] 由电功率公式P出=R外=,当R外=r时,P出最大,即R=r-R0=0.5 Ω时,P出max== W=9 W。 [答案] 9 W 【变式训练4】如图所示,电源电动势E=2 V,内阻r=1 Ω,电阻R0=2 Ω,可变电阻的阻值范围为0~10 Ω。求可变电阻为多大时,R上消耗的功率最大,最大值为多少?
[解析] 法一 PR=,根据闭合电路的欧姆定律,路端电压 U=E·=, 所以PR=, 代入数据整理得PR=,当R= Ω时,R上消耗的功率最大,PRmax= W。 法二 采用等效电源法分析,把定值电阻等效到电源的内部,即把电源和定值电阻看作电动势为E′=E,内阻为r′=的电源,当R=r′=时,电源对外电路R的输出功率最大PRmax=。 把数值代入各式得:E等=E′=E= V; r等=r′== Ω。 所以PRmax== W。 [答案] R= Ω P= W
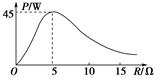
[练1]将一电源与一电阻箱连接成闭合回路,测得电阻箱所消耗功率P与电阻箱读数R变化的曲线如图所示,由此可知( )
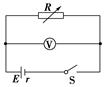
A.电源最大输出功率可能大于45 W B.电源内阻一定等于5 Ω C.电源电动势为45 V D.电阻箱所消耗功率P最大时,电源效率大于50% B [由于题述将一电源与一电阻箱连接成闭合回路,电阻箱所消耗功率P等于电源输出功率。 由电阻箱所消耗功率P与电阻箱读数R变化的曲线可知,电阻箱所消耗功率P最大为45 W,所以电源最大输出功率为45 W,选项A错误;由电源输出功率最大的条件可知,电源输出功率最大时,外电路电阻等于电源内阻,所以电源内阻一定等于5 Ω,选项B正确;由电阻箱所消耗功率P最大值为45 W可知,此时电阻箱读数为R=5 Ω,电流I==3 A,电源电动势E=I(R+r)=30 V,选项C错误;电阻箱所消耗功率P最大时,电源效率为50%,选项D错误。] [练2]如图所示电路中,R为电阻箱,
(1)求电源的电动势E和内阻r; (2)当电阻箱R读数为多少时,电源的输出功率最大?最大值Pm为多少? [解析] (1)由闭合电路的欧姆定律: E=U1+r E=U2+r 解得:E=6 V,r=1 Ω。 (2)电源的输出功率表达式:P=R 将上式变形为:P= 由上式可知R=r=1 Ω时, P取最大值:Pm==9 W。 [答案] (1)6 V 1 Ω (2)1 Ω 9 W |