第6节　反冲现象 火箭

知识点归纳

知识点一、反冲

1．定义：一个静止的物体在内力的作用下分裂为两部分，一部分向某个方向运动，另一部分必然向相反的方向运动的现象．

2．特点

(1)物体的不同部分在内力作用下向相反方向运动．

(2)反冲运动中，相互作用力一般较大，通常可以用动量守恒定律来处理．

3．反冲现象的应用及防止

(1)应用：农田、园林的喷灌装置利用反冲使水从喷口喷出时，一边喷水一边旋转．

(2)防止：用枪射击时，由于枪身的反冲会影响射击的准确性，所以用步枪射击时要把枪身抵在肩部，以减少反冲的影响．

知识点二、火箭

1．工作原理：利用反冲运动，火箭燃料燃烧产生的高温、高压燃气从尾部喷管迅速喷出，使火箭获得巨大速度．

2．影响火箭获得速度大小的两个因素

(1)喷气速度：现代火箭的喷气速度为2 000～4 000 m/s.

(2)质量比：火箭起飞时的质量与火箭除燃料外的箭体质量之比．喷气速度越大，质量比越大，火箭获得的速度越大．

知识点三、反冲运动与动量守恒定律的理解

1．反冲与动量守恒

反冲运动的产生是系统内力作用的结果，两个相互作用的物体A、B组成的系统，A对B的作用力使B获得某一方向的动量，B对A的反作用力使A获得相反方向的动量，从而使A沿着与B运动方向的相反方向运动．在以下三种情况中均可用动量守恒定律解决反冲运动问题：

(1)系统不受外力或所受外力之和为零，满足动量守恒的条件，可以用动量守恒定律解决反冲运动问题．

(2)系统虽然受到外力作用，但内力远远大于外力，外力可以忽略，也可以用动量守恒定律解决反冲运动问题．

(3)系统虽然所受外力之和不为零，系统的动量并不守恒，但系统在某一方向上不受外力或外力在该方向上的分力之和为零，则系统的动量在该方向上的分量保持不变，可以用该方向上动量守恒解决反冲运动问题．

　 2．在讨论反冲运动时应注意以下几点

(1)速度的反向性：若系统原来静止，抛出部分具有速度时，剩余部分的反冲是相对于抛出部分而言的，两者速度方向相反．可任意规定某一部分的运动方向为正方向，列出动量守恒方程．质量为M的物体以对地速度v抛出一个质量为m的物体，研究剩余部分(M－m)对地反冲速度时，设v的方向为正．

列出的方程式为 mv＋(M－m)v′＝0，得v′＝－v.

由于v′为待求速度，事先可不考虑其方向，由计算结果为负值，表示剩余部分的运动方向与抛出部分速度方向相反．

由于我们已明确剩余部分与抛出部分反向，因此可直接列出两部分动量大小相等方程．即上例可列式为mv＝(M－m)v′，v′＝ v

其中v′为剩余部分的速率．

(2)速度的相对性

在反冲运动中，若已知条件是物体间的相对速度，利用动量守恒定律列方程时，应将相对速度转化为绝对速度(一设为对地速度)．

知识点四、“人船模型”的处理方法

1．“人船模型”问题的特征

两个原来静止的物体发生相互作用时，若所受外力的矢量和为零，则动量守恒．在相互作用的过程中，任一时刻两物体的速度大小之比等于质量的反比．这样的问题归为“人船模型”问题．

2．处理“人船模型”问题的关键

(1)利用动量守恒，确定两物体速度关系，再确定两物体通过的位移的关系．

由于动量守恒，所以任一时刻系统的总动量为零，动量守恒式可写成m₁v₁＝m₂v₂的形式(v₁、v₂为两物体的瞬时速率)，表明任意时刻的瞬时速率都与各物体的质量成反比．所以全过程的平均速度也与质量成反比．进而可得两物体的位移大小与各物体的质量成反比，即＝.

(2)解题时要画出各物体的位移关系草图，找出各长度间的关系．

典例分析

一、火箭原理

例1 运送人造地球卫星的火箭开始工作后，火箭做加速运动的原因(   )

A．燃料推动空气，空气的反作用力推动火箭

B．火箭发动机用力将燃料燃烧产生的气体向后推出，气体的反作用力推动火箭

C．火箭吸入空气，然后向后排出，空气对火箭的反作用力推动火箭

D．火箭燃料燃烧发热，加热周围空气，空气膨胀推动火箭

解析 火箭的工作原理是利用反冲运动，是火箭燃料燃烧产生的高温高压燃气从尾喷管喷出时，使火箭获得反冲速度，故正确答案为选项 B.

答案 B

二、人船模型

例2 质量为M的热气球吊筐中有一质量为m的人，共同静止在距地面为h的高空中．现从气球上放下一根质量不计的软绳，为使此人沿软绳能安全滑到地面，则软绳至少有多长？

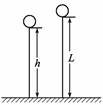
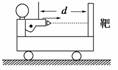
解析　如图所示，设绳长为L，人沿软绳滑至地面的时间为t，由图可知，L＝x_人＋x_球．设人下滑的平均速度大小为v_人，气球上升的平均速度大小为v_球，由动量守恒定律得：0＝Mv_球－mv_人即0＝M－m，0＝Mx_球－mx_人

又有x_人＋x_球＝L，x_人＝h

联立以上各式得：L＝h.

答案　h

自我检测

1．下列不属于反冲运动的是(　　)

A．喷气式飞机的运动       B．直升机的运动

C．火箭的运动             D．反击式水轮机的运动

解析 喷气式飞机和火箭都是靠喷出气体，通过反冲获得前进的动力；反击式水轮机靠水轮击打水，通过反冲获得动力；直升机运动是飞机螺旋桨与外部空气作用的结果，不属于反冲运动．

答案 B

2．采取下列哪些措施有利于增加火箭的飞行速度(　　)

A．使喷出的气体速度增大      B．使喷出的气体温度更高

C．使喷出的气体质量更大      D．使喷出的气体密度更小

解析 设原来火箭的总质量为M，喷出的气体质量为m，速度是v，剩余的质量(M－m)的速度是v′，由动量守恒得出：(M－m)v′＝mv得：v′＝＝，由该式可知：m越大，v越大，v′越大．故A、C正确．

答案 AC

3．质量相等的甲和乙都静止在光滑的水平冰面上．现在，其中一人向另一个人抛出一个篮球，另一人接球后再抛回．如此反复进行几次后，甲和乙最后的速率关系是(　　)

A．若甲最先抛球，则一定是v_甲>v_乙

B．若乙最后接球，则一定是v_甲>v_乙

C．只有甲先抛球，乙最后接球，才有v_甲>v_乙

D．无论怎样抛球和接球，都是v_甲>v_乙

解析　因甲、乙及篮球组成的系统动量守恒，故最终甲、乙以及篮球的动量之和必为零．根据动量守恒定律有m₁v₁＝(m₂＋m_球)v₂，因此最终谁接球谁的速度小，故B正确，ACD错误．

答案　B

4．一炮艇总质量为M，以速度v₀匀速行驶，从艇上以相对海岸的水平速度v沿前进方向射出一质量为m的炮弹，发射炮弹后艇的速度为v′，若不计水的阻力，则下列各关系式中正确的是(　　)

A．Mv₀＝(M－m)v′＋mv             B．Mv₀＝(M－m)v′＋m(v＋v₀)

C．Mv₀＝(M－m)v′＋m(v＋v′)       D．Mv₀＝Mv′＋mv

解析 动量守恒定律必须相对于同一参考系．本题中的各个速度都是相对于地面的，不需要转换．发射炮弹前系统的总动量为Mv₀；发射炮弹后炮弹的动量为mv，船的动量为(M－m)v′，所以动量守恒定律的表达式为Mv₀＝(M－m)v′＋mv，选项A正确．

答案 A

5．假设一个小型宇宙飞船沿人造地球卫星的轨道在高空中绕地球做匀速圆周运动，如果飞船沿其速度相反的方向抛出一个质量不可忽略的物体A，则下列说法正确的是(　　)

A．A与飞船都可能沿原轨道运动

B．A与飞船都不可能沿原轨道运动

C．A运动的轨道半径可能减小，也可能增加

D．A可能沿地球半径方向竖直下落，而飞船运行的轨道半径将增大

解析 抛出物体A后，由反冲原理知飞船速度变大，所需向心力变大，从而飞船做离心运动离开原来轨道，半径增大；物体A的速率可能比原来的速率大，也可比原来的速率小或相等，也可能等于零从而竖直下落。

答案 BCD

6．质量为m的人，原来静止在乙船上，甲、乙两船质量均为M，开始时都静止，人先跳到甲船，立即再跳回乙船，这时两船速度大小之比为v_甲∶v_乙等于(　　)

A. 1∶1　　　　　　　　　　B．m∶M

C．(m＋M)∶M             D．m∶(M＋m)

解析  对人及甲、乙两船，由动量守恒定律得：Mv_甲－(M＋m)v_乙＝0，

即v_甲∶v_乙＝(m＋M)∶M.

故C正确．

答案 C

7．假设一个小型宇宙飞船沿人造地球卫星的轨道在高空中绕地球做匀速圆周运动，如果飞船沿其速度相反的方向抛出一个质量不可忽略的物体A，则下列说法正确错误的是(　　)

A．A与飞船都可能沿原轨道运动

B．A与飞船都不可能沿原轨道运动

C．A运动的轨道半径可能减小，也可能增加

D．A可能沿地球半径方向竖直下落，而飞船运行的轨道半径将增大

解析 抛出物体A后，由反冲原理知飞船速度变大，所需向心力变大，从而飞船做离心运动离开原来轨道，半径增大；物体A的速率可能比原来的速率大，也可比原来的速率小或相等，也可能等于零从而竖直下落．

答案 A

8.某学习小组在探究反冲运动时，将质量为m₁的一个小液化气瓶固定在质量为m₂的小玩具船上，利用液化气瓶向外喷射气体作为船的动力。现在整个装置静止放在平静的水面上，已知打开瓶后向外喷射气体的对地速度为v₁，如果在Δt的时间内向后喷射的气体的质量为Δm，忽略水的阻力，则喷射出质量为Δm的气体后，小船的速度是多少？

解析 由动量守恒定律得：(m₁＋m₂－Δm)v_船－Δmv₁＝0

得：v_船＝。

答案

9．课外科技小组制作一只“水火箭”，用压缩空气压出水流使火箭运动。假如喷出的水流流量保持为2×10^－4m³/s，喷出速度保持为对地10m/s。启动前火箭总质量为1.4kg，则启动2s末火箭的速度可以达到多少？已知火箭沿水平轨道运动阻力不计，水的密度是10³kg/m³。

解析 “水火箭”喷出水流做反冲运动，设火箭原来总质量为M，喷出水流的流量为Q，水的密度为ρ，水流的喷出速度为v，火箭的反冲速度为v′，由动量守恒定律得

(M－ρQt)v′＝ρQtv

火箭启动后2s末的速度为v′＝＝m/s＝4m/s

答案 4m/s

10.小车静置在光滑水平面上，站在车上的人练习打靶，人站在车的一端，靶固定在车的另一端，枪离靶的距离为d，如图所示。已知车、人、靶和枪的总质量为M(不包括子弹)，每颗子弹质量为m，共n发，每颗子弹击中靶后，就留在靶内，且待前一发击中靶后，再打下一发。打完n发后，小车移动的距离为多少？

 

解析 由题意知系统动量守恒，前一发击中靶后，再打下一发，说明发射后一颗子弹时，车已经停止运动。每发射一颗子弹，车后退一段距离。每发射一颗子弹时，子弹动量为mv，由动量守恒定律有：

0＝mv－[M＋(n－1)m]V

mv＝[M＋(n－1)m]V

设每发射一颗子弹车后退x，则子弹相对于地面运动的距离是(d－x)，由动量守恒定律有：m()＝[M＋(n－1)m]

解得：x＝，则打完n发后车共后退s＝。

答案 s＝