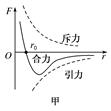
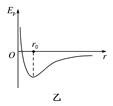
第一章  章末总结

要点归纳

知识点一、阿伏加德罗常数的相关计算

1．已知物质的摩尔质量M，借助于阿伏加德罗常数N_A，可以求得这种物质的分子质量m₀＝.

2．已知物质的摩尔体积V_A，借助于阿伏加德罗常数N_A，可以计算出这种物质的一个分子所占据的体积V₀＝.

3．若物体是固体或液体，可把分子视为紧密排列的球形分子，可估算出分子直径d＝ .

4．依据求得的一个分子占据的体积V₀，可估算分子间距，此时把每个分子占据的空间看作一个小立方体模型，所以分子间距d＝，这对气体、固体、液体均适用．

5．已知物体的体积V和摩尔体积V_A，求物体的分子数N，则N＝.

6．已知物体的质量m和摩尔质量M，求物体的分子数N，则N＝N_A.

知识点二、分子力曲线和分子势能曲线的比较和应用

比较如下：

知识点三、物体的内能、分子热运动

1．物体的内能与分子动能、分子势能：

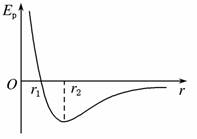
2.分子热运动：分子热运动是永不停息无规则的，温度越高越剧烈．大量分子的运动符合统计规律．例如，温度升高，分子的平均动能增加．单个分子的运动没有规律，也没有实际意义．

典例分析

一、阿伏伽德罗常数的计算

【例1】已知金刚石的密度为ρ＝3.5×10³ kg/m³，现有体积为4.0×10^－8 m³的一小块金刚石，它有多少个碳原子？假如金刚石中的碳原子是紧密地挨在一起的，试估算碳原子的直径．(保留两位有效数字)

解析　先求金刚石的质量：m＝ρV＝3.5×10³×4.0×10^－8 kg＝1.4×10^－4 kg

这块金刚石的摩尔数：n＝＝≈1.17×10^－2 mol

这块金刚石所含的碳原子数：N＝nN_A＝1.17×10^－2×6.02×10²³≈7.0×10²¹(个)

一个碳原子的体积：V₀＝＝ m³＝5.7×10^－30 m³

把金刚石中的碳原子看成球体，则由公式V₀＝d³可得碳原子直径：

d＝ ＝ m＝2.2×10^－10 m

答案　7.0×10²¹个　2.2×10^－10 m

归纳总结：(1)牢牢抓住阿伏加德罗常数，它是联系微观物理量和宏观物理量的桥梁；

(2)注意理想模型的建立：对于固体和液体，可以认为它们的分子是一个挨一个紧密排列的，分子之间没有空隙，设分子体积为V0，则分子的直径d＝2r＝(球体模型)或d＝(立方体模型)；对于气体，分子间有一个很大的空隙，一般建立立方体模型，求出的立方体边长是两个相邻的气体分子之间的平均距离，并非气体分子的大小，即d＝.

(3)估算时，要灵活地用好阿伏加德罗常数这个桥梁．

二、分子力、分子势能与分子间距离的关系

【例2】如图所示为一分子势能随距离变化的图线，从图中分析可得到(　　)

A．r₁处为分子的平衡位置

B．r₂处为分子的平衡位置

C．r→∞处，分子间的势能为最小值，分子间无相互作用力

D．若r<r₁，r越小，分子间势能越大，分子间仅有斥力存在

解析　当分子处于平衡位置时，分子力为零，分子势能最小，A、C错误，B正确；若r<r₁，r越小，分子间势能越大，分子间的引力和斥力都越大，D错误．

答案　B

归纳总结：(1)分子力的变化由分子力与分子间距的关系图判断；

(2)分子势能在平衡位置有最小值，无论分子间距离如何变化，靠近平衡位置，分子势能减小，反之增大；

(3)判断分子势能的变化有两种方法：①看分子力做功情况；②直接由分子势能与分子间距离的关系图线判断，但要注意r＝r0是分子势能最小的点．

三、内能

【例3】下列说法中正确的是(　　)

A．物体温度降低，其分子热运动的平均动能增大

B．物体温度升高，其分子热运动的平均动能增大

C．物体温度降低，其内能一定增大

D．物体温度不变，其内能一定不变

解析　根据温度是分子平均动能的标志知，温度升高，分子热运动的平均动能增大；温度降低，分子热运动的平均动能减小，选项A错误，B正确．理想气体的温度升高，内能增大；温度降低，内能减小，选项C错误．晶体熔化或凝固时温度不变，但是内能变化，熔化时吸收热量，内能增大；凝固时放出热量，内能减小，选项D错误．

答案　B