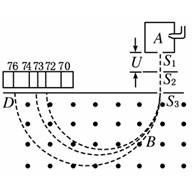
第4节　质谱仪与回旋加速器

知识点归纳

知识点一、质谱仪

①构造：如图所示，由粒子源、加速电场、偏转磁场和照相底片等构成。

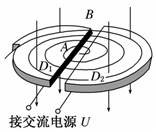
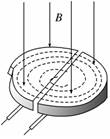
②原理：粒子由静止被加速电场加速，根据动能定理可得：mv²＝qU。①

粒子在磁场中做匀速圆周运动，根据牛顿第二定律得：qvB＝m。②

由①②两式可得比荷：＝。

知识点二、回旋加速器

1．工作原理： 交流电的周期和粒子做圆周运动的周期相等，粒子在圆周运动的过程中一次一次地经过D形盒缝隙，两盒间的电势差一次一次地反向，粒子就会被一次一次地加速。由qvB＝，得E_km＝，可见粒子获得的最大动能由磁感应强度B和D形盒半径R决定，与加速电压无关。

(1)磁场的作用：带电粒子以某一速度垂直磁场方向进入匀强磁场后，在洛伦兹力作用下做匀速圆周运动，其周期与速率、半径均无关(T＝)，带电粒子每次进入D形盒都运动相等的时间(半个周期)后平行电场方向进入电场中加速。

(2)电场的作用：回旋加速器两个D形盒之间的窄缝区域存在周期性变化的并垂直于两D形盒正对截面的匀强电场，带电粒子经过该区域时被加速。

  (3)交变电压：为保证带电粒子每次经过窄缝时都被加速，使之能量不断提高，需在窄缝两侧加上跟带电粒子在D形盒中运动周期相同的交变电压。

2．带电粒子的最终能量

当带电粒子的速度最大时，其运动半径也最大，由r＝得v＝，若D形盒半径为R，则带电粒子的最终动能E_m＝。可见，要提高加速粒子的最终能量，应尽可能增大磁感应强度B和D形盒的半径R。

典例分析

一、质谱仪

例1 有一种质谱仪的结构如下图所示．带电粒子经过S1和S2之间的电场加速后，进入P1、P2之间的狭缝．P1、P2之间存在着互相正交的磁场B1和电场E，只有在这一区域内不改变运动方向的粒子才能顺利通过S0上的狭缝，进入磁感应强度为B2的匀强磁场区域后做匀速圆周运动，打在屏A′A上，并发出亮光，记录下亮光所在的位置，量取狭缝到亮光的距离d，即可求出带电粒子的荷质比，简述其原理．

解析 设加速电场加速电压为U，可求得带电粒子进入速度选择器时的速度v，根据平衡条件知道，只有速度为v的带电粒子才能被选择．粒子做匀速圆周运动时，根据洛伦兹力充当向心力，建立q/m的关系即可求解，由qvB1＝qE可知，只有速度为：v＝E/B1的粒子才能通过．这一部分装置叫速度选择器，S0以下的空间只存在磁场B2，不存在电场．带电粒子在洛伦兹力的作用下将做半径为R(R＝)的匀速圆周运动．

qvB2＝mv2/R                      ①

qB2＝mE/B1R                                   ②

由②得式中B1、B2是人为加上去的，R可测量，这样便可以求带电粒子的荷质比q/m.

归纳总结：质谱仪的主要原理是带电粒子在磁场中的偏转，在现代科学技术中有着重要作用．处理这类习题时要注意对带电粒子运动过程的分析．

二、回旋加速器

例2  如图所示，回旋加速器是用来加速带电粒子使它获得很大动能的装置，其核心部分是两个D形金属盒，置于匀强磁场中，两盒分别与高频电源相连。如果D形金属盒的半径为R，垂直D形金属底面的匀强磁场的磁感应强度为B，高频电源频率为f，下列说法中不正确的是(　　)

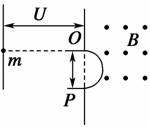
A．质子被加速后的最大速度不可能超过2πfR

B．质子被加速后的最大速度与加速电场的电压大小无关

C．高频电源只能使用矩形波交变电流，不能使用正弦式交变电流

D．要想用这个装置加速α粒子(电荷量为质子的2倍，质量为质子的4倍)，必须改变交变电流的频率

解析 质子在D形金属盒内做匀速圆周运动的周期T＝，所加高频交变电流的频率f＝，所以质子的最大速度v_m＝wR＝2πfR，A项正确；由v_m＝2πfR可知，质子被加速的最大速度与加速电场的电压大小无关，与交变电流的波形无关，B项正确，C项错误；由T＝可知，被加速粒子运动的周期与粒子的比荷有关，只有在改变高频交变电流的频率后才能用于加速α粒子，D项正确。

答案 C

归纳总结：(1)带电粒子垂直进入匀强磁场时，带电粒子在磁场中只受洛伦兹力做匀速圆周运动，带电粒子的周期T=，与速度大小无关，只与有关系，圆周运动的半径R=，与速度成正比。

(2)处理带电粒子在磁场中的圆周运动问题，通常先确定圆心，画出轨迹草图，结合几何知识确定轨迹半径，然后利用洛伦兹力充当向心力列出方程求解。

(3) 在回旋加速器中被加速粒子的最终能量由磁感应强度的大小和D形盒的最大半径决定。

自我检测

1．质谱仪的两大重要组成部分是加速电场和偏转磁场，如图为质谱仪的原理图．设想有一个静止的质量为m、带电量为q的带电粒子 (不计重力)，经电压为U的加速电场加速后垂直进入磁感应强度为B的偏转磁场中，带电粒子打至底片上的P点，设OP＝x，则在图中能正确反映x与U之间的函数关系的是(　　)

          

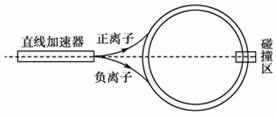
解析 带电粒子先经加速电场加速，故qU＝mv²，进入磁场后偏转，OP＝x＝2r＝，两式联立得，OP＝x＝∝，所以B为正确答案．

答案 B

2．环形对撞机是研究高能离子的重要装置，如图正、负离子由静止经过电压为U的直线加速器加速后，沿圆环切线方向注入对撞机的真空环状空腔内，空腔内存在着与圆环平面垂直的匀强磁场，磁感应强度大小为B.(两种带电粒子将被局限在环状空腔内，沿相反方向做半径相等的匀强圆周运动，从而在碰撞区迎面相撞．)为维持带电粒子在环状空腔中的匀速圆周运动，下列说法正确的是(　　)

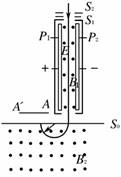
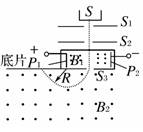
A．对于给定的加速电压，带电粒子的比荷越大，磁感应强度B越大

B．对于给定的加速电压，带电粒子的比荷越大，磁感应强度B越小

C．对于给定的带电粒子，加速电压U越大，粒子运动的周期越小

D．对于给定的带电粒子，不管加速电压U多大，粒子运动的周期都不变

解析 在加速器中qU＝mv²，在环状空腔内做匀速圆周运动的半径r＝，即r＝，所以在半径不变的条件下越大，B越小，选项B正确；粒子在空腔内的周期T＝，故加速电压越大，粒子的速率v越大，其周期越小，选项C正确．

答案 BC

3．如下图所示，是一种质谱仪的示意图，从离子源S产生的正离子，经过S₁和S₂之间的加速电场，进入速度选择器，P₁和P₂间的电场强度为E，磁感应强度为B₁，离子由S₃射出后进入磁感应强度为B₂的匀强磁场区域，由于各种离子轨迹半径R不同，而分别射到底片上不同的位置，形成谱线．

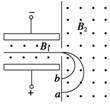
(1)若已知S₁S₂间加速电压为U，并且磁感应强度B₂半径R也是已知的，则离子的比荷__________.

(2)若已知速度选择器中的电场强度E和磁感应强度B₁，R和B₂也知道，则离子的比荷为______________．

(3)要使氢的同位素氘和氚经加速电场和速度选择器以相同的速度进入磁感应强度为B₂的匀强磁场．(设进入加速电场时速度为零)

A．若保持速度选择器的E和B₁不变，则加速电场S₁S₂间的电压比应为________________．

B．它们谱线位置到狭缝S₃间距离之比为____________________．

解析 (1)由于粒子在B₂区域做匀速圆周运动，R＝，这个速度也就是粒子经加速电场加速后的速度，在加速过程中qU＝mv²，所以＝＝，＝

(2)在速度选择器中，粒子沿直线穿过，故qE＝qvB₁

E＝vB₁＝，故＝

(3)(A)氘核H，氚核H，设经加速后二者速度均为v，经电场加速：q₁U₁＝m₁v²，q₂U₂＝m₂v².

由以上两式得：＝＝·＝

(B)它们谱线的位置到狭缝S₃的距离之比实际上就是两种粒子在磁场中做匀速圆周运动的直径之比，也是半径之比．＝＝＝＝.

答案 (1)　(2)　(3)A.；B.

4．一回旋加速器，在外加磁场一定时，可把质子(H)加速到v，使它获得动能为E_k，则：

(1)能把α粒子(He)加速到的速度为________．

(2)能使α粒子获得的动能为________．

(3)加速α粒子的交流电压频率与加速质子的交流电压频率之比为________．

解析：应用粒子在磁场中做圆周运动的半径公式和周期公式便可求出速度的表达式及频率表达式．

(1)设加速器D形盒半径为R，磁场磁感应强度为B

由R＝得v＝，＝×＝×＝

所以α粒子获得的速度v_α＝v_p＝v.

(2)由动能E_k＝mv²，得

＝()²×＝()²×＝

所以α粒子获得的动能也为E_k.

(3)交流电压频率与粒子在磁场中的回旋频率相等

f＝＝，＝×＝×＝.

α粒子与质子所需交流电压频率之比为1∶2.

答案：(1)　(2)E_k　(3)1∶2

5．质谱仪是用来测定带电粒子的质量和分析同位素的装置，如图所示，电容器两极板相距为d，两板间的电压为U，极板间的匀强磁场的磁感应强度为B₁，一束电荷量相同的带正电的粒子沿电容器的中线平行于极板射入电容器，沿直线穿过电容器后进入另一磁感应强度为B₂的匀强磁场，结果分别打在感光片上的a、b两点，设a、b两点之间的距离为x，粒子所带电荷量为q，如不计重力．求：

(1)粒子进入匀强磁场B₂时的速度v为多少？

(2)打在a、b两点的粒子的质量之差Δm为多少？

解析　(1)粒子在电容器中做直线运动，故q＝qvB₁，得v＝.

(2)带电粒子在匀强磁场B₂中做匀速圆周运动，则打在a处的粒子的轨道半径R₁＝，打在b处的粒子的轨道半径R₂＝，又x＝2R₁－2R₂，解得Δm＝m₁－m₂＝.

答案　(1)　(2)