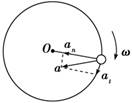
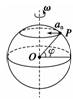
第3节　向心加速度

知识点归纳

知识点一、向心加速度

1．速度变化量．

(1)定义：运动的物体在一段时间内的末速度与初速度之差．

(2)表达式：Δv＝v末－v初

2．向心加速度．

(1)定义：任何做匀速圆周运动的物体的加速度都指向圆心，这个加速度叫做向心加速度．

(2)方向：向心加速度的方向总是沿着半径指向圆心，跟该点的线速度方向垂直．向心加速度的方向时刻在改变．

(3)大小：an＝.根据v＝ωr可得an＝ω2r.

(4)物理意义：向心加速度是描述线速度方向改变快慢的物理量．向心加速度是由于线速度的方向改变而产生的，因此线速度的方向变化的快慢决定了向心加速度的大小．

3．向心加速度不同形式的各种表达式

(1)对应线速度：an＝.

(2)对应角速度：an＝rω².

(3)对应周期：an＝r.

(4)对应转速：an＝4π²n²r.

(5)推导公式：an＝ωv.

4．非匀速圆周运动的加速度．

做非匀速圆周运动的物体的加速度并不指向圆心，而是与半径有一个夹角，我们可以把加速度a分解为沿半径方向的an和沿切线方向的at，如图所示，则an描述速度方向改变的快慢，at描述速度大小改变的快慢，其中an就是向心加速度．

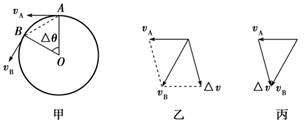
知识点二、向心加速度的方向和大小

1．向心加速度的推导．

(1)情景设置：

我们可以先把有关速度矢量vA和vB画成图(甲)所示，图中vA、vB分别表示做匀速圆周运动的物体

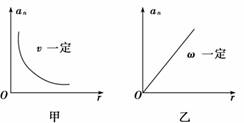
在A、B两点时的速度．作出图(乙)所示的平行四边形，这个平行四边形可理解为将速度vA和速度的变化量Δv合成得到vB.它也能用图(丙)所示的三角形法则来表示，同样可以看成vA与Δv合成得到vB.这就是说从vA变到vB，发生了Δv的变化，从而求出速度矢量的改变量Δv＝vB－vA.

(2)推理：

当Δt→0时，Δv的方向是沿半径指向圆心的，所以加速度的方向也是时刻指向圆心的．

因为v_A、v_B和Δv组成的三角形与△OAB是相似三角形，所以＝，即Δv＝，将上式两边同时除以Δt，得＝×.当Δt→0时，弦AB近似等于弧长，所以等于圆周运动的线速度v，从而得出a＝＝.将v＝ωr代入上式可得a＝ω²r.

2．向心加速度的方向：总是沿着半径指向圆心，即方向始终与运动方向垂直．由于向心加速度始终与速度垂直，故向心加速度只改变速度的方向，不改变速度的大小，向心加速度的大小表示速度方向改变的快慢．

知识点三、向心加速度的大小与半径是的关系以及与合加速度的关系

1．向心加速度与半径的关系．

在表达式an＝＝ω2r中，an与两个量(ω或v、r)有关，在讨论时要注意用控制变量法分析：若角速度ω相同，a∝r；若线速度v大小相同，a∝.

an与r的关系可用图甲、乙表示．

2．向心加速度与合加速度的关系．

(1)物体做匀速圆周运动时，向心加速度就是物体运动的合加速度．

(2)物体做非匀速圆周运动时，合加速度必有一个沿切线方向的分量和指向圆心方向的分量，其指向圆心方向的分量就是向心加速度，此时向心加速度仍满足an＝＝ω2r.

典例分析

一、位移公式的应用

例1  一物体做匀加速直线运动，初速度为v₀＝5 m/s，加速度为a＝0.5 m/s²，求：

 

一、对向心加速度的理解

例1  关于向心加速度，下列说法正确的是   (　　)．

A．向心加速度是描述线速度大小变化快慢的物理量

B．向心加速度是描述线速度的方向变化快慢的物理量

C．向心加速度时刻指向圆心，方向不变

D．向心加速度是平均加速度，大小可用a＝来计算

解析　加速度是描述速度变化快慢的物理量，向心加速度是描述线速度方向变化快慢的物理量，因此A错、B对．虽然向心加速度时刻指向圆心，但是沿不同的半径指向圆心，所以方向不断变化，C错．加速度公式a＝适用于平均加速度的计算，向心加速度是瞬时加速度，D错．

答案　B

归纳总结：深刻理解向心加速度的物理意义是描述速度方向改变快慢的，方向始终指向圆心，所以它是变量.

二、对向心加速度的表达式的理解

例2  一物体以12 m/s的线速度做匀速圆周运动，转动周期为3 s，则物体在运动过程中的任一时刻，速度变化率的大小为(　　)

A. m/s²                                                       B．8 m/s² 

C．0                                                              D．8π m/s²

解析　由于物体的线速度v＝12 m/s，角速度ω＝＝rad/s.所以它的速度变化率a_n＝v ω＝12× m/s²＝8π m/s²，D对．

答案　D

归纳总结：由an＝＝ω²r分析，an究竟与半径成正比还是成反比，要看清是v一定还是ω一定.

三、传动装置的向心加速度的计算

例2 如图所示，O、O1为两个皮带轮，O轮的半径为r，O1轮的半径为R，且R>r，M点为O轮边缘上的一点，N为O1轮上的任意一点，当皮带轮转动时，(设转动过程不打滑)则(　　)

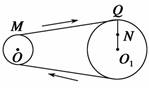
A．M点的向心加速度一定大于N点的向心加速度

B．M点的向心加速度一定等于N点的向心加速度

C．M点的向心加速度可能小于N点的向心加速度

D．M点的向心加速度可能等于N点的向心加速度

解析　Q点和N点在同一个轮子上，其角速度相等，即ω_Q＝ω_N，又r_Q>r_N，由向心加速度公式a_n＝ω²r可知a_Q>a_N；由于皮带转动时不打滑，Q点和M点都在由皮带传动的两个轮子边缘，这两点的线速度大小相等，即v_Q＝v_M，又r_Q>r_M，由向心加速度公式a_n＝可知a_Q<a_M，所以a_M>a_N，选项A正确．

答案　A

归纳总结：分析传动问题关键有两点：其一是同一轮上的各点角速度相同；其二是皮带不打滑时，与皮带接触的各点线速度相同．再正确的选择an＝ω²r或an＝，进行求解.

自我检测

1．关于质点做匀速圆周运动，下列说法正确的是(　　)

A．由an＝知an与r成反比

B．由an＝ω²r知an与r成正比

C．由ω＝知ω与r成反比

D．由ω＝2πn知ω与转速n成正比

解析　由关系式y＝kx知，y与x成正比的前提条件是k为定值．只有当v一定时，才有an与r成反比；只有当ω一定时，才有an与r成正比．

答案　D

2．一小球被细绳拴着，在水平面内做半径为R的匀速圆周运动，向心加速度为a_n，那么(　　)

A．小球运动的角速度ω＝

B．小球在时间t内通过的路程为s＝t

C．小球做匀速圆周运动的周期T＝

D．小球在时间t内可能发生的最大位移为2R

解析　由a_n＝Rω²可得ω＝ ；由a_n＝可得v＝，所以t时间内通过的路程为s＝vt＝t；由a_n＝Rω²＝·R，可知T＝2π；位移由初位置指向末位置的有向线段来描述，对于做圆周运动的小球而言，位移大小即为圆周上两点间的距离，最大值为2R.故正确答案为A、B、D.

答案　ABD

3．关于北京和广州随地球自转的向心加速度，下列说法中正确的是(　　)

A．它们的方向都是沿半径指向地心

B．它们的方向都在平行于赤道的平面内指向地轴

C．北京的向心加速度比广州的向心加速度大

D．北京的向心加速度比广州的向心加速度小

解析　如图所示，地球表面各点的向心加速度方向都在平行于赤道的平面内指向地轴，选项B正确，A错误；设地球半径为R₀，在地面上纬度为φ的P点，做圆周运动的轨道半径r＝R₀cos φ，其向心加速度为an＝ω²r＝ω²R₀cos φ.由于北京的地理纬度比广州的大，cos φ小，两地随地球自转的角速度相同，因此北京随地球自转的向心加速度比广州的小，选项D正确，选项C错误．

答案　BD

4．由于地球自转，比较位于赤道上的物体1与位于北纬60°的物体2，则有(　　)

A．它们的角速度之比ω₁:ω₂＝2:1

B．它们的线速度之比v₁:v₂＝2:1

C．它们的向心加速度之比a₁:a₂＝2:1

D．它们的向心加速度之比a₁:a₂＝4:1

解析　同在地球上，物体1和物体2的角速度必相等，设物体1的轨道半径为R，则物体2的轨道半径为R·cos60°，所以，v₁:v₂＝ωR:ωRcos60°＝2:1，

a₁:a₂＝ω²R:ω²Rcos60°＝2:1.

答案　BC

5．甲乙两球均在水平面上做匀速圆周运动，甲球的轨道半径是乙球轨道半径的2倍，甲球的转速是30 r/min，乙球的转速是15 r/min，则两小球的向心加速度之比为(　　)

A．1∶1    B．2∶1    C．8∶1    D．4∶1

解析　ω＝2πn，an＝ω²r，故＝()²＝8∶1，C项正确．

答案　C

6．一物体以4 m/s的线速度做匀速圆周运动，转动周期为2 s，则物体在运动过程的任意时刻，速度变化率大小为(　　)

A．2 m/s²                                                      B．4 m/s²

C．0                                                             D．4π m/s²

解析　做匀速圆周运动的物体的速度变化率大小即为向心加速度大小，a_n＝ω·v＝·v＝×4 m/s²＝4π m/s².故D选项正确．

答案　D

7．在图中，A、B为咬合传动的两齿轮，R_A＝2R_B，则A、B两轮边缘上两点的关系正确的是(　　)

  

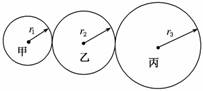
A．角速度之比为2:1

B．向心加速度之比为1:2

C．周期之比为1:2

D．转速之比为2:1

解析　根据两轮边缘线速度大小相等．由v＝rω、ω＝知角速度之比为1:2，A项错误；由a_n＝得向心加速度之比为1:2，B项正确；由T＝得周期之比为2:1，C项错误；由n＝，转速之比为1:2，故D项错误．

答案　B

8．某变速箱中有甲、乙、丙三个齿轮，如图所示，其半径分别为r₁，r₂，r₃，若甲轮的角速度为ω，则丙轮边缘上某点的向心加速度为(　　)

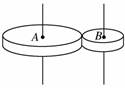
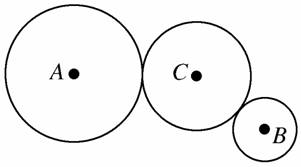
A.                                                           B.

C.                                                           D.

解析　三个齿轮边缘的线速度相等，即v₁＝v₂＝v₃，则有ωr₁＝ω₂r₂＝ω₃r₃，由向心加速度公式a_n＝＝，故选项A正确．

答案　A

9．如图所示，压路机前后轮半径之比是1∶3，A、B分别是前后轮边缘上的点，C为后轮上的一点，它到后轮轴心的距离是后轮半径的一半．则当压路机运动后三点A、B、C的角速度之比为________，向心加速度之比为_______．

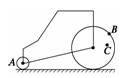
解析　压路机在地面上行驶，不打滑时，两轮边缘的线速度大小相等，这里的地面好像是连接两轮的皮带．

因压路机前后轮在相等时间内都滚过相同的距离，则前、后轮边缘上的A、B线速度大小相等，而同一轮上的B、C点具有相同的角速度．

根据v_A＝v_B，ω_B＝ω_C和v＝ωr

可得ω_A∶ω_B＝∶＝∶＝3∶1

所以ω_A∶ω_B∶ω_C＝3∶1∶1

根据an＝ω²r，可得a_A＝ωr_A，a_B＝ωr_B，a_C＝ωr_C

所以a_A∶a_B∶a_C＝(3ω_C)²r_A∶(ω·3r_A)∶(ω·r_A)＝9∶3∶＝6∶2∶1.

答案　3∶1∶1　6∶2∶1

10．质量相等的A、B两质点分别做匀速圆周运动，若在相等的时间内通过的弧长之比为2:3，而转过的角度之比为3:2，则A、B两质点周期之比T_A:T_B＝__________，向心加速度之比a_A:a_B＝__________.

解析　t相等，故v＝∝s，v_A:v_B＝2:3，

又ω＝∝θ，ω_A:ω_B＝3:2.

T＝∝，∴T_A:T_B＝2:3，

a＝v·ω，∴a_A:a_B＝1:1.

答案　2:3　1:1

11．如图所示，摩擦轮A和B通过中介轮C进行传动，A为主动轮，A的半径为20 cm，B的半径为10 cm，A、B两轮边缘上的点，角速度之比为__________；向心加速度之比为__________．

 

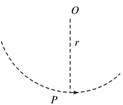
解析　由题知，A、B、C三轮边缘上的点的线速度相等．所以v＝r_Aω_A＝r_Bω_B，故＝＝，又a＝vω∝ω，所以＝.

答案　1:2　1:2

   12．飞机由俯冲转为拉起的一段轨迹可以看成圆弧，如图所示，如果这段圆弧的半径r＝800 m，飞行员承受的加速度为8 g．飞机在最低点P的速率不得超过多少？(g＝10 m/s²)

解析　飞机在最低点做圆周运动，其向心加速度最大不得超过8 g才能保持飞行员安全，由a_n＝得v＝＝ m/s＝80 m/s.

答案　80 m/s