第五章  章末总结

要点归纳

知识点一、曲线运动的合力、轨迹、速度之间的关系

1．轨迹特点：轨迹在速度方向和合力方向之间，且向合力方向一侧弯曲．

2．合力的效果：合力沿切线方向的分力改变速度的大小，沿径向的分力改变速度的方向，如下图所示的两个情景．

(1)当合力方向与速度方向的夹角为锐角时，物体的速率将增大；

(2)当合力方向与速度方向的夹角为钝角时，物体的速率将减小；

(3)当合力方向与速度方向垂直时，物体的速率不变．

知识点二、小船渡河和牵连速度问题的分析

1．小船渡河过程中，随水漂流和划行这两个分运动互不干扰，各自独立而且具有等时性．因此只要分运动时间最短，则合运动时间最短，即船头垂直指向对岸渡河时间最短，t_min＝.航程最短，则要求合位移最小．当v_水<v_船时，合运动的速度可垂直于河岸，最短航程为河宽．当v_水>v_船时，船不能垂直到达河岸，但仍存在最短航程，当v_船与v_合垂直时，航程最短，x_min＝d.

2．跨过定滑轮拉绳(或绳拉物体)运动的速度分解

物体运动的速度为合速度v，物体速度v在沿绳方向的分速度v₁就是使绳子拉长或缩短的速度，物体速度v的另一个分速度v₂就是使绳子摆动的速度，它一定和v₁垂直．

知识点三、抛体运动的规律及应用

1．平抛运动的研究方法及其规律

(1)研究方法：根据运动的合成与分解，可将平抛运动分解为水平方向的匀速直线运动和竖直方向的自由落体运动来进行研究．

(2)平抛运动规律

①

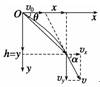
位移：若以初速度v₀水平抛出，以抛出点为坐标原点，水平方向为x轴，竖直方向为y轴，如图所示，则经时间t的位移为

时间t内物体的位移为s＝＝

tan θ＝＝

②速度某点的瞬时速度为v＝＝

tan α＝＝

③平抛运动轨迹是抛物线由(a)(b)两式消去t得y＝x²

④飞行时间由(b)式得t＝ ＝

物体做平抛运动的飞行时间t仅由抛出点的高度h决定，与抛出时的初速度v₀无关．

⑤水平位移x＝v₀t＝v₀

物体做平抛运动的水平位移x由v₀和高度h共同决定．在h一定时，x仅由v₀决定．

⑥速度变化量：Δv＝gΔt.

  

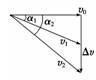
平抛运动的物体在任意一段时间内的速度变化量方向竖直向下，其中v₀、Δv、v三个矢量经过平移可构成直角三角形，如图所示．

⑦平抛运动速度偏向角与位移偏向角的关系

位移偏向角θ：tan θ＝＝

速度偏向角α：tan α＝＝

所以tan α＝2tan θ

2．抛体运动规律的比较

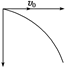
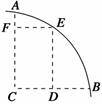
知识点四、利用平抛运动的轨迹解题

       平抛运动的轨迹是一条抛物线，已知抛物线上的任意一段，就可求出水平初速度和抛出点，其他物理量也就迎刃而解了．设图4为某小球做平抛运动的一段轨迹，在轨迹上任取两点A和B，分别过A点作竖直线，过B点作水平线，两直线相交于C点，然后过BC的中点D作垂线交轨迹于E点，过E点再作水平线交AC于F点，则小球经过AE和EB的时间相等，设为单位时间T.

由竖直方向上的匀变速直线运动得FC－AF＝gT²，所以T＝ ＝

由水平方向上的匀速直线运动得v₀＝＝EF

由于小球从抛出点开始在竖直方向上做自由落体运动，在连续相等的时间内满足h₁∶h₂∶h₃∶…＝1∶3∶5∶….因此，只要求出的值，就可以知道AE和EB是在哪个单位时间段内．

典例分析

一、速度的分解

例1 如图所示，在一光滑水平面上放一个物体，人通过细绳跨过高处的定滑轮拉物体，使物体在水平面上运动，人以大小不变的速度v运动．当绳子与水平方向成θ角时，物体前进的瞬时速度是多大？

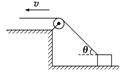
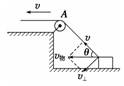
解析　绳子牵引物体的运动中，物体实际在水平面上运动，这个运动就是合运动，

所以物体在水平面上运动的速度v_物是合速度，将v_物按右图所示进行分解．

其中v＝v_物cos θ，使绳子收缩．v_⊥＝v_物sin θ，使绳子绕定滑轮上的A点转动．

所以v_物＝.

答案　

归纳总结：分析绳、杆等有长度的物体，其两端点的速度联系，关键是找准合运动与分运动.

二、平抛运动的规律应用

例2  横截面为直角三角形的两个相同斜面紧靠在一起，固定在水平面上，如图1所示．现有三个小球从左边斜面的顶点以不同的初速度向右平抛，最后落在斜面上．其落点分别是a、b、c.下列判断正确的是(　　)

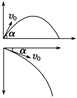
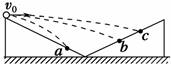
A．图中三小球比较，落在a点的小球飞行时间最短

B．图中三小球比较，落在c点的小球飞行时间最短

C．图中三小球比较，落在c点的小球飞行过程速度变化最大

D．图中三小球比较，落在c点的小球飞行过程速度变化最快

解析　小球在平抛运动过程中，可分解为竖直方向的自由落体运动和水平方向的匀速直线运动，由于竖直方向的位移为落在c点处的最小，而落在a点处的最大，所以落在a点的小球飞行时间最长，落在c点的小球飞行时间最短，A错误、B正确；而速度的变化量Δv＝gt，所以落在c点的小球速度变化最小，C错误；三个小球做平抛运动的加速度都为重力加速度，故三个小球飞行过程中速度变化一样快，D错误．

答案　B

归纳总结：处理平抛运动的基本方法就是化曲为直，要画出运动的示意图，依据平行四边形定则和几何关系求解.

三、类平抛问题的求解

例3  光滑水平面上，一个质量为2 kg的物体从静止开始运动，在前5 s受到一个沿正东方向、大小为4 N的水平恒力作用；从第5 s末开始改为正北方向、大小为2 N的水平恒力作用了10 s，求物体在15 s内的位移和15 s末的速度及方向．

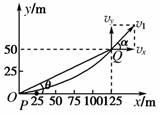
解析：　如右图所示，物体在前5 s内由坐标原点起向东沿x轴正方向做初速度为零的匀加速运动，其加速度为a_x＝＝ m/s²＝2 m/s²方向沿x轴正方向．

5 s末物体沿x轴方向的位移

x₁＝a_xt₁²＝×2×5² m＝25 m，到达P点，5 s末速度v_x＝a_xt₁＝2×5 m/s＝10 m/s.

从第5 s末开始，物体参与两个分运动：一是沿x轴正方向做速度为10 m/s的匀速运动，经10 s其位移x₂＝v_xt₂＝10×10 m＝100 m

二是沿y轴正方向(正北方向)做初速度为零的匀加速直线运动，其加速度为a_y＝＝ m/s²＝1 m/s²

经10 s沿y轴正方向的位移：y＝a_yt₂²＝×1×10² m＝50 m

沿y轴正方向的速度v_y＝a_yt₂＝1×10 m/s＝10 m/s

设15 s末物体到达Q点，则

QO＝＝ m≈135 m，方向为东偏北θ角，满足tan θ＝

15 s末的速度为v₁＝＝ m/s＝10 m/s

tan α＝＝1

∴α＝45°

即方向为东偏北45°角

答案：　135 m　方向为东偏北θ角，满足tan θ＝  10 m/s　方向为东偏北45°

归纳总结：处理类平抛运动时应注意在受力方向上做匀加速运动，在垂直于力的方向上做匀速直线运动，类平抛运动在电场中经常会涉及．