 第2节 运动的合成与分解
第2节 运动的合成与分解
知识点归纳
知识点一、运动的实验探究
1.实验再现:一端封闭长约1 m的玻璃管内注满清水.水中放一个红蜡做的小圆柱体R.将玻璃管口塞紧.
⑴将这个玻璃管倒置(如图所示).可以看到蜡块上升的速度大致不变.即蜡块做匀速运动.
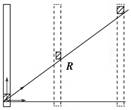
⑵再次将玻璃管上下颠倒.在蜡块上升的同时将玻璃管向右匀速移动,观察研究蜡块的运动.
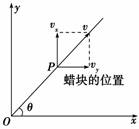
2.实验分析:以开始时蜡块的位置为原点,建立平面直角坐标系,如右图所示.设蜡块匀速上升的速度为vx、玻璃管水平向右移动的速度为vy.从蜡块开始运动的时刻计时,则t时刻蜡块的位置坐标为x=vxt,y=vyt;蜡块的运动轨迹y= x是直线.蜡块位移的大小l=t,位移的方向可以用tanθ=求得.
知识点二、运动的合成与分解
1.平面内的运动:为了更好地研究平面内的物体运动,常建立直角坐标系.
2.合运动和分运动:如果物体同时参与了几个运动,那么物体的实际运动就叫做那几个运动的合运动,那几个运动叫做这个物体实际运动的分运动.
3.运动的合成与分解:由已知分运动求跟它们等效的合运动叫做运动的合成;反之,由已知的合运动求跟它等效的分运动叫做运动的分解,即:

4.运动合成和分解所遵循的法则.
描述运动的物理量(位移、速度、加速度等)都是矢量,对它们进行合成和分解时可运用平行四边形定则和三角形定则.
知识点三、合运动和分运动的关系
1.同一直线上两个分运动的合成.
(1)同一直线上两个分运动的合运动是直线运动;
(2)合运动是匀速还是变速取决于两个分运动,举例来说:
①两个匀速直线运动合成后仍是匀速直线运动;
②一个匀速直线运动和一个匀变速直线运动合成后是匀变速直线运动;
③两个匀变速直线运动的加速度如果等大反向,则其合运动是匀速直线运动.
2.互成角度的两个直线运动的合成
(1)两个匀速直线运动的合运动仍然是匀速直线运动.
(2)一个匀速直线运动和一个匀变速直线运动合成时,由于其加速度与合速度不在同一条直线上,故合运动是匀变速曲线运动.
(3)两个初速度为零的匀加速直线运动的合运动,加速度等于两分运动的加速度a1、a2的矢量和,由于初速度为零,故物体的合运动是沿合加速度的方向做匀加速直线运动.
(4)两个初速度不为零的匀加速直线运动,其初速度v1和v2的矢量和为v,加速度a1和a2的矢量和为a;若v和a在一条直线上,则物体做匀变速直线运动,若v和a不在一条直线上,则物体做匀变速曲线运动.
3.合运动与分运动的关系
(1)等效性:各分运动合成起来与合运动相同,即分运动与合运动可以“等效替代”.
(2)独立性:一个物体同时参与两个分运动,其中的任一分运动并不会因为存在另外的分运动而有所改变.即各分运动是互相独立、互不影响的.
(3)等时性:各个分运动与合运动总是同时开始、同时结束,经历的时间相等.因此知道了某一个分运动的时间,也就知道了合运动的时间,反之也成立.
(4)同体性:合运动和它的分运动必须对应同一个物体的运动,一个物体的合运动不能分解为另一个物体的分运动.
知识点四、小船渡河问题
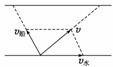
船横渡过河时,船的实际运动v(即相对于河岸的运动)可以看成是随水以速度v水漂流的运动和以速度v船相对于静水的划行运动的合运动.这两个分运动互不干扰而且具有等时性,如图所示.
1.渡河时间t最短问题
(1)渡河时间t的大小取决于河岸的宽度d及船 在垂直河岸方向上的速度的大小.
在垂直河岸方向上的速度的大小.
(2)若要渡河时间最短,只要使船头垂直于河岸航行即可.由图可知,此时tmin=,船渡河的位移x=,位移方向满足tan θ=.
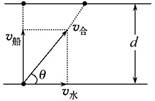
2.渡河位移最短问题
求解渡河位移最短问题,分为两种情况:
(1)若v水<v船,最短的位移为河宽d,此时渡河所用时间t=,船头与上游夹角满足cos θ=,如图所示.
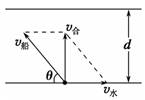
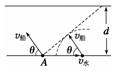
(2)若v水>v船,这时无论船头指向什么方向,都无法使船垂直河岸渡河,即最短位移不可能等于河宽d,寻找最短位移的方法是:如图所示,按水流速度和船的静水速度大小的比例,先从出发点A开始做矢量v水,再以v水末端为圆心,以v船大小为半径画圆弧,自出发点A向圆弧做切线,其方向为船位移最小时的合运动的方向.这时船头与河岸夹角θ满足 cos
θ=,最短位移xmin=,过河时间t=.
cos
θ=,最短位移xmin=,过河时间t=.
典例分析
一、运动的合成与分解
 例1
例1 质量m=2 kg的物体在光滑平面上运动,其分速度vx和vy随时间变化的图象如图中(a)、(b)所示,求:
质量m=2 kg的物体在光滑平面上运动,其分速度vx和vy随时间变化的图象如图中(a)、(b)所示,求:
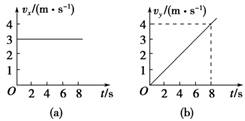
(1)物体的初速度;(2)t=8 s时物体的速度;(3)t=4 s时物体的位移大小.
解析 (1)由题图可知t=0时,vx=3 m/s,vy=0,所以物体的初速度v0=3 m/s,方向沿x轴正方向.
(2)由题图可知t=8 s时,vx=3 m/s,vy=4 m/s,所以v==5 m/s,tan θ=.
所以θ=53°,即速度方向与x轴夹角为53°.
(3)t=4 s时,x=vxt=12 m,y=ayt2=4 m.
物体的位移大小s=≈12.6 m.
答案 (1)3 m/s,方向沿x轴正方向 (2)5 m/s,方向与x轴夹角为53° (3)12.6
m
归纳总结:弄清运动物体的合、分运动,利用平行四边形定则去求解合、分运动的物理量.
二、船渡河问题
 例2
例2 小船在200 m宽的河中横渡,水流速度是2 m/s,小船在静水中的航速是4 m/s.求:(1)要使小船渡河耗时最少,应如何航行?(2)要使小船航程最短,应如何航行?
小船在200 m宽的河中横渡,水流速度是2 m/s,小船在静水中的航速是4 m/s.求:(1)要使小船渡河耗时最少,应如何航行?(2)要使小船航程最短,应如何航行?
解析 (1)如图甲所示,船头始终正对河对岸航行时耗时最少,即最短时间tmin== s=50 s.
(2)如图乙所示,航程最短为河宽d,即应使v合的方向垂直于河对岸,故船头应偏向上游,与河岸成α角,有cos α===,解得α=60°.
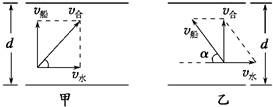
答案 (1)船头正对河岸航行耗时最少,最短时间为50 s.
(2)船头偏向上游,与河岸成60°角,最短航程为200 m.
归纳总结:船过河的实际运动可看作随水漂流v水和相对于静水的划行运动v船的合运动,这两个分运动互不干扰,各自独立,且具有等时性.明确船头正对河岸行驶时,并不到达河的正对岸,而是漂向下游一段距离,要使小船到达河的正对岸,船头应与岸的上游成一角度.
三、绳通过滑轮拉物体的运动问题
 例3
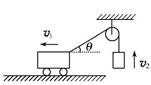
例3 如图所示,水平面上的小车向左运动,系在车后的轻绳绕过定滑轮,拉着质量为m的物体上升。若小车以v1的速度做匀速直线运动,当车后的绳与水平方向的夹角为θ时,物体的速度为v2,绳对物体的拉力为FT,则下列关系式正确的是( )
如图所示,水平面上的小车向左运动,系在车后的轻绳绕过定滑轮,拉着质量为m的物体上升。若小车以v1的速度做匀速直线运动,当车后的绳与水平方向的夹角为θ时,物体的速度为v2,绳对物体的拉力为FT,则下列关系式正确的是( )
A.v2=v1
B.v2=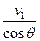
C.FT=mg
D.FT>mg
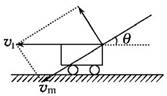
解析 如图所示,将小车的速度v1向垂直轻绳和沿轻绳方向分解,则沿轻绳方向分解的速度vm=v1cosθ,故物体的速度v2=v1cosθ,A、B错误;由于角θ逐渐减小,cosθ变大,故v2逐渐变大,物体加速向上,处于超重状态,FT>mg,C错,D对。
答案 D
归纳总结:分析这类问题,要分清哪个是合运动,哪个是分运动,物体A的实际运动就是合运动.A物体沿绳方向的分速度也即绳子运动的速度,从而找到A物体与人的速度之间的联系.
 自我检测
自我检测
1.对于两个分运动的合运动,下列说法正确的是( )
A.合运动的速度大于两个分运动的速度
B.合运动的速度一定大于某一个分运动的速度
C.合运动的方向就是物体实际运动的方向
D.由两个分速度的大小就可以确定合速度的大小
解析 根据平行四边形定则,合速度的大小和方向可由平行四边形的对角线表示,而两邻边表示两个分速度,由几何关系知,两邻边和对角线的长短关系因两邻边的夹角不同而不同,当两邻边长短不变,而夹角改变时,对角线的长短也将发生改变,即合速度也将变化,故A、B、D错误,C正确.
答案 C
2.已知河水自西向东流动,流速为v1,小船在静水中的速度为v2,且v2>v1,用小箭头表示船头的指向及小船在不同时刻的位置,虚线表示小船过河的路径,则下图中可能正确的是( )

解析 小船的实际速度应该是v1和v2的合速度,根据速度合成的平行四边形定则知只有C、D图有可能正确.
答案 CD
3.如图图甲所示,起重机将货物沿竖直方向匀速吊起,同时又沿横梁水平向右匀加速运动.此时,站在地面上观察,货物运动的轨迹可能是图乙中的( )
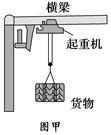
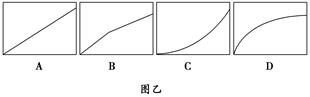
解析 货物同时参与两个方向的运动,一是竖直向上的匀速运动,二是水平向右的匀加速运动,其合运动是曲线运动,运动的加速度水平向右,合外力的方向水平向右,运动轨迹应向合外力方向弯曲,所以站在地面上的人观察到货物的运动轨迹应如D图所示.
答案 D
4.关于运动的合成与分解,下列说法正确的是( )
A.由两个分运动求合运动,合运动是唯一确定的
B.由合运动分解为两个分运动,可以有不同的分解方法
C.物体做曲线运动时,才能将这个运动分解为两个分运动
D.任何形式的运动,都可以用几个分运动代替
解析 根据平行四边形定则,两个分运动的合运动就是以两个分运动为邻边的平行四边形的对角线,A正确.而将合运动分解为两个分运动时,可以在不同方向上分解,从而得到不同的解,B正确.任何形式的运动都可以分解,如竖直上抛运动可以分解成自由落体运动和匀速直线运动的合运动,故C错误,D正确.
答案 ABD
5.如图所示,一名92岁的南非妇女从距地面大约2 700米的飞机上,与跳伞教练绑在一起跳下,成为南非已知的年龄最大的高空跳伞者.假设没有风的时候,落到地面所用的时间为t,而实际上在下落过程中受到了水平方向的风的影响,则实际下落所用时间( )

A.仍为t
B.大于t
C.小于t
D.无法确定
解析 依据合、分运动的独立性、等时性,t不变,A正确.
答案 A
6.一物体在光滑的水平桌面上运动,在相互垂直的x方向和y方向上的分运动速度随时间变化的规律如图所示.关于物体的运动,下列说法正确的是( )
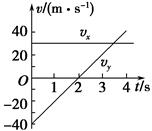
A.物体做曲线运动
B.物体做直线运动
C.物体运动的初速度大小为50 m/s
D.物体运动的初速度大小为10 m/s
解析 由v-t图象可以看出,物体在x方向上做匀速直线运动,在y方向上做匀变速直线运动,故物体做曲线运动,选项A正确,B错误;物体的初速度大小为v0= m/s=50 m/s,选项C正确,D错误.
答案 AC
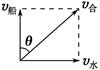
7.小船横渡一条河,船头方向始终与河岸垂直,若小船相对静水的速度大小不变,运动轨迹如图所示,则河水的流速( )
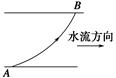
A.由A到B水速一直增大
B.由A到B水速一直减小
C.由A到B水速先增大后减小
D.由A到B水速先减小后增大
解析 由题图可知,合速度的方向与船的速度方向的夹角越来越小,如图所示,由图知v水=v船tan θ,又因为v船不变,故v水一直减小,B正确.
答案 B
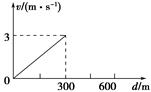
8.某河宽为600 m,河中某点的水流速度v与该点到较近河岸的距离d的关系图象如图所示.船在静水中的速度为4 m/s,要想使船渡河的时间最短,下列说法正确的是( )
A.船在航行过程中,船头应与河岸垂直
B.船在河水中航行的轨迹是一条直线
C.渡河的最短时间为240 s
D.船离开河岸400 m时的速度大小为2 m/s
解析 若船渡河的时间最短,船在航行过程中,必须保证船头始终与河岸垂直,选项A正确;因水流的速度大小发生变化,根据运动的合成与分解可知,船在河水中航行的轨迹是一条曲线,选项B错误;渡河的最短时间为tmin== s=150 s,选项C错误;船离开河岸400 m时的水流速度大小与船离开河岸200 m时的水流速度大小相等,即v水=×200 m/s=2 m/s,则船离开河岸400 m时的速度大小为v′==m/s=2 m/s,选项D正确.
答案 AD
9.某研究性学习小组进行了如下实验:如图所示,在一端封闭的光滑细玻璃管中注满清水,水中放一个红蜡做成的小圆柱体R.将玻璃管的开口端用胶塞塞紧后竖直倒置且与y轴重合,在R从坐标原点以速度v0=3 cm/s匀速上浮的同时,玻璃管沿x轴正方向做初速度为零的匀加速直线运动.同学们测出某时刻R的坐标为(4,6),此时R的速度大小为________cm/s,R在上升过程中运动轨迹的示意图是________.(R视为质点)
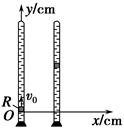
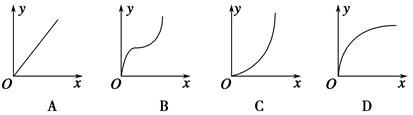
解析 R在竖直方向做匀速直线运动,故运动时间t===2 s;R在水平方向做匀加速直线运动,由平均速度公式可得x=t,解得vx==4 cm/s,故此时R的速度v==5 cm/s.轨迹曲线应弯向加速度的方向,又R的加速度方向沿x轴正方向,故选项D正确.
答案 5 D
10.北风速度4 m/s,大河中的水流正以3 m/s的速度向东流动,船上的乘客看见轮船烟囱冒出的烟柱是竖直的,求轮船相对于水的航行速度多大?什么方向?
解析 本题的研究对象有北风、水流、乘客、烟柱;“烟柱是竖直的”说明烟柱感觉不到风,即人感觉不到风,那么轮船应该与风同速.轮船的实际航向正南,大小为4 m/s.由于河水流动,轮船应该有一个分速度大小与v水相等,方向与v水相反,这样轮船才会朝正南方向行驶,如下图所示.
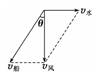
tan θ==,则θ=37°
即船头应该与上游河岸成53°角航行且v船== m/s=5 m/s.
答案 5 m/s 船头与上游河岸成53°角
11.如图所示,河宽d=120 m,设小船在静水中的速度为v1,河水的流速为v2.小船 从A点出发,在渡河时,船身保持平行移动.若出发时船头指向河对岸上游的B点,经过10 min,小船恰好到达河正对岸的C点;若出发时船头指向河正对岸的C点,经过8 min,小船到达C点下游的D点.求:
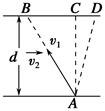
(1)小船在静水中的速度v1的大小;
(2)河水的流速v2的大小;
(3)在第二次渡河中小船被冲向下游的距离sCD.
解析 (1)小船从A点出发,若船头指向河正对岸的C点,则此时渡河时间最短,故有v1== m/s=0.25 m/s.
(2)设AB与河岸上游成α角,由题意可知,此时恰好到达河正对岸的C点,故v1沿河岸方向的分速度大小恰好等于河水的流速v2的大小,即v2=v1cos α,此时渡河时间为t=,所以sin α==0.8故v2=v1cos α=0.15 m/s.
(3)在第二次渡河中小船被冲向下游的距离为sCD=v2tmin=72 m.
答案 (1)0.25 m/s (2)0.15 m/s (3)72 m
(责任编辑:admin)