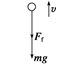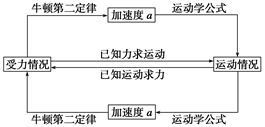
第5节　牛顿定律的应用

知识点归纳

知识点一、利用牛顿运动定律来处理两类基本问题

1．动力学的两类基本问题

(1)已知物体的受力情况，分析确定物体的运动情况．

知道物体的受力情况，用牛顿第二定律求出物体的加速度，再结合物体运动的初始条件，应用运动学公式，可以求出物体的运动情况——任意时刻的位移和速度．

(2)已知物体的运动情况，分析求出物体所受的未知力情况．

知道物体的运动情况，应用运动学公式求出物体的加速度，再应用牛顿定律推断或求出物体受到的合外力，从而得到需求的动力学物理量，如力、质量、动摩擦因数等．

(3)由以上两类问题的分析可知：加速度是由动力学过渡到运动学或由运动学过渡到动力学必经的桥梁．

2．应用牛顿运动定律的基本思路

(1)灵活选取研究对象．

(2)将研究对象提取出来，分析物体的受力情况并画受力示意图，分析物体的运动情况并画运动过程简图．

(3)利用牛顿第二定律或运动学公式求加速度．通常用正交分解法建立直角坐标系，并将有关矢量进行分解，取加速度的方向为正方向，题中各物理量的方向与规定的正方向相同时取正值，反之取负值．

(4)列出方程并求解，检查答案是否完整、合理．

两类问题的解题思路如下：

知识点二、应用牛顿运动定律解题的一般步骤

1．认真分析题意，明确已知条件和所求量．

2．选取研究对象．所选取的研究对象可以是一个物体，也可以是几个物体组成的整体．同一题目，根据题意和解题需要也可以先后选取不同的研究对象．

3．分析研究对象的受力情况和运动情况．

4．当研究对象所受的外力不在一条直线上时：如果物体只受两个力，可以用平行四边形定则求其合力；如果物体受力较多，一般把它们正交分解到两个方向上，分别求合力；如果物体做直线运动，一般把各个力分解到沿运动方向和垂直于运动的方向上．(有时分解加速度)

5．根据牛顿第二定律和运动学公式列方程，物体所受外力、加速度、速度等都可根据规定的正方向按正、负值代入公式，按代数和进行计算．

6．求解方程，检验结果，必要时对结果进行讨论.

知识点三、受力分析

1．受力分析的依据

(1)在受力分析时，只分析根据力的性质命名的力，一般不需要画出“合力”或“分力”的示意图．

(2)每分析一个力，应该可以找出该力的施力物体和该力对物体产生的效果，否则，该力的存在就值得考虑，如不要误认为物体在运动方向上一定受到力的作用．

(3)受力分析时，有时还需结合物体的运动状态．

2．受力分析的方法

(1)明确研究对象，即对谁进行受力分析．

(2)按顺序分析受力情况，画出力的示意图．

知识点四、整体法与隔离法处理连接体问题

1．连接体问题：所谓连接体就是指多个相互关联的物体，它们一般具有相同的运动情况(有相同的速度、加速度)．

2．隔离法与整体法

(1)隔离法：在求解系统内物体间的相互作用力时，从研究的方便性出发，将物体系统中的某部分分隔出来，单独研究的方法．

(2)整体法：整个系统或系统中的几个物体有共同的加速度，且不涉及相互作用时，将其作为一个整体研究的方法．

3．对连接体的一般处理思路

(1)先隔离，后整体．

典例分析

一、由受力情况确定运动情况

例1 在海滨游乐场有一种滑沙的娱乐活动．如图所示，人坐在滑板上从斜坡的高处A点由静止开始下滑，滑到斜坡底部B点后沿水平滑道再滑行一段距离到C点停下来，斜坡滑道与水平滑道间是平滑连接的，滑板与两滑道间的动摩擦因数为μ＝0.50，不计空气阻力，重力加速度g＝10 m/s2.

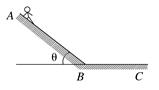
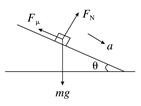
(1)若斜坡倾角θ＝37°，人和滑板的总质量为m＝60 kg，求人在斜坡上下滑时的加速度大小．(sin37°＝0.6，cos37°＝0.8)

(2)若由于受到场地的限制，A点到C点的水平距离为x＝50 m，为确保人身安全，假如你是设计师，你认为在设计斜坡滑道时，对高度应有怎样的要求？

 解析 (1)在斜坡上下滑时，受力如图．由牛顿第二定律得：

mgsinθ－Fμ＝ma　①

FN－mgcosθ＝0　②

Fμ＝μFN　③

解①②③得：a＝gsinθ－μgcosθ＝2 m/s2.

(2)设斜坡倾角为θ，斜坡的最大高度为h，滑至底端时的速度为v，由运动学公式可知：

v²＝2a　④

沿BC段前进时的加速度a′＝μmg/m＝μg　⑤

沿BC段滑行的距离L＝v²/2a′　⑥

为确保安全要求，则L＋≤x　⑦

联立④⑤⑥⑦解得h≤25 m，故斜坡的高度不能超过25 m.

答案　(1)2_m/s2__(2)不能超过25_m

归纳总结：由物体受力情况求解运动情况的一般步骤

(1)确定研究对象，对研究对象进行受力分析，并画出物体受力图．

(2)根据力的合成或正交分解求出合外力(大小、方向)(物体受二个以上的力作用时一般用正交分解法)．

(3)根据牛顿第二定律列方程，并解出物体的加速度．

(4)结合题给物体运动的初始条件，选择运动学公式求出所需的运动学量．

二、由运动情况确定受力情况

例2 将质量为0.5 kg的小球以14 m/s的初速度竖直上抛，运动中球受到的空气阻力大小恒为2.1 N，则球能上升的最大高度是多少？

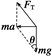
解析　通过对小球受力分析求出其上升的加速度及上升的最大高度．以小球为研究对象，受力分析如图所示．

在应用牛顿第二定律时通常默认合力方向为正方向，题目中求得的加速度为正值，而在运动学公式中

一般默认初速度方向为正方向，因而代入公式时由于加速度方向与初速度方向相反而代入负值．

根据牛顿第二定律得mg＋F_f＝ma，a＝＝ m/s²＝14 m/s²

上升至最大高度时末速度为0，由运动学公式0－v＝2ax

得最大高度x＝＝ m＝7 m.

答案　7 m

归纳总结：1．受力情况决定了运动的性质，物体具体的运动状况由所受合外力决定，同时还与物体运动的初始条件有关．

2．受力情况决定了加速度，但与速度没有任何关系.

三、整体法与隔离法的应用

例3 如图所示，物体A和B的质量分别为1 kg和4 kg，A与墙、A与B之间的动摩擦因数都是0.2，现用F等于150 N的水平力紧压在物体B上，墙面竖直，求A、B间的摩擦力和A、B的运动状态．(g取10 m/s²)

解析　经分析可知，A、B之间无相对滑动，设二者相同的加速度为a，以A、B为一整体，则由牛顿第二定律可得

(m_A＋m_B)g－F_fA＝(m_A＋m_B)a①

又F_fA＝μF②

由①②解得a＝4 m/s²，方向竖直向下．

隔离B，对B有

m_Bg－F_fAB＝m_Ba即F_fAB＝m_B(g－a)＝24 N

即A、B之间的摩擦力为24 N，它们一起以4 m/s²的加速度向下做匀加速直线运动．

答案　见解析

自我检测

1．质量为1 kg的物体，受水平恒力作用，由静止开始在光滑的水平面上做加速运动，它在t秒内的位移为x m。则F的大小为(　　)

A.                                                B.

C.                                           D.

解析 由x＝at²得：a＝ m/s²，对物体由牛顿第二定律得：F＝ma＝1× N＝ N，故A正确。

答案 A

2．用30 N的水平外力F，拉一个静止在光滑水平面上的质量为20 kg的物体，力F作用3 s后消失．则第5 s末物体的速度和加速度分别是(　　)

A．v＝4.5 m/s，a＝1.5 m/s²

B．v＝7.5 m/s，a＝1.5 m/s²

C．v＝4.5 m/s，a＝0

D．v＝7.5 m/s，a＝0

解析　力F作用3 s时速度大小为4.5 m/s，而力F消失后，其速度不再变化，物体加速度为零，故C正确．

答案　C

3．A、B两物体以相同的初速度滑到同一粗糙水平面上，若两物体的质量m_A＞m_B，两物体与粗糙水平面间的动摩擦因数相同，则两物体能滑行的最大距离x_A与x_B相比为(　　)

A．x_A＝x_B　　　　　　　  B．x_A＞x_B

C．x_A＜x_B                         D．不能确定

解析 A、B物体的加速度均为a＝μg，又由x＝知，初速度相同，两物体滑行距离也相同。

答案 A

4．一间新房要盖屋顶，为了使下落的雨滴能够以最短的时间淌离屋顶，则所盖屋顶的顶角应为(设雨滴沿屋顶下淌时，可看作在光滑的斜坡上下滑)(　　)

A．60°  B．90°  C．120°  D．150°

解析　因雨滴沿屋顶的运动过程中仅受重力和支持力作用，设其运动的加速度为a，屋顶的顶角为2α，则由牛顿第二定律易得a＝gcos α.

又因房屋的前后间距已定，设为2b，则雨滴滑动经过的屋顶面长度x＝b/sin α.

由x＝at²得t＝.

显然当α＝45°时对应的时间t最小，即屋顶的顶角应取90°.

答案　B

5．如图所示，小车质量为M，光滑小球P的质量为m，绳质量不计，水平地面光滑，要使小球P随车一起匀加速运动，则施于小车的水平作用力F是(θ已知)(　　)

A．mgtan θ  B．(M＋m)gtan θ

C．(M＋m)gcot θ  D．(M＋m)gsin θ

解析　对小球受力分析如右图所示，则mgtan θ=ma，所以a=gtan θ.对整体F=(M+m)a=(M+m)gtan θ

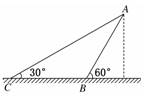
答案　B

6．如图所示为两个等高的光滑斜面AB、AC，将一可视为质点的滑块由静止在A点释放。沿AB斜面运动，运动到B点时所用时间为t_B；沿AC斜面运动，运动到C点所用时间为t_C，则(　　)

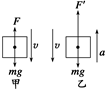
A．t_B＝t_C                          B．t_B>t_C

C．t_B<t_C                            D．无法比较

解析 设斜面倾角为θ，对m利用牛顿第二定律解得加速度a＝g sinθ，解几何三角形得位移x＝，据x＝ at²得t＝ ＝ ＝ ，显然C对。

答案 C

7．质量为60 kg的物体以4 m/s的速度竖直匀速下降，若向上的力突然变为630 N，并持续2 s，则这2 s内物体下落的高度是多少？(g取10 m/s²)

解析　此题属于牛顿运动定律应用的第一类问题，即知道物体的受力情况，求物体的运动情况(运动位移)．

物体做匀速直线运动过程中受两个力的作用，如右图甲所示，F与重力mg是一对平衡力．F=mg=60×10 N=600 N.

当向上的力突然变为F′=630 N时，如图乙所示，由于F′>mg，因此物体的合力方向向上，则由牛顿第二定律可知，物体的加速度必然向上，所以物体将做匀减速直线运动．

选物体为研究对象，取物体运动的方向为正方向，设物体做匀速直线运动的速度为v₀.

物体在减速运动中，合力ΣF=F′-mg，则由牛顿第二定律可得a=0.5 m/s².其方向竖直向上．

物体的初速度方向向下，加速度方向向上，则物体做匀减速直线运动，由运动学公式得

x=v₀t-at²=7 m.

即这2 s内物体下降的高度为7 m.

答案　7 m

8．一辆质量为1.0×10³ kg的汽车，经过10 s由静止加速到速度为108 km/h后匀速前进．求：

(1)汽车受到的合力．

(2)如果关闭汽车发动机油门并刹车，设汽车受到的阻力为6.0×10³ N，求汽车由108 km/h到停下来所用的时间和所通过的路程．

解析　汽车运动过程如下图所示．

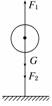
(1)由v=v₀+at得加速度a=3 m/s².由F=ma知汽车受到的合力F=1.0×10³×3 N=3.0×10³ N.

(2)汽车刹车时，由F=ma知 加速度大小a′=6 m/s².

据v=v₀+at知刹车时间t=5 s.

由x=t知 刹车路程x=75 m.

答案　(1)3.0×10³ N　(2)5 s　75 m

9．一个氢气球，质量为200 kg，系一根绳子使它静止不动，且绳子竖直，如图所示。当割断绳子后，气球以2 m/s²的加速度匀加速上升，求割断绳子前绳子的拉力为多大？

解析：以气球为研究对象，绳断前，气球静止，故所受重力G、空气浮 图力F₁、绳的拉力F₂三力平衡：即G＋F₂＝F₁①

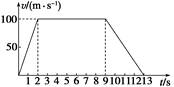
绳断后，气球在空气浮力F₁和重力G的作用下匀加速上升，由牛顿第二定律得：

F₁－G＝ma②

已知a＝2 m/s²所以F₁＝G＋ma＝2400 N，F₂＝F₁－G＝400 N。

答案：400 N

10．在宇航训练程序中，一位80 kg的宇航员被绑在一个质量为220 kg的火箭运载器内，这个运载器被安全放在一条无摩擦的长轨道上，开动火箭发动机使之很快地加速运载器，然后马达制动运载器，v－t图象如图所示．设喷射燃料的质量和运载器的质量比较可以忽略．

(1)计算向前的推力多大；

(2)计算施加在运载器上的制动力；

(3)计算沿导轨运行的路程．

解析　(1)由v－t图知，a＝＝50 m/s²，由F＝(M＋m)a，得F＝1.5×10⁴ N

(2)由v－t图知，9 s～13 s马达制动减速，加速度大小

a′＝＝25 m/s²

则制动力大小F′＝(M＋m)a′＝7.5×10³ N

(3)路程x等于v－t图象与t轴所围面积大小：x＝1 000 m

答案　(1)1.5×10⁴ N　(2)7.5×10³ N　(3)1 000 m