|
【学习目标】 1.知道电势差概念,知道电势差的正负表示两点间电势的高低关系。 2.推导静电力做功跟电势差的关系式,会用公式W1g=qU.g计算静电力所做的功。 3.理解等势面的概念。会画常见电场的等势面。通过论证等势面一定垂直于电场线,体会反证法在推理过程中的应用。 【课前预习】 一、电势差 1.定义:电场中两点间电势的差值叫作电势差,也叫电压。 2.表达式:A、B两点间电势差:UAB=φA-φB ,B、A两点间电势差:UBA=φB-φA ,所以UAB=-UBA。 3.单位:国际单位是伏,符号为V。 4.矢标性:电势差是标量,但有正、负。电势差的正、负表示两点电势的高低。所以电场中各点间的电势差可依次用代数法相加。
5.静电力做功与电势差的关系:
(1)公式推导: WAB=EpA-EpB EpA=qφA EpB=qφB, WAB=qφA-qφB=q(φA-φB)=q·UAB 所以有UAB=。 (2)物理意义:电场中A、B两点间的电势差等于这两点之间移动电荷时静电力做的功与电荷量q的比值。计算两点之间移动电荷十静电力做功,可以不必考虑静电力和电荷移动的路径。
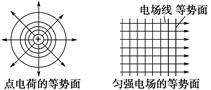
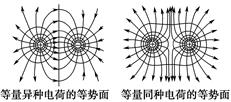
二、等势面 1.定义:电场中电势相同的各点构成的面叫作等势面。 2.特点: (1)电场线跟等势面垂直。(在等势面上任意两点间移动电荷,电场力不做功) (2)电场线由电势高的等势面指向电势低的等势面。 (3)在电场线密集的地方,等势面越密集,电场强度越大。 (4)在空间中两等势面不相交。 (5)等势面是为描述电场的性质而假想的面。
3.几种常见电场的等势面
▲判一判 (1)WAB>0说明电荷从A点移到B点的过程中静电力做正功。 (√) (2)UAB>0说明从A到B电势升高(φA<φB)。 (×) (3)WAB越大,UAB越大,UAB与WAB成正比。 (×) (4)等差等势面的疏密可以表示电场的强弱。 (√) (5)同一电荷在同一等势面上一定具有相同的电势能。 (√) (6)电荷由高等势面移到低等势面,电场力做正功。 (×)
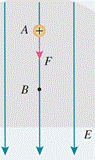
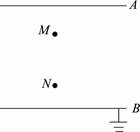
【学习过程】 任务一:对电势差的理解 [例1]如图所示,如果B板接地(取大地的电势为零,则与大地相连的导体的电势也为零), 则A板电势为8 V,M点电势为6 V,N点电势为2 V。 (1)求M、N两点间的电势差是多少伏? (2)如果改为A板接地,问:B点的电势是多大?M、N两点的电势各是多大?M、N两点间的电势差是多少伏?
[解析] (1)M、N两点间的电势差UMN=φM-φN=4 V. (2)若A板接地,则根据UAB=φA-φB,得φB=-UAB=UBA=-8 V M、N两点的电势,φM=UMA=-2 V, φN=UNA=-6 V,UMN=φM-φN=4 V. [变式训练1-1]在电场中A、B两点间电势差为UAB=75 V,B、C两点间电势差UBC=-200 V,则A、B、C三点的电势高低关系为( ) A.φA>φB>φC B.φA<φC<φB C.φC>φA>φB D.φC>φB>φA
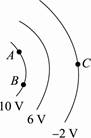
[变式训练1-2] (多选)关于电势差UAB和电势φA、φB的理解,正确的是( ) A.UAB表示B点相对于A点的电势差,即UAB=φB-φA B.UAB和UBA是不同的,它们有关系UAB=-UBA C.φA、φB都可以有正、负,所以电势是矢量 D.电势零点的规定是任意的,但人们通常规定大地或无穷远处为电势零点 [变式训练1-3]如图所示,某电场的等势面用实线表示,各等势面的电势分别为10 V、6 V和-2 V,则UAB=________,UBC=________,UCA=________.
答案:0 12 -12
任务二:电势差与静电力做功关系 [例2]有一带电荷量q=-3×10-6 C的点电荷,从电场中的A点移到B点时,克服静电力做功6×10-4 J,从B点移到C点时,静电力做功9×10-4 J。求: (1)AB、BC、CA间电势差各为多少? (2)如果B点电势为零,则A、C两点的电势各为多少?电荷在A、C两点的电势能各为多少? [解析] (1)根据U= 则UAB= V=200 V 即φA-φB=200 V UBC= V=-300 V 即φB-φC=-300 V UCA=φC-φA=100 V。 (2)若φB=0,则φA=200 V,φC=300 V EpA=φAq=200×(-3×10-6) J=-6×10-4 J EpC=φCq=300×(-3×10-6) J=-9×10-4 J。 [答案] (1)200 V -300 V 100 V (2)200 V 300 V -6×10-4 J -9×10-4 J [变式训练2-1]上例中,若规定A点电势为零,则B、C两点的电势各为多少?电荷在B、C两点的电势能各为多少? 提示:若φA=0,则φB=-200 V,φC=100 V,EpB=φBq=(-200)×(-3×10-6) J=6×10-4 J EpC=φCq=100×(-3×10-6)J=-3×10-4 J。
[变式训练2-2]如图所示,a、b是电场线上的两点,将一点电荷q从a点移到b点,电场力做功W,且已知a、b间的距离为d,以下说法正确的是( )
A.a、b两点间的电势差为 B.b、a两点间的电势差为 C.b点的电势为 D.a点的电势为
[变式训练2-3] (多选)下列关于电势差和静电力做功的说法,正确的是( ) A.电势差的大小由静电力在两点间移动电荷做的功和电荷的电荷量决定 B.静电力在两点间移动某电荷做功的多少由两点间的电势差和该电荷的电荷量决定 C.电势差是矢量,静电力做的功是标量 D.在匀强电场中与电场线垂直的平面上任意两点的电势差均为零 [变式训练2-4] (多选)若在某电场中将5.0×10-8 C的正电荷由A点移到B点,静电力做功6.0×10-3 J,则( ) A.A、B两点间的电势差是1.2×105 V B.A、B两点间的电势差是3.0×10-10 V C.若在A、B两点间由A至B移动2.5×10-8 C的正电荷,则静电力做功3.0×10-3 J D.若在A、B两点间由A至B移动1.0×10-7 C的正电荷,则静电力做功3.0×10-17 J
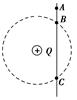
[变式训练2-5] (多选)一个带电小球在从空中a点运动到b点的过程中,重力做功3 J,电场力做功1 J,克服空气阻力做功0.5 J,则小球( ) A.在a点的重力势能比在b点的重力势能大3 J B.在a点的动能比在b点的动能小3.5 J C.在a点的电势能比在b点的电势能小1 J D.在a点的机械能比在b点的机械能小0.5 J [变式训练2-6]如图所示,光滑绝缘的细杆竖直放置,它与以正电荷Q为圆心的某圆交于B、C两点,质量为m、带电荷量为-q的有孔小球从杆上A点无初速度下滑,已知q≪Q,AB=h,小球滑到B点时的速度大小为,其中g为重力加速度,求:
(1)小球由A到B的过程中静电力做的功; (2)A、C两点间的电势差UAC。 思路点拨:(1)点电荷形成的电场中,距离点电荷相等的点电势相等。 (2)电场力做功与路径无关,做功的多少与初末位置的电势差有关。 [解析] (1)因为杆是光滑的,所以小球从A到B的过程中只有两个力做功,即静电力做的功WAB和重力做的功mgh,由动能定理得WAB+mgh=mv 代入已知条件vB=得 WAB=m·3gh-mgh=mgh。 (2)因为B、C在同一等势面上,所以φB=φC 即UAC=UAB==-。 [答案] (1)mgh (2)-
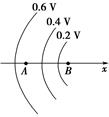
任务三:等势面的理解和应用 [例3] (多选)如图所示,曲线表示一簇关于x轴对称的等势面,在x轴上有A、B两点,则( )
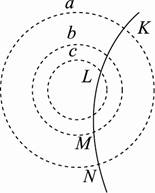
A.A点场强小于B点场强 B.A点场强方向指向x轴负方向 C.A点场强大于B点场强 D.A点电势高于B点电势 [变式训练3-1] (多选)如图所示,虚线同心圆是一簇某静电场中的等势面,其电势分别是φa、φb和φc,一带正电粒子射入电场中,运动轨迹如图中实线KLMN所示.由图可知( )
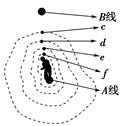
A.粒子从K到L的过程中,静电力做负功,电势能增加 B.粒子从L到M的过程中,静电力做负功,电势能增加 C.φa>φb>φc D.φa<φb<φc [变式训练3-2]在维护和检修高压供电线路时,为了不影响城市用电,电工经常要在高压线上带电作业。为了保障电工的安全,电工全身要穿上用金属丝线编织的衣服。如图所示电工站在高压直流输电线的A供电线上作业,其头顶上方有B供电线,B供电线的电势高于A电线的电势。虚线表示电工周围某一截面上的等势线,c、d、e、f是等势线上的四个点。以下说法正确的是( )
A.在c、d、e、f四点中,c点的电场最强 B.在c、d、e、f四点中,f点的电势最高 C.若将某电子由c移到f,其电势能将增大 D.将某电子在d点由静止释放,它会向e点所在等势面运动
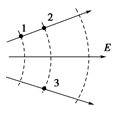
[变式训练3-3]如图所示,实线表示某静电场的电场线,虚线表示该电场的等势面。下列判断正确的是( )
A.1、2两点的电场强度相等 B.1、3两点的电场强度相等 C.1、2两点的电势相等 D.2、3两点的电势相等
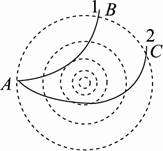
[变式训练3-4]如图所示,图中的虚线表示某电场的等势面,有两个带电粒子(重力不计)以不同的速率,沿不同的方向从A点飞入电场后,沿不同的径迹1和2运动,由轨迹可以判断( ) A.两粒子的电性一定相同 B.粒子1的动能先减小后增大 C.粒子2的电势能先增大后减小 D.经过B、C两点时两粒子的速率可能相等
|