第一章章末总结-同步导学（新教材人教版选择性必修第二册）

第三章章末总结

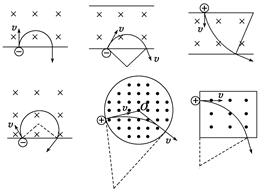
第一章 章末总结

要点归纳

知识点一、通电导线在磁场中的运动及受力

(1)电流元法：即把整段电流等效为多段直线电流元，先用左手定则判断出每小段电流元所受安培力的方向，从而判断出整段电流所受合力的方向，最后确定运动方向．

(2)特殊位置法：把电流或磁铁转到一个便于分析的特殊位置后再判断安培力方向，从而确定运动方向．

(3)等效法：环形电流和通电螺线管都可以等效成条形磁铁，条形磁铁也可等效成环形电流或通电螺线管，通电螺线管也可以等效成很多匝的环形电流来分析．

(4)利用结论法：①两电流相互平行时无转动趋势，同向电流相互吸引，反向电流相互排斥；②两电流不平行时，有转动到相互平行且电流方向相同的趋势，利用这些结论分析，可以事半功倍．

知识点二、带电粒子在有界磁场中的运动

有界匀强磁场指在局部空间存在着匀强磁场，带电粒子从磁场区域外垂直磁场方向射入磁场区域，在磁场区域内经历一段匀速圆周运动，也就是通过一段圆弧后离开磁场区域．由于运动的带电粒子垂直磁场方向，从磁场边界进入磁场的方向不同，或磁场区域边界不同，造成它在磁场中运动的圆弧轨道各不相同．如下面几种常见情景：

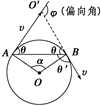
解决这一类问题时，找到粒子在磁场中一段圆弧运动对应的圆心位置、半径大小以及与半径相关的几何关系是解题的关键．

1．三个(圆心、半径、时间)关键确定

研究带电粒子在匀强磁场中做圆周运动时，常考虑的几个问题：

(1)圆心的确定

已知带电粒子在圆周中两点的速度方向时(一般是射入点和射出点)，沿洛伦兹力方向画出两条速度的垂线，这两条垂线相交于一点，该点即为圆心．(弦的垂直平分线过圆心也常用到)

(2)半径的确定

一般应用几何知识来确定．

(3)运动时间：t＝T＝T(θ、φ为圆周运动的圆心角)，另外也可用弧长Δl与速率的比值来表示，即t＝Δl/v.

(4)粒子在磁场中运动的角度关系：

粒子的速度偏向角(φ)等于圆心角(α)，并等于AB弦与切线的夹角(弦切角θ)的2倍，即φ＝α＝2θ＝ωt；相对的弦切角(θ)相等，与相邻的弦切角(θ′)互补，即θ′＋θ＝180°.如图3－2所示．

2．两类典型问题

(1)极值问题：常借助半径R和速度v(或磁场B)之间的约束关系进行动态运动轨迹分析，确定轨迹圆和边界的关系，找出临界点，然后利用数学方法求解极值．

注意　①刚好穿出磁场边界的条件是带电粒子在磁场中运动的轨迹与边界相切．

②当速度v一定时，弧长(或弦长)越长，圆周角越大，则带电粒子在有界磁场中运动的时间越长．

③当速率v变化时，圆周角大的，运动时间长．

(2)多解问题：多解形成的原因一般包含以下几个方面：

①粒子电性不确定；②磁场方向不确定；③临界状态不唯一；④粒子运动的往复性等．

关键点：①审题要细心．②重视粒子运动的情景分析．

要点三 带电粒子在复合场中的运动

复合场是指电场、磁场和重力场并存，或其中某两场并存，或分区域存在的某一空间．粒子经过该空间时可能受到的力有重力、静电力和洛伦兹力．处理带电粒子(带电体)在复合场中运动问题的方法：

①正确分析带电粒子的受力及运动特征是解决问题的前提．

②灵活选用力学规律是解决问题的关键

当带电粒子在复合场中做匀速运动时，应根据平衡条件列方程求解．

当带电粒子在复合场中做匀速圆周运动时，往往同时应用牛顿第二定律和平衡条件列方程联立求解．

当带电粒子在复合场中做非匀速曲线运动时，应选用动能定理或能量守恒定律列方程求解．

典例分析

一、通电导线在磁场中的受力问题

【例1】竖直放置的直导线AB与导电圆环的平面垂直且隔有一小段距离，直导线固定，圆环可以自由运动，当通以如图所示方向的电流时(同时通电)，从左向右看，线圈将(　　)

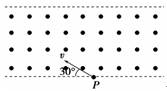
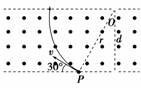
A．顺时针转动，同时靠近直导线AB

B．顺时针转动，同时离开直导线AB

C．逆时针转动，同时靠近直导线AB

D．不动

解析　圆环处在通电直导线的磁场中，由右手螺旋定则判断出通电直导线右侧磁场方向垂直纸面向里，由左手定则判定，水平放置的圆环外侧半圆所受安培力向上，内侧半圆所受安培力方向向下，从左向右看逆时针转，转到与直导线在同一平面内时，由于靠近导线一侧的半圆环电流向上，方向与直导线中电流方向相同，互相吸引，直导线与另一侧半圆环电流反向，相互排斥，但靠近导线的半圆环处磁感应强度B值较大，故F_引>F_斥，对圆环来说合力向左．

答案　C

二、用几何法分析带电粒子在磁场中运动

【例2】　如图所示，在空间中存在垂直纸面向外、宽度为d的有界匀强磁场，一质量为m、带电荷量为q的粒子自下边界的P点处以速度v沿与下边界成30°角的方向垂直射入磁场，恰能垂直于上边界射出，不计粒子重力，题中d、m、q、v均为已知量．则

(1)粒子带何种电荷；

(2)磁场磁感应强度为多少．

解析 (1)粒子从上边界射出，根据左手定则可知粒子带正电．

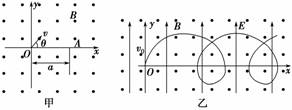
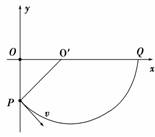
(2)粒子在磁场中的运动轨迹如图所示，设圆周运动半径为r ，由几何关系可得rcos 30°＝d，根据牛顿第二定律有qvB＝m

由以上两式可解得B＝.

答案　(1)正电　(2)

归纳总结：(1)与速度方向垂直的直线和圆上弦的中垂线一定过圆心．

(2)画出粒子运动轨迹，应用勾股定理、三角函数关系等数学方法可确定半径．

(3)找出粒子在磁场中运动对应的圆心角，根据周期公式可求出运动时间．

三、带电粒子在复合场中运动的综合分析

【例3】　如图甲，空间存在一范围足够大的垂直于xOy平面向外的匀强磁场，磁感应强度大小为B.让质量为m，电荷量为q(q>0)的粒子从坐标原点O沿xOy平面以不同的初速度大小和方向入射到该磁场中．不计重力和粒子间的影响．

(1)若粒子以初速度v₁沿y轴正向入射，恰好能经过x轴上的A(a,0)点，求v₁的大小．

(2)已知一粒子的初速度大小为v(v>v₁)，为使该粒子能经过A(a,0)点，其入射角θ(粒子初速度与x轴正向的夹角)有几个？并求出对应的sin θ值．

(3)如图乙，若在此空间再加入沿y轴正向、大小为E的匀强电场，一粒子从O点以初速度v₀沿y轴正向发射．研究表明：粒子在xOy平面内做周期性运动，且在任一时刻，粒子速度的x分量v_x与其所在位置的y坐标成正比，比例系数与场强大小E无关．求该粒子运动过程中的最大速度值v_m.

解析　准确提取题中v_x＝ky的信息，利用带电粒子在匀强磁场中做匀速圆周运动及几何关系、动能定理列式求解．

(1)带电粒子以速率v在匀强磁场B中做匀速圆周运动，半径为R，有qvB＝m①

当粒子沿y轴正向入射，转过半个圆周至A点，该圆周半径为R₁，有：R₁＝②

由②代入①式得v₁＝③

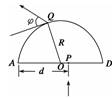
(2)如图，O、A两点处于同一圆周上，且圆心在x＝的直线上，半径为R.

当给定一个初速率v时，有2个入射角，分别在第1、2象限，有sin θ′＝sin θ＝④

由①④式解得sin θ＝

(3)粒子在运动过程中仅电场力做功，因而在轨道的最高点处速率最大，用y_m表示其y坐标，由动能定理，有qEy_m＝mv－mv⑥

由题知，有v_m＝ky_m⑦

若E＝0时，粒子以初速度v₀沿y轴正向入射，有qv₀B＝m⑧

v₀＝kR₀⑨

由⑥⑦⑧⑨式解得v_m＝＋⑩

【答案】　(1)　(2)2个　 (3)＋

归纳总结：这类问题综合了带电粒子在电场和磁场组成的复合场中的匀速直线运动、电场中的类平抛运动、磁场中的匀速圆周运动三个方面．

(1)在电场和磁场组成的复合场中做匀速直线运动时，符合二力平衡，qE＝qvB.

(2)若撤去磁场，带电粒子在电场中做类平抛运动，应用运动的合成与分解的方法分析．

(3)若撤去电场，带电粒子在磁场中做匀速圆周运动，符合洛伦兹力提供向心力：qvB＝m.

四、带电粒子在有界磁场中的运动

【例4】如图所示，在半径为R的半圆形区域中有一匀强磁场，磁场的方向垂直于纸面，磁感应强度为B.一质量为m，带电荷量为q的粒子以一定的速度沿垂直于半圆直径AD方向经P点(AP＝d)射入磁场(不计重力影响)．

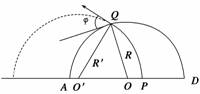
(1)如果粒子恰好从A点射出磁场，求入射粒子的速度．

(2)如果粒子经纸面内Q点从磁场中射出，出射方向与半圆在Q点切线的夹角为φ(如图所示)，求入射粒子的速度．

解析　(1)由于粒子由P点垂直射入磁场，故圆弧轨迹的圆心在AP上，又由粒子从A点射出，故可知AP是圆轨迹的直径．

设入射粒子的速度为v₁，由洛伦兹力的表达式和牛顿第二定律得m＝qv₁B，解得v₁＝.

(2)如下图所示，设O′是粒子在磁场中圆弧轨迹的圆心．连接O′Q，设O′Q＝R′.

由几何关系得∠OQO′=φ

OO′=R′+R-d①

由余弦定理得(OO′)²＝R²＋R′²－2RR′cos φ②

联立①②式得R′＝③

设入射粒子的速度为v，由m＝qvB

解出v＝

答案　(1)　(2)

五、复合场(电场磁场不同时存在)

【例5】在空间存在一个变化的匀强电场和另一个变化的匀强磁场，电场的方向水平向右(如图中由点B到点C)，场强变化规律如图甲所示，磁感应强度变化规律如图乙所示，方向垂直于纸面．从t＝1 s开始，在A点每隔2 s有一个相同的带电粒子(重力不计)沿AB方向(垂直于BC)以速度v₀射出，恰好能击中C点，若AB＝BC＝l，且粒子在点A、C间的运动时间小于1 s，求：

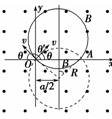
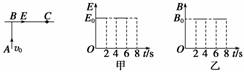
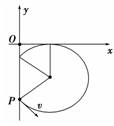
(1)磁场方向(简述判断理由)．

(2)E₀和B₀的比值．

(3)t＝1 s射出的粒子和t＝3 s射出的粒子由A点运动到C点所经历的时间t₁和t₂之比．

解析　(1)由图可知，电场与磁场是交替存在的，即同一时刻不可能同时既有电场，又有磁场．据题意对于同一粒子，从点A到点C，它只受静电力或磁场力中的一种，粒子能在静电力作用下从点A运动到点C，说明受向右的静电力，又因场强方向也向右，故粒子带正电．因为粒子能在磁场力作用下由A点运动到点C，说明它受到向右的磁场力，又因其带正电，根据左手定则可判断出磁场方向垂直于纸面向外．

(2)粒子只在磁场中运动时，它在洛伦兹力作用下做匀速圆周运动．因为AB＝BC＝l，则运动半径R＝l.由牛顿第二定律知：qv₀B₀＝，则B₀＝

粒子只在电场中运动时，它做类平抛运动，在点A到点B方向上，有l＝v₀t

在点B到点C方向上，有a＝，l＝at²

解得E₀＝，则＝

(3)t＝1 s射出的粒子仅受到静电力作用，则粒子由A点运动到C点所经历的时间t₁＝，因E₀＝，则t₁＝，t＝3 s射出的粒子仅受到磁场力作用，则粒子由A点运动到C点所经历的时间t₂＝T，因为T＝，所以t₂＝；故t₁∶t₂＝2∶π.

答案　(1)垂直纸面向外(理由见解析)　(2)2v₀∶1　(3)2∶π

六、巧用临界条件，妙解对称问题

【例6】如图所示，在平面直角坐标系xOy的第四象限有垂直纸面向里的匀强磁场，一质量为m＝5.0×10^－⁸ kg、电量为q＝1.0×10^－⁶ C的带电粒子．从静止开始经U₀＝10V的电压加速后，从P点沿图示方向进入磁场，已知OP＝30 cm，(粒子重力不计，sin 37°＝0.6，cos 37°＝0.8)，求：