第一章  章末总结

要点归纳

知识点一、动量、动能、动量变化量的比较

知识点二、动量定理与动能定理的综合应用

1．两个定理区别：动量定理表示合外力 F 作用积累的冲量，Ft 直接效应是物体动量的变化Δp，是一个矢量规律；动能定理表示合外力作用积累的总功 W，直接效应是物体动能的变化ΔEk，是一个标量规律．动量定理的应用关键是受力分析，确定正方向、明确冲量及初末动量的正负，此正负是表示矢量的方向．动能定理的应用关键是受力分析，明确各力做功的正负，此正负是表示做功的效果不同，是标量的正负．

2．应用动量定理、动能定理解决实际问题，注意解题的一般步骤，思路分析，正确受力分析，运动分析，选择合适的物理过程、物理状态，应用定理列式求解．

(1)动量定理解题的基本思路

①选取研究对象；

②确定所研究的物理过程及其始、末状态；

③分析研究对象所研究的物理过程中的受力情况；

④规定正方向，根据动量定理列方程式；

⑤解方程，统一单位，求解结果．

知识点三、动量守恒定律与机械能守恒定律的综合应用

应用动量守恒定律和机械能守恒定律时，研究对象必定是系统；此外，这些规律都是运用于物理过程，而不是对于某一状态(或时刻)．因此，在用它们解题时，首先应选好研究对象和研究过程．对象和过程的选取直接关系到问题能否解决以及解决起来是否简便．选取时应注意以下几点：

(1)选取研究对象和研究过程，要建立在分析物理过程的基础上，临界状态往往应作为研究过程的开始或结束状态．

(2)要能视情况对研究过程进行恰当的理想化处理．

(3)可以把一些看似分散的、相互独立的物体圈在一起作为一个系统来研究，有时这样做，可使问题大大简化．

(4)有的问题，可以选这部分物体作研究对象，也可以选取那部分物体作研究对象；可以选这个过程作研究过程，也可以选那个过程作研究过程；这时，首选大对象、长过程．

典例分析

一、子弹打击问题

例1 如图所示，质量为M的天车静止在光滑水平轨道上，下面用长为L的细线悬挂着质量为m的沙箱，一颗质量为m₀的子弹以v₀的水平速度射入沙箱，并留在其中，在以后运动过程中，求：

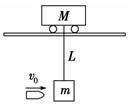
(1)沙箱上升的最大高度；

(2)天车的最大速度。

解析 (1)子弹打入沙箱过程中动量守恒m₀v₀＝(m₀＋m)v₁

摆动过程中，子弹、沙箱、天车系统水平方向动量守恒，机械能守恒。

沙箱到达最大高度时，系统有相同的速度，设为v₂，则有

(m₀＋m)v₁＝(m₀＋m＋M)v₂

(m₀＋m)v＝(m₀＋m＋M)v＋(m₀＋m)gh

联立三式可得沙箱上升的最大高度h＝

(2)子弹和沙箱再摆回最低点时，天车速度最大，设此时天车速度为v₃，沙箱速度为v₄，由动量守恒得(m₀＋m)v₁＝Mv₃＋(m＋m₀)v₄

由系统机械能守恒得(m₀＋m)v＝Mv＋(m＋m₀)v

联立两式可求得天车的最大速度v₃＝v₁＝v₀

答案：(1)　(2)v₀

归纳总结：应用动量的观点、能量的观点解决问题时，比牛顿运动定律更有优越性，那就是不用考虑过程的细节，直接研究初、末状态即可。其实并不是所有的问题都是这样处理的，本题要是直接研究初、末状态就会出错，问题的关键在于本题中含有一个碰撞过程，一般的碰撞过程中都有机械能损失，所以，这个碰撞的细节就一定要拿出来研究。

二、动量定理的综合应用

例2 如图所示，铁块质量 m＝4 kg，以速度v＝2 m/s 水平滑上一静止的平板车，平板车质量 M＝16 kg，铁块与平板车之间的动摩擦因数μ＝0.2，其他摩擦不计(g 取10 m/s2)，求：

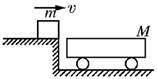
(1)铁块相对平板车静止时，铁块的速度；

(2)铁块在平板车上滑行的最长时间；

(3)铁块在平板车上滑行的最大距离．

解析 铁块滑上平板车后，在车对它的摩擦力的作用下开始减速，车在铁块对它的摩擦力作用下开始加速，当两者速度相等时，铁块相对平板车静止，不再发生相对滑动．

(1)铁块滑上板车的过程中，两者组成的系统动量守恒，取v 的方向为正方向．

则 mv＝(M＋m)v′

v′＝＝0.4 m/s，即铁块相对平板车静止时，铁块速度为0.4 m/s.

(2)以铁块为研究对象，铁块受的摩擦力方向跟铁块速度方向相反，取v方向为正方向．

方法一：由牛顿第二定律：－μmg＝ma　①

由运动学公式知：v′＝v＋at　②

由①②可得：t＝＝0.8 s

方法二：由动量定理：－μmgt＝mv′－mv得：t＝＝0.8 s

本问题也可以取平板车为研究对象进行求解，但应注意，平板车受的摩擦力 F＝μmg，F≠μMg.

(3)方法一：铁块在平板车上滑行时，两者都做匀变速直线运动，且运动时间相同，

因此铁块对地：x₁＝t

平板车对地：x₂＝t

铁块在平板车上滑行的最大距离

Δx＝x₁－x₂＝t－t＝t＝0.8 m

要使铁块在平板车上不滑下，平板车至少长0.8 m.

方法二：由功能关系得μmgΔx＝mv²－(M＋m)v′²

代入数据解之得Δx＝0.8 m.

答案 (1)0.4 m/s   (2)0.8 s    (3)0.8 m

三、动量守恒定律与机械能守恒定律的综合应用

例3 如图所示，位于光滑水平桌面上的小滑块P 和 Q 都可视作质点，质量均为 m，Q 与轻质弹簧相连，设 Q静止，P 以初速度 v0向 Q 运动并与弹簧发生碰撞．求整个碰撞过程中，弹簧具有的最大弹性势能和 Q 的最大动能各为多少？

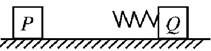
解析 对 P、Q 弹簧组成的系统，水平方向不受外力，水平方向上动量守恒，当 P、Q 速度相等时，动能损失最多，弹性势能最大，这是完全非弹性碰撞模型．

对P、Q弹簧组成的系统，从P开始压弹簧到弹簧被压到最短的过程，由动量守恒定律得mv₀＝2mv　①

由能的转化和守恒定律知ΔE_p＝mv－×2mv²　②

解①②得：ΔE_p＝mv

从P开始压缩弹簧到弹簧恢复原长的整个过程，Q一直加速，所以弹簧刚恢复原长时Q的动能最大，该过程为弹性碰撞模型．

由动量守恒定律知：mv₀＝mv_P＋mv_Q　③

由机械能守恒定律知：mv＝mv＋mv　④

解③④得v_P＝0，v_Q＝v₀

Q的最大动能为E_k＝mv＝mv.

答案 mv　mv

四、多体问题

例4 如图所示，在光滑水平面上有 A、B 两辆小车，水平面的左侧有一竖直墙，在小车 B 上坐着一个小孩，小孩与 B 车的总质量是 A 车质量的 10 倍．两车开始都处于静止状态，小孩把 A 车以相对于地面的速度 v 推出，A 车与墙壁碰后仍以原速率返回，小孩接到 A 车后，又把它以相对于地面的速度 v 推出．每次推出，A 车相对于地面的速度都是 v，方向向左．则小孩把 A 车推出几次后，A 车返回时不能再接到 A 车？

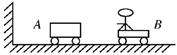
解析 取水平向右为正方向，小孩第一次推出A车时有

m_Bv₁－m_Av＝0即：v₁＝v

第n次推出A车时：m_Av＋m_Bv_n－1＝－m_Av＋m_Bv_n

则：v_n－v_n－1＝v，所以：v_n＝v₁＋(n－1)v

当v_n≥v时，再也接不到小车，由以上各式解得n≥5.5，n取整数，故n＝6.

答案 6 次

五、临界问题

例5 如图所示，滑块A、C质量均为m，滑块B质量为m。开始时A、B分别以v₁、v₂的速度沿光滑水平轨道向固定在右侧的挡板运动；现将C无初速度地放在A上，并与A粘合不再分开，此时A与B相距较近，B与挡板相距足够远。若B与挡板碰撞后以原速率反弹，A与B碰撞将粘合在一起。为使B能与挡板碰撞两次，v₁、v₂应满足什么关系？

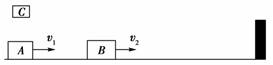
解析 设向右为正方向，A与C粘合在一起的共同速度为v′，

由动量守恒定律得mv₁＝2mv′                                                      ①

为保证B碰挡板前A未能追上B，应满足v′≤v₂                                                       ②

设A与B碰后的共同速度为v″，由动量守恒定律得

2mv′－mv₂＝mv″                                        ③

为使B能与挡板再次碰撞应满足v″>0                                         ④

联立①②③④式得1．5v₂<v₁≤2v₂或v₁≤v₂<v₁                                                     ⑤

答案 1.5v₂<v₁≤2v₂或v₁≤v₂<v₁