|
第5节 弹性碰撞和非弹性碰撞 知识点归纳 知识点一、碰撞 1.碰撞的特点 (1)时间特点:在碰撞现象中,相互作用时间很短. (2)相互作用力的特点:在碰撞过程中物体间的相互作用力先是急剧增大,然后再急剧减小,即相互作用力为变力,作用时间短,作用力很大,且远远大于系统的外力,即使系统所受外力之和不为零,外力也可以忽略,满足动量近似守恒的条件,故均可用动量守恒定律来处理. (3)在碰撞过程中,没有其他形式的能转化为机械能,则系统碰撞后的总机械能不可能大于碰撞前系统的总机械能. (4)位移特点:由于碰撞过程是在一瞬间发生的,时间极短,所以,在物体发生碰撞瞬间,可忽略物体的位移,即认为物体在碰撞、爆炸前后仍在同一位置,但速度发生了突变. 2.碰撞过程应满足的条件 (1)系统的总动量守恒. (2)系统的机械能不增加,即Ek1′+Ek2′≤Ek1+Ek2. (3)符合实际情况,如碰后两者同向运动,应有 v前>v后,若不满足,则该碰撞过程不可能. 3.碰撞与爆炸的异同点
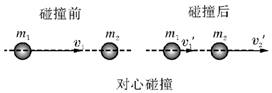
知识点二、对心碰撞和非对心碰撞 1.对心碰撞:如图所示,一个运动的球与一个静止的球碰撞,碰撞之前球的运动速度与两球心的连线在同一条直线上,碰撞之后两球的速度仍会沿着这条直线.这种碰撞称为正碰,也叫对心碰撞.
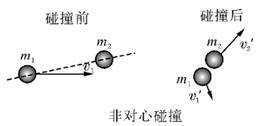
2.非对心碰撞:如图所示,一个运动的球与一个静止的球碰撞,如果碰撞之前球的运动速度与两球心的连线不在同一条直线上,碰撞之后两球的速度都会偏离原来两球心的连线.这种碰撞称为非对心碰撞.
知识点三、弹性碰撞和非弹性碰撞 1.弹性碰撞:如果碰撞过程中机械能守恒,这样的碰撞叫做弹性碰撞,如图所示碰撞中,由动量守恒得 m1v1 =m1v1′+m2v2′,由机械能守恒得m1v=m1v1′2+m2v2′2,解得v1′=v1,v2′=v1.
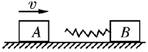
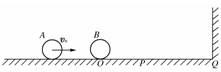
(1)若m1=m2,则有v1′=0,v2′=v1; (2)若m1≫m2,则有v1′=v1,v2′=2v1; (3)若m1≪m2,则有v1′=-v1,v2′=0. 2.非弹性碰撞: (1)如果碰撞过程中机械能不守恒,这样的碰撞叫做非弹性碰撞. (2)若两个物体碰撞时成为一个整体,即它们相对静止,这样的碰撞叫做完全非弹性碰撞,如图所示发生完全非弹性碰撞,则有动量守恒 m1v1=(m1+m2)v;碰撞损失机械能ΔE=v,此时动能损失最大. 知识点四、碰撞中的临界问题 相互作用的两个物体在很多情况下可当做碰撞处理,那么对相互作用中两物体相距恰“最近”、相距恰“最远”或恰上升到“最高点”等一类临界问题,求解的关键都是“速度相等”,相当于完全非弹性碰撞模型.具体分析如下: (1)如图所示,光滑水平面上的 A 物体以速度 v 去撞击静止的 B 物体,A、B 两物体相距最近时,两物体速度必定相等,此时弹簧最短,其压缩量最大.
(2)如图所示,光滑水平面上有两个带同种电荷的物体 A、B,当其中一个 A 以速度 v 向静止的另一个 B 靠近的过程中(设 A、B 不会接触),当两者相距最近时,二者速度必定相等.
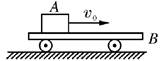
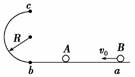
(3)如图所示,物体 A 以速度 v0滑上静止在光滑水平面上的小车 B,当 A 在 B 上滑行的距离最远时,A、B 相对静止,A、B 两物体的速度必定相等.
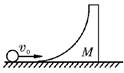
(4)如图所示,质量为 M 的滑块静止在光滑水平面上,滑块的光滑弧面底部与桌面相切,一个质量为 m 的小球以速度 v0 向滑块滚来,设小球不能越过滑块,则小球到达滑块上的最高点时(即小球的竖直速度为零),两物体的速度必定相等(方向为水平向右).
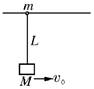
(5)如图所示,光滑水平杆上有一质量为 m 的环,通过一长为 L 的轻绳与 M 相连,现给 M 以瞬时水平速度 v0.(设M 上升最高不超过水平杆),则 M 上升最高时,m、M 速度必定相等.
典例分析 一、动量守恒和能量守恒
(1) 碰后乙的速度的大小; (2) 碰撞中总机械能的损失. 解析 (1)设运动员甲、乙的质量分别为m、M.碰前速度大小分别为v1和v2,碰后乙的速度为v3,由动量守恒定律得:mv1-Mv2=Mv3 代入数据得:v3=1.0 m/s. (2)设碰撞过程中总机械能的损失为ΔE,应有: mv+Mv=Mv+ΔE 答案 (1)1.0 m/s (2)1 400 J 归纳总结:本题考查了动量守恒和能量守恒的综合,难度不大,在运用动量守恒定律解题时,知道动量守恒的表达式是矢量式,需注意速度的方向. 二、对心碰撞
A.甲球速度为零,乙球速度不为零 B.两球速度都不为零 C.乙球速度为零,甲球速度不为零 D.两球都以各自原来的速率反向运动 解析 首先根据两球动能相等,m甲v=m乙v得出两球碰前动量大小之比为:=,因m甲>m乙,则p甲>p乙,则系统的总动量方向向右.根据动量守恒定律可以判断,碰后两球运动情况可能是A、B所述情况,而C、D情况是违背动量守恒的,故C、D情况是不可能的. 答案 AB 三、碰撞中的极值问题
(1)A 物体获得的最大速度; (2)弹簧压缩最大时 B 物体的速度. 解析 (1)对子弹进入A中的过程,由动量守恒定律得:mv0=(m+mA)v1,解得它们的共同速度,即A的最大速度v1==. (2)以子弹及A、B组成的系统作为研究对象,整个作用过程中总动量守恒,弹簧具有最大压缩量时,它们的速度相等,由动量守恒定律得:mv0=(m+mA+mB)v2,解得三者的共同速度,即弹簧有最大压缩量时B物体的速度v2==v0. 答案 (1) (2) 自我检测 1.下列对于碰撞的理解正确的是( ) A.碰撞是指相对运动的物体相遇时,在极短时间内它们的运动状态发生了显著变化的过程 B.在碰撞现象中,一般内力都远远大于外力,所以可以认为碰撞时系统的总动量守恒 C.如果碰撞过程中机械能也守恒,这样的碰撞叫作非弹性碰撞 D.微观粒子的碰撞由于不发生直接接触,所以不满足动量守恒的条件,不能应用动量守恒定律求解 解析 碰撞过程中机械能守恒的碰撞为弹性碰撞,C错.动量守恒定律是自然界普遍适用的规律之一,不仅低速、宏观物体的运动遵守这一规律,而且高速、微观物体的运动也遵守这一规律,D错. 答案 AB 2.现有甲、乙两滑块,质量分别为3m和m,以相同的速率v在光滑水平面上相向运动,发生了碰撞.已知碰撞后,甲滑块静止不动,那么该碰撞是( ) A.弹性碰撞 B.非弹性碰撞 C.完全非弹性碰撞 D.条件不足,无法确定 解析 由动量守恒定律有:3mv+mv=0+mv′,得v′=2v.碰前总动能:Ek=×3mv2+mv2=2mv2,碰后总动能:Ek′=mv′2=2mv2,则Ek′=Ek,选项A正确. 答案 A 3.在两个物体碰撞前后,下列说法中可以成立的是( )
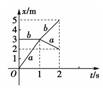
B.作用前后总动量均为零,但总动能守恒 C.作用前后总动能为零,而总动量不为零 D.作用前后总动量守恒,而系统内各物体的动量增量的总和不为零 解析 选项A为非弹性碰撞,成立;选项B为完全非弹性碰撞,成立;总动能为零时,其总动量一定为零,故选项C不成立;总动量守恒,则系统内各物体动量的增量不为零的话,则系统一定受到合外力作用,选项D错误. 答案 AB 4.在光滑水平面上,一质量为m,速度大小为v的A球与质量为2m静止的B球碰撞后,A球的速度方向与碰撞前相反,则碰撞后B球的速度大小可能是( ) A.0.6v B.0.4v C.0.3v D.0.2v 解析 A、B两球在水平方向上合外力为零,A球和B球碰撞的过程中动量守恒,设A、B两球碰撞后的速度分别为v1、v2, 原来的运动方向为正方向,由动量守恒定律有:mv=mv1+2mv2① 假设碰后A球静止,即v1=0,可得v2=0.5v 由题意知球A被反弹,所以球B的速度有v2>0.5v② AB两球碰撞过程能量可能有损失,由能量关系有:mv2≥mv+mv③ ①③两式联立得:v2≤v④ 由②④两式可得:0.5v<v2≤v,符合条件的只有0.6v, 所以选项A正确,B、C、D错误. 答案 A 5.质量为ma=1kg,mb=2kg的小球在光滑的水平面上发生碰撞,碰撞前后两球的位移—时间图象如图所示,则可知碰撞属于( )
A.弹性碰撞 B.非弹性碰撞 C.完全非弹性碰撞 D.条件不足,不能确定 解析 由x-t图象知,碰撞前va=3m/s,vb=0,碰撞后va′=-1m/s,vb′=2m/s,碰撞前动能mav+mbv=J,碰撞后动能mava′2+mbvb′2=J,故机械能守恒;碰撞前动量mava+mbvb=3kg·m/s,碰撞后动量mava′+mbvb′=3kg·m/s,故动量守恒,所以碰撞属于弹性碰撞。 答案 A 6.如图所示,设质量为M的导弹运动到空中最高点时速度为v0,突然炸成两块,质量为m的一块以速度v沿v0的方向飞去,则另一块的运动( )
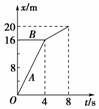
A.一定沿v0的方向飞去 B.一定沿v0的反方向飞去 C.可能做自由落体运动 D.以上说法都不对 解析 根据动量守恒得v′=。mv可能大于、小于或等于Mv0,所以v′可能小于、大于或等于零。 答案 C 7.现有甲、乙两滑块,质量分别为3m和m,以相同的速率v在光滑水平面上相向运动,发生了碰撞。已知碰撞后,甲滑块静止不动,那么这次碰撞是( ) A.弹性碰撞 B.非弹性碰撞 C.完全非弹性碰撞 D.条件不足,无法确定 解析 由动量守恒3m·v-mv=0+mv′,所以v′=2v 碰前总动能:Ek=·3m·v2+mv2=2mv2 碰后总动能:Ek′=mv′2=2mv2, Ek=Ek′,所以A对。 答案 A 8.A、B两物体发生正碰,碰撞前后物体A、B都在同一直线上运动,其位移—时间图象如图所示.由图可知,物体A、B的质量之比为( )
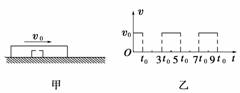
A.1∶1 B.1∶2 C.1∶3 D.3∶1 解析 由图象知,碰撞前vA=4 m/s,vB=0,碰撞后vA′=vB′=1 m/s,由动量守恒定律可知mAvA+0=mAvA′+mBvB′,解得mB=3mA,选项C正确. 答案 C 9.在光滑水平面上,动能为E0、动量为p0的小钢球1与静止小钢球2发生碰撞,碰撞前后球1的运动方向相反,将碰撞后球1的动能和动量大小分别记为E1、p1,球2 的动能和动量的大小分别记为E2、p2,则必有( ) A.E1<E0 B.p1<p0 C.E2>E0 D.p2>p0 解析 两个钢球组成的系统在碰撞过程中动量守恒,设钢球1初动量的方向为正方向,又由动量守恒定律得:p0=p2-p1,可见p2>p0,故选项D正确。单从动量方面分析,p1可以大于p0,若如此必有碰后系统的动能增加,但对于碰撞问题碰撞后系统的动能不可能大于碰前系统的动能,因此E1+E2≤E0,必有E1<E0,E2<E0,显然选项A正确, 选项C错误。由动量的大小和动能的关系p=,因为E1<E0,得p1<p0,选项B正确。 答案 ABD 10.一个物体静置于光滑水平面上,外面扣一质量为M的盒子,如图甲所示。现给盒子一初速度v0,此后,盒子运动的v-t图象呈周期性变化,如图乙所示,请据此求盒内物体的质量。
解析 设物体的质量为m,t0时刻受盒子碰撞获得速度v,根据动量守恒定律得:Mv0=mv ① 3t0时刻物体与盒子右壁碰撞使盒子速度又变为v0,说明物体速度变为零,且碰撞是弹性碰撞,由机械能守恒有:Mv=mv2 ② 联立①②解得m=M 答案 M 11.在光滑的水平面上,质量为m1的小球A以速率v0向右运动,在小球A的前方O点有一质量为m2的小球B处于静止状态,如图所示,小球A与小球B发生正碰后小球A、B均向右运动,小球B被Q处的墙壁弹回后与小球A在P点相遇,PQ=1.5PO,假设小球间的碰撞及小球与墙壁之间的碰撞都是弹性的,求两小球质量之比m1/m2。
解析 从两小球碰撞后到它们再次相遇,小球A和B的速度大小保持不变,根据它们通过的路程,可知小球B和小球A在碰撞后的速度大小之比为4:1。 设碰撞后小球A和B的速度分别为v1和v2,在碰撞过程中动量守恒,碰撞前后动能相等。 m1v0=m1v1+m2v2,m1v=m1v+m2v 利用v2/v1=4,可解出=2 答案 =2 12.如图所示,abc是光滑的轨道,其中ab是水平的,bc为与ab相切的位于竖直平面内的半圆,半径R=0.3 m.质量m=0.20 kg的小球A静止在轨道上,另一质量M=0.60 kg、速度为v0=5.5 m/s的小球B与小球A正碰.已知相碰后小球A经过半圆的最高点c落到轨道上距b点为L=4处,重力加速度g=10 m/s2,求:碰撞结束时,小球A和B的速度的大小.
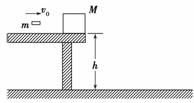
解析 A球平抛,则:水平方向:L=vct;竖直方向:2R=gt2, A球从b点到c点由机械能守恒知:mv+2mgR=mv, A、B碰撞过程由动量守恒:Mv0=mvA+MvB, 由以上各式带入数据解得碰撞结束时,小球A、B速的度分别为:vA=6 m/s, vB=3.5 m/s. 答案 3.5 m/s 13.如图所示,一质量为M的物块静止在桌面边缘,桌面离水平地面的高度为h.一质量为m的子弹以水平速度v0射入物块后,以水平速度射出.重力加速度为g.求:
(1)子弹穿过物块后物块的速度v1; (2)此过程中系统损失的机械能; (3)此后物块落地点离桌面边缘的水平距离. 解析 (1)设子弹穿过物块后物块的速度为v1,由动量守恒得: mv0=m+Mv1① 解得:v1=v0② ( ΔE=mv-③ 由②③式得ΔE=mv④ (3)设物块下落到地面所需时间为t,落地点距桌面边缘的水平距离为s,则: h=gt2⑤; s=v1t⑥ 解得:s=⑦ 答案 (1)v1=v0 (2)ΔE=mv (3)s=
|
|||||||||||||||||||||