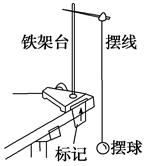
第5节　实验：用单摆测量重力加速度

知识点归纳

知识点：用单摆测定重力加速度

1．实验原理：由T＝2π知g＝.

2．实验器材：带孔小钢球一个，细线一条(约1 m长)、铁架台、毫米刻度尺、秒表、游标卡尺(也可不用)．

3．实验步骤

(1)做单摆

①让线的一端穿过小球的小孔，然后打一个比小孔大一些的结．

②把线的上端用铁夹固定在铁架台上，并把铁架台放在实验桌边，使铁夹伸到桌面以外，让摆球自由下垂，在单摆平衡位置处做上标记，如图所示．

(2)测摆长：用毫米刻度尺量出悬线长l′，精确到毫米；用游标卡尺测量出摆球的直径D，精确到毫米，则l＝l′＋，即为单摆的摆长．

(3)测周期：将单摆从平衡位置拉开一个小于5°角度，然后释放摆球，当单摆摆动稳定后，过平衡位置时用秒表开始计时，测量30～50次全振动的时间．计算出平均摆动一次的时间，即为单摆的振动周期T.

(4)变摆长：将单摆的摆长变短(或变长)，重复实验三次，测出相应的摆长l和周期T.

4．数据处理

(1)平均值法：每改变一次摆长，将相应的l和T，代入公式g＝中求出g值，最后求出g的平均值．

设计如下表所示实验表格

(2)图象法：由T＝2π得T²＝l作出T²­l图象，即以T²为纵轴，以l为横轴．如图所示，其斜率k＝，由图象的斜率即可求出重力加速度g.

5．注意事项

(1)摆线要选1 m左右，不要过长或过短，太长测量不方便，太短摆动太快，不易计数．

(2)摆长要悬挂好摆球后再测，不要先测摆长再系小球，因为悬挂摆球后细绳会发生形变．

(3)计算摆长时要将摆线长加上摆球半径，不要把摆线长当作摆长．

(4)摆球要选体积小、密度大的，不要选体积大、密度小的，这样可以减小空气阻力的影响．

(5)摆角要小于5°(具体实验时可以小于15°)，不要过大，因为摆角过大，单摆的振动不再是简谐运动，公式T＝2π就不再适用．

(6)单摆要在竖直平面内摆动，不要使之成为圆锥摆．

(7)要从平衡位置计时，不要从摆球到达最高点时开始计时．

(8)要准确记好摆动次数，不要多记或少记．

6．误差分析

(1)本实验系统误差主要来源于单摆模型本身是否符合要求，即悬点是否固定；球、线是否符合要求；振动是圆锥摆还是同一竖直平面内的振动以及测量哪段长度作为摆长等等．

(2)本实验偶然误差主要来自时间(即单摆周期)的测量上．要从摆球通过平衡位置开始计时，并采用倒数计时计数的方法，不能多记或漏记振动次数．为了减小偶然误差，进行多次测量后取平均值．

(3)本实验中在长度(摆线长、摆球的直径)的测量时，读数读到毫米即可(即使用游标卡尺测摆球直径也只需读到毫米)；在时间的测量中，秒表读数的有效数字的末位在秒的十分位即可．

典例分析

用单摆测定重力加速度

例 (1)物理课外小组研究“用单摆测重力加速度”实验，他们依照教材实验直接测量的物理量应为________、________、________，其公式为________。

(2)他们测出不同的摆长(l)所对应的周期(T)，在进行数据处理时：①如果甲同学以摆长(l)为横坐标、周期(T)的二次方为纵坐标作出了T²－l图象，若他测得的图象的斜率为k，则测得的重力加速度g＝________。若甲同学测摆长时，忘记测摆球的半径，则他用图象法求得的重力加速度________(选填“偏小”“偏大”或“准确”)。

②乙同学根据公式：T＝2π得出g＝，并计算重力加速度，若乙同学测摆长时，也忘记了测摆球的半径，则他测得的重力加速度________(选填“偏小”“偏大”或“准确”)。

(3)甲同学测量5种不同摆长下单摆的振动周期，记录结果如表所示。

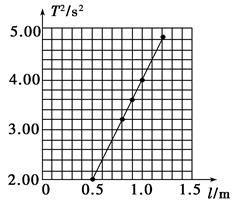
以摆长(l)为横坐标、周期(T)的二次方为纵坐标，作出T²－l图象，请你替他在虚线框中作出T²－l图象，利用此图象求出的重力加速度为________。

解析　(1)本实验是利用单摆的周期公式T＝2π得出g＝，即只要测出摆长l和周期T就能求出当地的重力加速度g，而l＝l₀＋，T＝。显然，本实验直接测量的物理量应为摆线长l₀、摆球直径d以及完成n次全振动所用的时间t。其公式为g＝。

(3)建立如图坐标系，并标出适当的标度，依据数学描点法画出T²－l图象如图所示，则图象的斜率大约为k＝4.0。依据图象求出重力加速度为g＝≈9.86 m/s²。

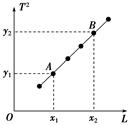
答案　(1)摆线长l₀　摆球直径d　n次全振动的时间  t　g＝　

(2)①　准确　②偏小　(3)T²－l　图象见解析　9.86 m/s²

自我检测

1．在“用单摆测重力加速度”的实验中，若测得的g值比当地的标准值偏小，可能因为(　　)

A．测摆长时摆线拉的过紧

B．测摆长时用摆线长代替摆长而漏加小球半径

C．测量周期时，将n次全振动误记成n＋1次全振动

D．开始记时时，小球通过平衡位置时秒表按下的时刻滞后于小球通过平衡位置的时刻

解析　根据T＝2π，g＝推理得B对．

答案  B

2．在利用单摆测定重力加速度的实验中：

(1)实验中，需要用到绳子、球、计时器以及尺子等，下列给出了一些选择，你认为相对合适的器材是________．(填写序号)

A．1米长细线                                 B．1米长粗线

C．10厘米细线                               D．泡沫塑料小球

E．小铁球  F．秒表

G．时钟  H．厘米刻度米尺

I．毫米刻度米尺

(2)实验中，测出不同摆长L对应的周期值T，作出T²­L图象，如图所示，T²与L的关系式是T²＝________，利用图线上任两点A，B的坐标(x₁，y₁)、(x₂，y₂)可求出图线斜率k，再由k可求出g＝________.

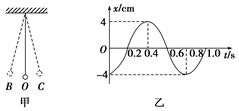
(3)根据(2)中的方法进行实验，若测得的g值偏小，可能是下列原因中的________．

A．计算摆长时，只考虑悬线长度，而未加小球半径

B．测量周期时，将n次全振动误记为n＋1次全振动

C．计算摆长时，将悬线长加小球直径

D．测量周期时，将n次全振动误记为n－1次全振动

解析  (1)为了减少实验误差，摆线选择1米左右的长细线，摆球选择质量大一些，体积小一些的铁球，测量时间用秒表，测量摆长用毫米刻度尺，选择AEFI.

(2)根据单摆的周期公式T＝2π，解得T²＝.

对此图象可知，斜率k＝.

解得g＝.

(3)根据(2)中的求解方法，摆长的测量不影响T²­L图象的斜率，即摆长测量偏大或偏小，g值不变，A、C选项错误；测量周期时，将n次全振动误记为n＋1次全振动，则周期测量值偏小，导致重力加速度测量值偏大，B选项错误；测量周期时，将n次全振动误记为n－1次全振动，则周期测量值偏大，导致重力加速度测量值偏小，D选项正确．

答案  (1)AEFI　(2)　　(3)D

3．(1)在用单摆测定重力加速度的实验中，应选用的器材有________。

A．1 m长的细线                                   B．1 m长的粗线

C．10 cm长的细线                                D．泡沫塑料小球

E．小铁球                                             F.秒刻度秒表

G．时钟                                                 H．厘米刻度尺

I．毫米刻度尺

(2)在该实验中，单摆的摆角θ应________，从摆球经过________开始计时，测出n次全振动的时间为t，用毫米刻度尺测出摆线长为L，用游标卡尺测出摆球的直径为d。用上述物理量的符号写出测定重力加速度的一般表达式为g＝________。

解析　(1)做摆长的细线要用不易伸长的轻线，一般应不短于1米，选A；小球应是密度较大、直径较小的金属球，选E；计时仪器宜选用秒表F；测摆长应选用毫米刻度尺I。

(2)根据单摆做简谐运动的条件知θ≤5°；因平衡位置易判断，且经平衡位置时速度大，用时少，误差小，所以从平衡位置开始计时。

根据T＝2π

又T＝，l＝L＋

得g＝。

答案　(1)A、E、F、I　(2)不大于5°　平衡位置　

4．如图甲所示是一个单摆振动的情形，O是它的平衡位置，B、C是摆球所能到达的最远位置，设向右为正方向，图乙是这个单摆的振动图象，根据图象回答：

(1)单摆振动的频率是多大？

(2)开始时刻摆球在何位置？

(3)若当地的重力加速度为10 m/s²，试求这个单摆的摆长约为多少？(计算结果保留2位小数)

解析　(1)由题图乙知周期T＝0.8 s，

则频率f＝＝1.25 Hz。

(2)由题图乙知，开始时刻摆球在负向最大位移处，因向右为正方向，所以在B点。

(3)由T＝2π得l＝≈0.16 m。

答案　(1)1.25 Hz　(2)B点　(3)0.16 m