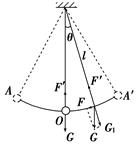
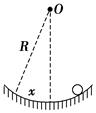
第4节 单摆知识点归纳 知识点一 单摆及单摆的回复力 1.单摆 (1)如果细线的质量与小球相比可以忽略,球的直径与线的长度相比也可以忽略,这样的装置就叫做单摆。单摆是实际摆的理想化模型。 (2)单摆的平衡位置:摆球静止时所在的位置。 2.单摆的回复力 (1)回复力的来源:如图所示,摆球的重力沿圆弧切向的分力提供回复力。
(2)回复力的特点:在偏角很小时,sinθ≈,所以单摆的回复力为F=-x,即小球所受的回复力与它偏离平衡位置的位移成正比,方向总是指向平衡位置,单摆的运动可看成是简谐运动。 3.单摆的运动特点 (1)摆线以悬点为圆心做变速圆周运动,因此在运动过程中只要速度v≠0,半径方向都受向心力. (2)摆线同时以平衡位置为中心做往复运动,因此在运动过程中只要不在平衡位置,轨迹的切线方向都受回复力. 知识点二 单摆的周期 1.伽利略发现了单摆运动的等时性,惠更斯得出了单摆的周期公式并发明了摆钟。 2.单摆的周期 (1)单摆的周期T=2π,只与摆长l及单摆所在处的重力加速度有关,与振幅及摆球的质量无关。单摆的周期叫固有周期。 (2)单摆的周期公式在单摆偏角很小 时成立(偏角为5°时,由周期公式算出的周期和精确值相差0.01%)。 (3)单摆周期公式中的g应为单摆所在处的重力加速度,l应为单摆的摆长。摆长是指从悬点到摆球重心的长度,l=l′+,l′为摆线长,d为摆球直径。 知识点三 单摆的“等效思维”
典例分析 单摆的规律
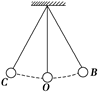
A.单摆运动的回复力是重力和摆线拉力的合力 B.单摆运动的回复力是重力沿圆弧切线方向的一个分力 C.单摆经过平衡位置时合力为零 D.单摆运动的回复力是摆线拉力的一个分力 解析 单摆运动是在一段圆弧上运动,因此单摆运动过程不仅有回复力,而且有向心力,即单摆运动的合外力不仅要提供回复力,还要提供向心力,单摆的回复力是重力沿圆弧切线方向的分力,故选项B正确,A、D错误;单摆经过平衡位置时,回复力为零,向心力最大,故其合力不为零,所以选项C错误. 答案 B 归纳总结:关于单摆的回复力的两点提醒 (1)单摆振动中的回复力不是它受到的合力,而是重力沿圆弧切线方向的一个分力.单摆振动过程中,“摆线拉力”与“重力沿摆线方向的分力”的合力提供向心力,这是与弹簧振子的不同之处. (2)在最大位移处时,因速度为零,所以向心力为零,故此时合力等于回复力. 自我检测 1.关于单摆,下列说法正确的是( ) A.摆球运动的回复力是摆线张力和重力的合力 B.摆球经过轨迹上的同一点速度是相同的 C.摆球经过轨迹上的同一点加速度是相同的 D.摆球经过平衡位置时受力是平衡的 解析 摆球运动的回复力由重力沿圆弧切线方向的分力提供,A错.根据简谐运动的特性可知摆球经过轨迹上的同一点时速度大小相等,方向可能相同,也可能不同,加速度的大小、方向都相同,故B错,C对.摆球经过平衡位置时,回复力为零,合外力不为零,并不平衡,所以D错. 答案 C 2.如图所示是一个单摆(θ<5°),其周期为T
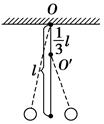
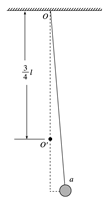
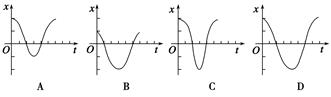
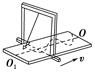
A.把摆球的质量增加一倍,其周期不变 B.摆球的振幅变小时,周期也变小 C.此摆由O →B运动的时间为 D.摆球由B→O时,动能向势能转化 解析 单摆的周期与摆球的质量无关,A正确;单摆的周期与振幅无关,B错误;此摆由O →B运动的时间为,C正确;摆球由B→O时,势能转化为动能,D错误. 答案 AC 3.如图,长为l的细绳下方悬挂一小球a,绳的另一端固定在天花板上O点处,在O点正下方l的O′处有一固定细铁钉.将小球向右拉开,使细绳与竖直方向成一小角度(约为2°)后由静止释放,并从释放时开始计时.当小球a摆至最低位置时,细绳会受到铁钉的阻挡.设小球相对于其平衡位置的水平位移为x,向右为正.下列图象中,能描述小球在开始一个周期内的xt关系的是( )
解析 由单摆的周期公式T=2π可知,小球在钉子右侧时,振动周期为在左侧时振动周期的2倍,所以B、D项错误;由机械能守恒定律可知,小球在左、右最大位移处距离最低点的高度相同,但由于摆长不同,所以小球在左、右两侧摆动时相对平衡位置的最大水平位移不同,当小球在右侧摆动时,最大水平位移较大,故A项正确. 答案 A 4.一个单摆的摆球运动到最大位移时,正好遇到空中竖直下落的雨滴(雨滴质量远小于摆球质量),雨滴均匀附着在摆球的表面,则下列说法正确的是( ) A.摆球经过平衡位置时速度要增大,周期也增大,振幅也增大 B.摆球经过平衡位置时速度没有变化,周期减小,振幅也减小 C.摆球经过平衡位置时速度没有变化,周期也不变,振幅要增大 D.摆球经过平衡位置时速度要增大,周期不变,振幅要增大 解析 在最大位移处,雨滴落到摆球上,质量增大,同时摆球获得初速度,故摆球经过平衡位置时速度增大,单摆的振幅增大,由于雨滴质量远小于摆球质量,摆球仍做简谐运动,由于摆球质量及振幅不影响周期,则周期不变,故选项D正确. 答案 D 5.如图所示为演示简谐运动的沙摆,已知摆长为l,沙桶的质量为m,沙子的质量为M,M>m,沙子逐渐下漏的过程中,沙摆的周期( )
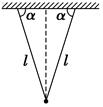
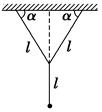
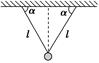
A.不变 B.先变大后变小 C.先变小后变大 D.逐渐变大 解析 在沙摆摆动、沙子逐渐下漏的过程中,沙摆的重心逐渐下降,则等效摆长逐渐变大,当沙子流到一定程度后,沙摆的重心又重新上移,则等效摆长变小,由周期公式可知,沙摆的周期先变大后变小,故选B. 答案 B 6.如图所示,在两根等长的细线下悬挂一个小球(体积可忽略),组成了所谓的双线摆,若细线长均为l,两线与天花板的夹角均为α,当小球垂直纸面做简谐运动时,周期为( )
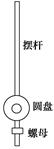
A.2π B.2π C.2π D.2π 解析 这是一个变形的单摆,可以用单摆的周期公式T=2π计算,但注意此处的l与题中的细线长不同,公式中的l是指质点到悬点(等效悬点)的距离,此题中单摆的等效摆长为lsin α,代入周期公式,可得T=2π ,故选D. 答案 D 7.惠更斯利用摆的等时性发明了带摆的计时器,叫摆钟,摆钟运行时克服摩擦所需的能量由重锤的势能提供,运行的速率由钟摆控制.旋转钟摆下端的螺母可以使摆上的圆盘沿摆杆上下移动,如图所示.以下说法正确的是( )
A.当摆钟不准确时需要调整圆盘的位置 B.摆钟快了应使圆盘沿摆杆上移 C.由冬季变为夏季时应使圆盘沿摆杆上移 D.把摆钟从福建移到北京应使圆盘沿摆杆上移 解析 根据周期公式T=2π知,当摆钟不准确时需要调整摆长,A正确;摆钟快了,周期小,则需将摆长增大,增大周期,B错误;由冬季变为夏季时摆杆受热伸长,则需上移圆盘,C正确;摆钟从福建移到北京,重力加速度增大,则需将摆长增大,D错误. 答案 AC |