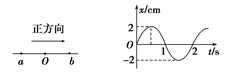|
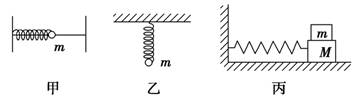
第3节 简谐运动的回复力和能量 知识点归纳 知识点一、简谐运动的回复力 1.简谐运动的动力学定义:如果质点所受的力与它偏离平衡位置位移的大小成正比,并且总是指向平衡位置,质点的运动就是简谐运动。 2.回复力:由于力的方向总是指向平衡位置,它的作用总是要把物体拉回到平衡位置,所以通常把这个力称为回复力。 3.弹簧振子的回复力与位移的关系:F=-kx,式中k是弹簧的劲度系数。 4.回复力的性质:回复力是根据力的效果命名的,它可以是一个力,也可以是多个力的合力,还可以由某个力的分力提供.如图甲所示,水平方向的弹簧振子,弹力充当回复力;如图乙所示,竖直方向的弹簧振子,弹力和重力的合力充当回复力;如图丙所示,m随M一起振动,m的回复力是静摩擦力.
5.简谐运动的回复力的特点 (1)由F=-kx知,简谐运动的回复力大小与振子的位移大小成正比,回复力的方向与位移的方向相反,即回复力的方向总是指向平衡位置. (2)公式F=-kx中的k指的是回复力与位移的比例系数,而不一定是弹簧的劲度系数,系数k由振动系统自身决定. (3)根据牛顿第二定律得,a==-x,表明弹簧振子做简谐运动时振子的加速度大小也与位移大小成正比,加速度方向与位移方向相反. 知识点二、简谐运动的能量 1.能量转化:弹簧振子运动的过程就是动能和势能互相转化的过程。 (1)在最大位移处,势能最大,动能为零。(2)在平衡位置处,动能最大,势能最小。 2.能量特点:在简谐运动中,振动系统的机械能守恒,而在实际运动中都有一定的能量损耗,因此简谐运动是一种理想化的模型。 3.简谐运动的特点: 如图所示的弹簧振子.
说明:简谐运动的位移、回复力、加速度、速度都随时间做周期性变化(正弦或余弦函数),变化周期为T,振子的动能、势能也做周期性变化,周期为T/2。 (1)凡离开平衡位置的过程,v、Ek均减小,x、F、a、EP均增大;凡向平衡位置移动时,v、Ek均增大, x、F、a、EP均减小. (2)在平衡位置时,x、F、a为零,EP最小,v、Ek最大;在最大位移时,x、F、a、EP最大,v、Ek最为零; (3)在平衡位置两侧的对称点上,x、F、a、v、Ek、EP的大小均相同. (4)在简谐运动中,位移、回复力、加速度和势能四个物理量同时增大或减小,与速度和动能的变化步调相反. (5)平衡位置是位移、加速度和回复力方向变化的转折点. (6)最大位移处是速度方向变化的转折点. (7)简谐运动的位移与前面学过的位移不同,简谐运动的位移是从平衡位置指向某一位置的有向线段,位移起点是平衡位置,是矢量. 4.因x=Asin(ωt+φ),故回复力F=-kx=-kAsin(ωt+φ),可见回复力随时间按正弦规律变化。 5.表达式中k虽然是系数,但有单位,其单位是由F和x的单位决定的,即为N/m。 6.简谐运动中,x变化,回复力F随之改变,可见a=也是随x在改变,所以简谐运动是一个变加速运动。其位移跟加速度的关系为a=-x,加速度大小跟位移大小成正比,方向相反。 典例分析 一、简谐振动
(1)小球在振动过程中的回复力实际上是________; (2)该小球的振动是否为简谐运动? 解析 (1)此振动过程的回复力实际上是弹簧的弹力与重力的合力. (2)设振子的平衡位置为O,向下方向为正方向,此时弹簧已经有了一个伸长量h,设弹簧的劲度系数为k,由平衡条件得kh=mg① 当振子向下偏离平衡位置的距离为x时,回复力即合外力为F回=mg-k(x+h) ② 将①代入②式得:F回=-kx,可见小球所受合外力与它的位移的关系符合简谐运动的受力特点,该振动系统的振动是简谐运动. 答案 (1)弹力和重力的合力 (2)是简谐运动 归纳总结:判断是否为简谐运动的方法 (1)以平衡位置为原点,沿运动方向建立直线坐标系. (2)在振动过程中任选一个位置(平衡位置除外),对振动物体进行受力分析. (3)将力在振动方向上分解,求出振动方向上的合力. (4)判定振动方向上合外力(或加速度)与位移关系是否符合F=-kx(或a=-x),若符合,则为简谐运动,否则不是简谐运动. 二、振动图像
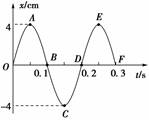
(1)哪些时刻振子有最大动能? (2)哪些时刻振子有相同速度? (3)哪些时刻振子有最大势能? (4)哪些时刻振子有相同的最大加速度? 解析 由题图知,B、D、F时刻振子在平衡位置,具有最大动能,此时振子的速率最大;A、C、E时刻振子在最大位移处,具有最大势能,此时振子的速度为0.B、F时刻振子向负方向运动,D时刻振子向正方向运动,可知D时刻与B、F时刻虽然速率相同,但方向相反.A、E两时刻振子的位移相同,C时刻振子的位移虽然大小与A、E两时刻相同,但方向相反.由回复力知识可知C时刻与A、E时刻振子受力大小相等,但方向相反,故加速度大小相等,方向相反. 答案 (1)B、D、F时刻振子有最大动能 (2)A、C、E时刻振子速度相同,B、F时刻振子速度相同 (3)A、C、E时刻振子有最大势能 (4)A、E时刻振子有相同的最大加速度 归纳总结:对简谐运动能量的三点认识 (1)决定因素:对于一个确定的振动系统,简谐运动的能量由振幅决定,振幅越大,系统的能量越大. (2)能量获得:系统开始振动的能量是通过外力做功由其他形式的能转化来的. (3)能量转化:当振动系统自由振动后,如果不考虑阻力作用,系统只发生动能和势能的相互转化,机械能守恒. 自我检测 1.关于简谐运动,下列说法正确的是( ) A.位移的方向总指向平衡位置 B.加速度方向总和位移方向相反 C.位移方向总和速度方向相反 D.速度方向总跟位移方向相同 解析 简谐运动的位移的初始位置是平衡位置,所以简谐运动过程中任一时刻的位移都是背离平衡位置的,故A选项错误;振子的加速度总是指向平衡位置的,而位移总是背离平衡位置的,故B选项正确;振子在平衡位置两侧往复运动,故C、D选项错误. 答案 B 2.做简谐运动的物体每次经过同一位置时,都具有相同的( ) A.加速度 B.动能 C.位移 D.速度
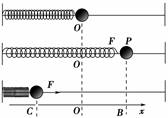
答案 ABC 3.做简谐运动的弹簧振子在某段时间内速度越来越大,则这段时间内( ) A.振子的位移越来越大 B.振子正向平衡位置运动 C.振子速度与位移同向 D.振子速度与位移方向相反 解析 因振子速度越来越大,可判定振子正向平衡位置运动,而位移总是背离平衡位置的,因此速度与位移方向相反,所以选项A、C错误,选项B、D正确. 答案 BD 4.在图中,当振子由A向O运动时,下列说法中正确的是
A.振子的位移在减小 B.振子的运动方向向左 C.振子的位移方向向左 D.振子的位移在增大 解析 对简谐运动而言,其位移总是相对平衡位置O而言,所以C、D错误;由于振子在O点右侧由A向O运动,所以振子的位移方向向右,位移大小不断减小,故A、B正确。 答案 AB 5.关于机械振动的位移和平衡位置,以下说法中正确的是 A.做机械振动的物体必有一个平衡位置 B.机械振动的位移总是以平衡位置为起点的位移 C.机械振动的物体运动的路程越大,发生的位移也越大 D.机械振动的位移是指振动物体偏离平衡位置最远时的位移 解析 物体在平衡位置附近的往复运动叫作机械振动,故A正确;机械振动的位移是以平衡位置为起点指向质点所在位置的有向线段,位移随时间而变,振子偏离平衡位置最远时,振动物体的位移最大,B正确,C、D错误。 答案 AB 6.弹簧振子在光滑水平面上做简谐运动,在振子向平衡位置运动的过程中( ) A.振子所受的力逐渐增大 B.振子的位移逐渐增大 C.振子的速度逐渐减小 D.振子的加速度逐渐减小 解析 根据弹簧振子做简谐运动的特点可知,在振子向平衡位置移动的过程中,位移逐渐减小,所受的力逐渐减小,A、B错误;振子速度逐渐变大,C错误;振子的加速度逐渐减小,D正确. 答案 D 7.如图所示为某简谐运动的图象,若t=0时,质点正经过O点向b点运动,则下列说法正确的是( )
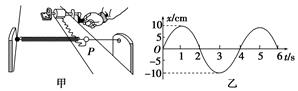
A.质点在0.7 s时,正在远离平衡位置运动 B.质点在1.5 s时的位移最大 C.1.2 s到1.4 s,质点的位移在增大 D.1.6 s到1.8 s,质点的位移在增大 解析 由于位移是由平衡位置指向质点所在位置的有向线段,故质点在0.7 s时的位移方向为正,且正在向平衡位置运动,所以A项错误;质点在1.5 s时的位移最大,故B正确;质点在1.2 s到1.4 s时间内,正在远离平衡位置运动,所以其位移在增加,故C正确;1.6 s到1.8 s时间内,质点正向平衡位置运动,所以其位置在减小,故D项错误。 答案 BC 8.如图甲所示,在弹簧振子的小球上安装一记录用的铅笔P,在下面放一条白纸带,当小球振动时沿垂直于振动方向匀速拉动纸带,铅笔P就在纸带上画出一条振动曲线。若振动曲线如图乙所示,由图象判断下列说法正确的是
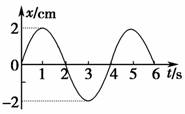
A.振子偏离平衡位置的最大距离为10 cm B.1 s末到5 s末振子的路程为10 cm C.2 s末和4 s末振子的位移相等,运动方向也相同 D.振子在2 s内完成一次往复性运动 解析 由题图图象可知振子偏离平衡位置的最大距离为10 cm,4 s内完成一次往复性运动,A正确,D错误;1 s末到5 s末振子的路程是振子运动路径的总长为40 cm,故B错误;2 s末和4 s末振子位移均为零,位移相同,2 s末振子向负方向运动,4 s末振子向正方向运动,运动方向相反,故C错误。 答案 A 9.弹簧振子做简谐运动,其位移x与时间t的关系如图所示,则( )
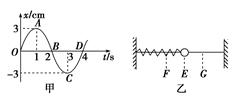
A.在t=1 s时,速度的值最大,方向为负,加速度为零 B.在t=2 s时,速度的值最大,方向为负,加速度为零 C.在t=3 s时,速度的值最大,方向为正,加速度最大 D.在t=4 s时,速度的值最大,方向为正,加速度为零 解析 当t=1 s和t=5 s时,位移最大,加速度最大,速度为零,选项A错误;当t=2 s时,位移为零,加速度为零,而速度最大,速度方向要看该点切线斜率的正负,t=2 s时,速度为负值,选项B正确;当t=3 s时,位移最大,加速度最大,速度为零,选项C错误;当t=4 s时,位移为零,加速度为零,速度最大,方向为正,选项D正确.] 答案 BD 10.图甲为一弹簧振子的振动图象,规定向右的方向为正方向,图乙为弹簧振子的示意图,弹簧振子在F、G之间运动,E是振动的平衡位置,试根据图象分析以下问题:
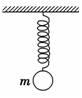
(1)如图乙所示,振子振动的起始位置是________(选填“E”“F”或“G”),从初始位置开始,振子向________(选填“左”或“右”)运动。 (2)在图乙中,找出图象中的A、B、C、D点各对应振动过程中的哪个位置?A对应________,B对应________,C对应________,D对应________。 (3)在t=2 s时,振子的速度方向与t=0时速度方向________(选填“相同”或“相反”)。 (4)振子在前4 s内的位移等于________。 解析 (1)由x-t图象知,在t=0时,振子在平衡位置,故起始位置为E;从t=0时刻开始,振子向正方向运动,即向右运动。 (2)由x-t图象知:B点、D点对应平衡位置E点,A点在正的最大位移处,对应G点;C点在负的最大位移处,对应F点。 (3)t=2 s时,图线斜率为负,即速度方向为负方向;t=0时,斜率为正,速度方向为正方向。故两时刻速度方向相反。 (4)4 s末振子回到平衡位置,故位移为零。 答案 (1)E 右 (2)G E F E (3)相反 (4)0 11.如图所示,一轻质弹簧上端系于天花板上,一端挂一质量为m的小球,弹簧的劲度系数为k,将小球从弹簧为自由长度时的竖直位置放手后,小球做简谐运动,则:
(1)小球从放手运动到最低点,下降的高度为多少? (2)小球运动到最低点时的加速度大小为多少? 解析 (1)放手后小球到达平衡位置时,弹簧伸长了x,则mg=kx,x=,x也是振动过程中球离平衡位置的最大距离,所以小球从放手运动到最低点,下降高度为2x,即。 (2)小球在最高点时只受重力,其加速度为g,最低点和最高点对平衡位置的位移大小相等,故加速度大小相等为g。 答案 (1) (2)g |