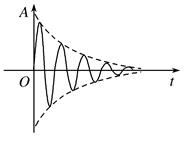
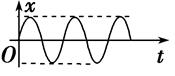
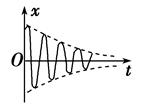
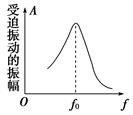
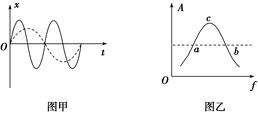
第6节 受迫振动 共振

知识点归纳

知识点一、固有振动

1．固有振动：振动系统不受外力的作用．如：弹簧振子和单摆．

2．固有频率：固有振动的频率．固有频率由振动系统本身因素决定．

知识点二、阻尼振动

1．阻尼振动：振动系统受到阻力的作用，振幅逐渐减小的振动．

2．阻尼振动特点：振幅减小，频率不变(如图)．

3．理想化处理：当阻尼很小时，在短时间内看不出振幅明显减小，可以把它当作简谐运动来处理．

知识点三、受迫振动

1．驱动力：如果存在阻尼作用，振动系统最终会停止振动．为了使系统持续振动下去，对振动系统施加的周期性的外力，外力对系统做功，补偿系统的能量损耗，这种周期性的外力叫做驱动力．

2．受迫振动：在周期性驱动力作用下的振动．

3．受迫振动频率：受迫振动的频率等于驱动力的频率，与系统的固有频率无关．

知识点四、简谐运动、阻尼振动与受迫振动的比较

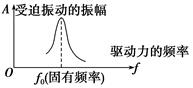
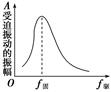
知识点五、共振

1．定义：驱动力的频率f等于系统的固有频率f₀时，受迫振动的振幅最大，这种现象叫做共振。

2．共振曲线(如图所示)

3．发生共振的条件及理解

(1)驱动力的频率等于振动系统的固有频率。

(2)对共振条件的理解：

①从受力角度看：当振动物体所受驱动力的方向跟它的运动方向相同时，驱动力对它起加速作用，使它的振幅增大，当驱动力的频率等于物体的固有频率时，它的每一次作用都使物体的振幅增加，从而振幅达到最大。

②从功能关系看：当驱动力的频率等于物体的固有频率时，驱动力始终对物体做正功，使振动能量不断增加，振幅不断增大，直到增加的能量等于克服阻尼作用损耗的能量，振幅才不再增加。

4．共振曲线及理解

(1)如图所示，当驱动力的频率与物体的固有频率相等时，受迫振动的振幅最大。

(2)对共振曲线的理解

共振曲线直观地反映了物体做受迫振动的振幅与驱动力频率的关系。当驱动力的频率f偏离固有频率f₀较大时，受迫振动的振幅较小；当驱动力的频率，等于固有频率f₀时，受迫振动的振幅最大。

5．共振的应用与防止

(1)共振的应用

①特点：在应用共振时，应使驱动力频率接近或等于振动系统的固有频率，振动将更剧烈．

②实例：转速计、共振筛.

(2)共振的防止

①特点：在防止共振时，驱动力频率与系统的固有频率相差越大越好．

②实例：部队过桥时用　便步；火车过桥时减速；轮船航行时，改变航向或航速．目的都是使驱动力的频率远离物体的固有频率．

典例分析

一、阻尼振动

例1  一单摆在空气中振动，振幅逐渐减小．下列说法正确的是(　　)

A．机械能逐渐转化为其他形式的能

B．后一时刻的动能一定小于前一时刻的动能

C．后一时刻的势能一定小于前一时刻的势能

D．后一时刻的机械能一定小于前一时刻的机械能

E．后一时刻的动能可能大于前一时刻的动能

解析  单摆振动过程中，因不断克服空气阻力做功，使机械能逐渐转化为内能，选项A、D对；虽然单摆总的机械能在逐渐减小，但在振动过程中动能和势能仍不断地相互转化，动能转化为势能时，动能逐渐减小，势能逐渐增大，而势能转化为动能时，势能逐渐减小，动能逐渐增大，所以不能断言后一时刻的动能(或势能)一定小于前一时刻的动能(或势能)，故选项B、C不对，选项E对．

答案  ADE

归纳总结：阻尼振动的能量和周期

(1)阻尼振动的振幅不断减小，能量不断减少，但阻尼振动的频率不变，其频率为固有频率，由系统本身决定．

(2)自由振动是一种理想情况，也叫简谐运动．实际中的振动都会受到阻力的作用，当阻力较小时，可认为是简谐运动．

(3)阻尼振动中，机械能E等于动能E_k和势能E_p之和，即E＝E_k＋E_p，E减小，但动能和势能相互转化，当E_p相等，E_k不相等，而从振动图象上可以确定E_p的关系．

二、受迫振动

例2  如图所示，在曲轴A上悬挂一个弹簧振子，如果转动把手，曲轴可以带动弹簧振子上下振动．问：

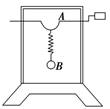
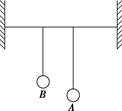
(1)开始时不转动把手，而用手往下拉振子，然后放手让振子上下振动，测得振子在10 s内完成20次全振动，振子做什么振动？其固有周期和固有频率各是多少？若考虑摩擦和空气阻力，振子做什么振动？

(2)在振子正常振动过程中，以转速4 r/s匀速转动把手，振子的振动稳定后，振子做什么运动？其周期是多少？

解析　(1)用手往下拉振子使振子获得一定能量，放手后，振子因所受回复力与位移成正比，方向与位移方向相反(F＝－kx)，所以做简谐运动，其周期和频率是由它本身的结构性质决定的，称固有周期(T_固)和固有频率(f_固)，根据题意T_固＝＝ s＝0.5 s，f_固＝＝ Hz＝2 Hz.由于摩擦和空气阻力的存在，振子克服摩擦力和阻力做功消耗能量，使其振幅越来越小，故振动为阻尼振动．

(2)由于把手转动的转速为4 r/s，它给弹簧振子的驱动力频率为f_驱＝4 Hz，周期T_驱＝0.25 s，故振子做受迫振动．振动达稳定状态后，其频率(或周期)等于驱动力的频率(或周期)，而跟固有频率(或周期)无关．即f＝f_驱＝4 Hz，T＝T_驱＝0.25 s．又因为振子做受迫振动得到驱动力对它做的功，补偿了振子克服阻力做功所消耗的能量，所以振子的振动属于受迫振动．

答案　(1)简谐运动　0.5 s　2 Hz　阻尼振动   (2)受迫振动　0.25 s

归纳总结：1．分析受迫振动的方法

(1)在分析受迫振动时，首先要弄清驱动力的来源．

(2)受迫振动的频率等于驱动力的频率，与物体的固有频率无关，因而首先应确定驱动力的频率．

(3)当驱动力的频率等于固有频率时，发生共振．

2．改变受迫振动的振幅的方法

当f_驱＝f_固时，振幅最大．若改变受迫振动的振幅，可采取两种方法：

(1)改变给予振动系统周期性外力的周期，即改变驱动力频率．

(2)了解影响固有频率的因素，改变固有频率．

自我检测

1．下列各种振动中，不是受迫振动的是(　　)

A．敲击后的锣面的振动

B．缝纫机针的振动

C．人挑担子时，担子上下振动

D．蜻蜓、蝴蝶翅膀的振动

解析  受迫振动是物体在周期性驱动力作用下的运动，而锣面在敲击后并没有受到周期性驱动力作用，A不是受迫振动；B、C、D都在做受迫振动．

答案  A

2．下列说法正确的是(　　)

A．挑水时为了防止水从桶中荡出，可以加快或减慢走路的步频

B．在连续均匀的海浪冲击下，停在海面的小船上下振动，是共振现象

C．部队要便步通过桥梁，是为了防止桥梁发生共振而坍塌

D．较弱声音可震碎玻璃杯，是因为玻璃杯发生了共振

解析  挑水时为了防止水从桶中荡出，可以改变走路的步频，A正确；在连续均匀的海浪冲击下，停在海面的小船上下振动，是受迫振动，B错误；部队便步通过桥梁，不能产生较强的驱动力，就避免桥梁发生共振现象，故C正确；当声音频率等于玻璃杯频率时，杯子发生共振而破碎，D正确．

答案  ACD

3．若空气阻力不可忽略，单摆在偏角很小时，总是减小的物理量为(　　)

A．振幅　　　　　　　　                     B．位移

C．周期                                                 D．机械能

解析  有空气阻力时，振动为阻尼振动，振幅不断减小，机械能不断减小，故A、D正确．平衡位置处的位移为零，则位移不是一直减小，周期T＝2π不变，故B、C错误．

答案  AD

4．弹簧振子在振动过程中振幅逐渐减小，这是由于(　　)

A．振子开始振动时振幅太小

B．在振动过程中要不断克服外界阻力做功，消耗能量

C．动能和势能相互转化

D．振子的机械能逐渐转化为内能

解析  由于阻力作用，振子的机械能减少，振幅减小．故B、D正确．

答案  BD

5．有甲、乙、丙三个单摆，它们的固有频率分别为f、4f、6f，都在频率为4f的驱动力作用下做受迫振动，比较这三个单摆，则(　　)

A．乙的振幅最大，丙的其次，甲的最小

B．乙的振幅最大，甲的其次，丙的最小

C．它们的振动频率都为4f

D．乙的振动频率为4f，甲的振动频率为f，丙的振动频率为6f

解析  驱动力的频率为4f，与乙摆的固有频率相同，因此乙发生共振，所以乙的振幅最大；丙的固有频率为6f，甲的固有频率为f，所以丙的固有频率更接近驱动力的频率，所以丙的振幅大于甲的振幅，但比乙小，故A正确，B错误；由于三个单摆均做受迫振动，因此其频率均为4f，故C正确，D错误．

答案  AC

6．如图所示，两个质量分别为M和m的小球A、B，悬挂在同一根水平细线上，当A在垂直于水平细线的平面内摆动时，不计空气阻力，经过足够长的时间，下列说法正确的是(　　)

A．两摆的振动周期是相同的

B．当两摆的摆长相等时，B摆的振幅最大

C．悬挂A的竖直细线长度变化时，B摆的振幅一定减小

D．无论怎样改变悬挂A的竖直细线长度，B摆的振幅都不变

解析　A摆动时，B摆做受迫振动，稳定后，B摆的振动周期应等于驱动力的周期，即等于A摆的周期，选项A正确；当B摆长与A摆长相等时，两者的固有周期相等，而A摆的固有周期就是使B做受迫振动的驱动力的周期，可见B摆处于共振状态，B摆的振幅最大，选项B正确；A摆长发生变化，就是使B做受迫振动的驱动力周期发生变化，由于B的固有周期不变，这样两个周期差别就发生了变化，因而B的振幅也要发生变化但不一定减小，选项C、D错误．

答案  AB

7．铺设铁轨时，每两根钢轨接缝处都必须留有一定的间隙，匀速运行的列车经过轨端接缝处时，车轮就会受到一次冲击．由于每一根钢轨长度相等，所以这个冲击力是周期性的，列车受到周期性的冲击做受迫振动．普通钢轨长为12.6 m，列车固有振动周期为0.315 s．下列说法正确的是(　　)

A．列车的危险速率为40 m/s

B．列车过桥需要减速，是为了防止列车发生共振现象

C．列车运行的振动频率和列车的固有频率总是相等的

D．增加钢轨的长度有利于列车高速运行

解析　当列车受到冲击的频率和列车故有频率相同时，会发生共振，比较危险，由T＝可得危险车速为v＝＝ m/s＝40 m/s，A正确；列车过桥需要减速，是为了防止桥与列车发生共振现象，B错误；列车的速度不同，则振动频率不同，C错误；由题意可知，根据T＝可知增加长度可以使危险车速增大，故可以使列车高速运行，D正确．

答案  AD

8．下表记录了某振动系统的振幅随驱动力频率变化的关系，若该振动系统的固有频率为f_固，则(　　)

A．f_固＝60 Hz                                  B．60 Hz<f_固<70 Hz

C．50 Hz<f_固<60 Hz                         D．40 Hz<f_固<50 Hz

解析　如图所示的共振曲线，可判断出f_驱与f_固相差越大，受迫振动的振幅越小，f_驱与f_固越接近，受迫振动的振幅越大，并从中看出f_驱越接近f_固，振幅的变化越慢，比较各组数据知f_驱在50～60 Hz范围内时振幅变化最小，因此50 Hz<f_固<60 Hz，C正确．

答案  C

9．某简谐振子，自由振动时的振动图象如图甲中实线所示，而在某驱动力作用下做受迫振动时，稳定后的振动图象如图甲中虚线所示，那么，此受迫振动对应的状态可能是图乙中的(图乙为该简谐振子的共振曲线)(　　)

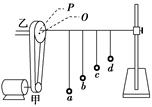
A．a点                                           B．b点

C．c点                                            D．一定不是c点

解析　某简谐振子，设自由振动时的振动周期为T₁，在某驱动力作用下做受迫振动时的周期为T₂，显然T₁<T₂，根据f＝，有f₁>f₂.题图乙中c点对应的是发生共振时驱动力的频率，其等于固有频率f₁；当受迫振动时，驱动力频率为f₂<f₁，故此受迫振动对应的状态可能是题图乙中的a点．故选AD.

答案  AD

10．如图所示，一台玩具电机的轴上安有一个小皮带轮甲，通过皮带带动皮带轮乙转动(皮带不打滑)，皮带轮乙上离轴心O 2 mm处安有一个圆环P.一根细绳一端固定在圆环P上，另一端固定在对面的支架上，绳呈水平且绷直．在绳上悬挂着4个单摆a、b、c、d.已知电动机的转速是149 r/min，甲、乙两皮带轮的半径之比为1∶5,4个单摆的摆长分别是100 cm、80 cm、60 cm、40 cm.电动机匀速转动过程中，振幅最大的单摆是(　　)

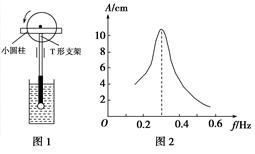
A．单摆a                                        B．单摆b

C．单摆c                                        D．单摆d

解析　电动机的转速是149 r/min，则周期T_甲＝＝ s，甲、乙的半径之比是1∶5，则乙的周期是T_乙＝ s，如果要发生共振，由单摆周期公式T＝2π求得，对应单摆的摆长约为1 m，题中给出的四个单摆中，a最接近，所以a的振幅最大，故选A.

答案  A

11．秒摆摆球质量为0.2 kg，它振动到最大位移时距最低点的高度为0.4 cm，当它完成10次全振动回到最大位移处时，因有阻尼作用，距最低点的高度变为0.3 cm.如果每振动10次补充一次能量，使摆球回到原高度，那么1 min 内总共应补给多少能量？(g＝10 m/s²)

解析  每振动10次要补充的能量为ΔE＝mgΔh＝0.2×10×(0.4－0.3)×10^－2 J＝2.0×10^－3 J．

秒摆的周期为2 s,1 min内完成全振动的次数为30次，

则1 min内总共应补充的能量为E＝3ΔE＝6.0×10^－3 J.

答案  6.0×10^－3 J

12．如图1所示，一个竖直圆盘转动时，固定在圆盘上的小圆柱带动一个T形支架在竖直方向振动，T形支架的下面系着一个弹簧和小球组成的振动系统，小球浸没在水中．当圆盘静止时，让小球在水中振动，球将做阻尼振动．现使圆盘以不同的频率振动，测得共振曲线如图2.(为方便计算g＝9.86 m/s²，π＝3.14)

(1)当圆盘以0.4 s的周期匀速转动，经过一段时间后，小球振动达到稳定，它振动的频率是多少？

(2)若一个单摆的摆动周期与球做阻尼振动的周期相同，该单摆的摆长为多少？(结果保留三位有效数字)

解析  (1)小球振动达到稳定时周期为0.4 s，频率为2.5 Hz.

(2)由图象可以看出单摆的固有频率为0.3 Hz，周期为 s，

由单摆的周期公式T＝2π，解得L＝＝× m≈2.78 m.

答案  (1)2.5 Hz　(2)2.78 m