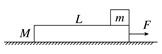专题　牛顿定律的应用 题型分析

专题一 由受力情况确定运动情况

例1 总质量为m＝75 kg的滑雪者以初速度v₀＝8 m/s沿倾角为θ＝37°的斜面向上自由滑行，已知雪橇与斜面间的动摩擦因数μ＝0.25，假设斜面足够长．sin 37°＝0.6.不计空气阻力．试求：

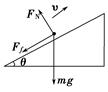
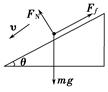
(1)滑雪者沿斜面上滑的最大距离．

(2)若滑雪者滑行至最高点后掉转方向向下自由滑行，求他滑到起点时的速度大小．

解析　(1)上滑过程中，对人进行受力分析，如右图所示，滑雪者受重力mg、支持力F_N、摩擦力F_f作用，设滑雪者的加速度为a₁.根据牛顿第二定律有：

mgsin θ＋F_f＝ma₁，a₁方向沿斜面向下．

在垂直于斜面方向有：F_N＝mgcos θ

又摩擦力F_f＝μF_N

由以上各式解得：a₁＝g(sin θ＋μcos θ)＝8 m/s²

滑雪者沿斜面向上做匀减速直线运动，速度减为零时的位移x＝＝4 m，即滑雪者上滑的最大距离为4 m.

(2)滑雪者沿斜面下滑时，对人受力分析如右图所示，滑雪者受到斜面的摩擦力沿斜面向上，设加速度大小为a₂.根据牛顿第二定律有：

mgsin θ－F_f＝ma₂，a₂方向沿斜面向下．

在垂直于斜面方向有：F_N＝mgcos θ

又摩擦力F_f＝μF_N

由以上各式解得：a₂＝g(sin θ－μcos θ)＝4 m/s²

滑雪者沿斜面向下做初速度为零的匀加速直线运动，滑到出发点时的位移大小为4 m，此时滑雪者的速度大小为v＝＝4 m/s.

答案　(1)4 m　(2)4 m/s

归纳总结：1．物体的运动情况是由受力情况和初始状态共同决定的，如果无法确定物体的初始状态，也就不能正确判断物体的运动情况．

2．分析动力学问题时，要注意区分加速度方向和速度方向．

3．运动和受力紧密联系，受力变，运动情况也变，反之亦如此.

专题二 由运动情况确定受力情况

例2 如图所示的机车，质量为100 t，设它从停车场出发经225 m后速度达到54 km/h，此时，司机关闭发动机，让机车进站，机车又行驶了125 m才停在站上，设机车所受的阻力保持不变，求机车关闭发动机前所受的牵引力．

解析　设机车在加速阶段的加速度为a₁，减速阶段的加速度为a₂

则：v²＝2a₁x₁，v²＝2a₂x₂，解得a₁＝0.5 m/s²，a₂＝0.9 m/s²，

由牛顿第二定律得F－F_f＝ma₁，F_f＝ma₂，解得：F＝1.4×10⁵ N.

答案　1.4×10⁵ N

专题三 连接体问题

例3 如图所示，在光滑的水平面上有一个质量m_C＝4 kg的小车C，物体A和B通过车上的滑轮用细绳相连．它们的质量分别为m_A＝6 kg，m_B＝1 kg，A与C之间的动摩擦因数μ＝，两者之间的最大静摩擦力等于滑动摩擦力，其余摩擦不计，在物体B上作用一个水平恒力可以使三者一起向左做匀加速运动，g取10 m/s²，试求力F的最大值和加速度的最大值．

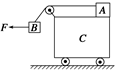
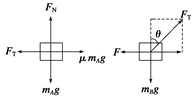
解析　由于A、B、C三者一起向左做匀加速运动，说明三者具有相同的加速度，因此可以把三者看作一个系统，作为一个整体来研究，这个整体的质量等于各物体质量之和，整体在水平方向上所受的外力为F，根据牛顿第二定律即可求出整体的加速度．再隔离A和B分别进行受力分析，即可求出外力F，显然当F最大时，加速度a也最大，此时A刚刚要开始滑动．

设整体运动的最大加速度为a，视A、B、C为一系统，则系统在水平方向上由牛顿第二定律可得

F＝(m_A＋m_B＋m_C)a①

隔离A和B，分别对A、B进行受力分析，如下图所示．

对于A由牛顿第二定律可得F_T－μm_Ag＝m_Aa.②

对于B进行正交分解，由牛顿第二定律得F_Tcos θ－m_Bg＝0③

F－F_Tsin θ＝m_Ba④

由①④两式可得F_Tsin θ＝(m_A＋m_C)a⑤

由③⑤两式可得：F_T＝⑥

由②⑥两式可得：a＝g＝ m/s²＝1.88 m/s²

则F＝(m_A＋m_B＋m_C)a＝11a＝20.7 N

答案　20.7 N　1.88 m/s²

归纳总结：1．连接体：两个(或两个以上)物体相互连接在一起，在外力作用下运动的系统称为连接体．

2．方法：解决连接体有关问题时通常选择整体法和隔离法．一般情况下，求系统内力或加速度时，可选隔离法，求系统外力或加速度时，可选整体法，整体法和隔离法是相对统一、相辅相成的．在解决本来单用隔离法就可以解决的问题时，如果把这两种方法交叉使用，则问题处理起来将更为简捷．

3．当系统中各物体具有相同的加速度，要求系统中某两物体间的作用力时，往往先用整体法求出加速度，再用隔离法求出物体间的相互作用力，即先整体，再隔离．注意隔离时应分析受力少的物体．整体法和隔离法是物理学中的基本方法之一.

专题四 等时圆模型

例4 如图所示，AB和CD为两条光滑斜槽，它们各自的两个端点均分别位于半径为R和r的两个相切的圆上，且斜槽都通过切点P.设有一重物先后沿两个斜槽，从静止出发，由A滑到B和由C滑到D，所用的时间分别为t1和t2，则t1与t2之比为(　　)

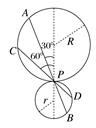
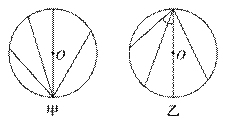
A. 2∶1　　　　　　　　B. 1∶1        C. ∶1                          D. 1∶

解析 设光滑斜槽轨道与水平面的夹角为θ，则物体下滑时的加速度为a＝gsinθ，由几何关系，斜槽轨道的长度s＝2(R＋r)sinθ，由运动学公式s＝at²，得t＝＝＝2，即所用的时间t与倾角θ无关，所以t₁＝t₂，B项正确．

答案　选B

归纳总结：(1)物体沿着位于同一竖直圆上的所有过圆周最低点的光滑弦由静止下滑，到达圆周最低点的时间均相等，且为t＝2(如图甲所示)．

(2)物体沿着位于同一竖直圆上的所有过顶点的光滑弦由静止下滑，到达圆周低端时间相等为t＝2(如图乙所示)．

专题五 相对运动中的动力学问题

例4如下图所示，木板静止于水平地面上，在其最右端放一可视为质点的木块．已知木块的质量m＝1 kg，木板的质量M＝4 kg，长L＝2.5 m，上表面光滑，下表面与地面之间的动摩擦因数μ＝0.2.现用水平恒力F＝20 N向右拉木板，g取10 m/s2，求：

(1)木板加速度的大小；

(2)要使木块能滑离木板，水平恒力F作用的最短时间；

(3)如果其他条件不变，假设木板的上表面也粗糙，其上表面与木块之间的动摩擦因数为μ1＝0.3，欲使木板能从木块的下方抽出，对木板施加的拉力应满足什么条件？

(4)若木板的长度、木块的质量、木板的上表面与木块之间的动摩擦因数、木板与地面间的动摩擦因数都不变，只将水平恒力增加为30 N，则木块滑离木板需要多长时间？

解析  (1)木板受到的摩擦力F_f＝μ(M＋m)g＝10 N木板的加速度a＝＝2.5 m/s².

(2)设拉力F作用时间t后撤去F撤去后，木板的加速度为a′＝－＝－2.5 m/s²

木板先做匀加速运动，后做匀减速运动，且a＝－a′，故at²＝L

解得t＝1 s，即F作用的最短时间为1 s．

(3)设木块的最大加速度为a木块，木板的最大加速度为a木板，则μ1mg＝ma木块

得a木块＝μ1g＝3 m/s2

对木板：F1－μ1mg－μ(M＋m)g＝Ma木板

木板能从木块的下方抽出的条件为a木板>a木块  解得F1>25 N．

(4)木块的加速度a_木块′＝μ₁g＝3 m/s²

木板的加速度a_木板′＝＝4.25 m/s²

木块滑离木板时，两者的位移关系为x_木板－x_木块＝L，即a_木板′t²－a_木块′t²＝L

代入数据解得t＝2 s．

[答案]　(1)2.5 m/s2　(2)1 s　(3)大于25 N　(4)2 s