第二章  章末总结

要点归纳

知识点一、理想气体状态方程与气体实验定律

＝⇒

知识点二、晶体和非晶体的区别

1．区分单晶体、多晶体、非晶体要抓住它们的特点，单晶体的某些物理性质表现出各向异性，多晶体和非晶体都具有各向同性，但多晶体有确定的熔点，非晶体没有．

2．从微观角度(如温度是分子平均动能的标志，克服分子力做功，势能增加)分析分子动能，分子势能的变化，从客观(如吸热、放热)上分析物体内能的变化．

知识点三、浸润、不浸润及表面张力

1．在分析这类现象时，应抓住两点：

(1)液体表面因存在表面张力而具有收缩趋势；

(2)浸润液体的附着层内因存在排斥力而具有扩张趋势；不浸润液体的附着层内因存在收缩力而具有收缩趋势．

2．毛细现象是浸润与不浸润和表面张力的共同作用而形成的，浸润液体跟毛细管内壁接触时，引起液体附着层扩张，而表面张力的作用是使液体与毛细管内壁的接触面减小而收缩，从而使液面弯曲对液柱起提升作用，而且毛细管内径越小，提升越高．与此相反，不浸润的液体与毛细管内壁接触时，引起液体附着层收缩，而表面张力也使液面收缩，从而使液面弯曲对液柱起压低下降的作用，而且毛细管内径越小，压低下降的高度也越大．

 

 

 

应用状态方程解题的一般步骤

(1)明确研究对象，即某一定质量的理想气体；

(2)确定气体在始、末状态的参量p₁、V₁、T₁及p₂、V₂、T₂；

(3)由状态方程列式求解；

(4)讨论结果的合理性．

知识点三、应用状态方程解题的一般步骤

拓展二　变质量问题

分析变质量问题时，可以通过巧妙选择合适的研究对象，使这类问题转化为定质量的气体问题，用理想气体状态方程求解．

1．打气问题．

向球、轮胎中充气是一个典型的气体变质量的问题．只要选择球内原有气体和即将打入的气体作为研究对象，就可以把充气过程中的气体质量变化的问题转化为定质量气体的状态变化问题．

2．抽气问题．

从容器内抽气的过程中，容器内的气体质量不断减小，这属于变质量问题．分析时，将每次抽气过程中抽出的气体和剩余气体作为研究对象，质量不变，故抽气过程可看做是等温膨胀的过程．

拓展三　气缸类问题的处理方法

解决气缸类问题的一般思路：

1．弄清题意，确定研究对象．一般来说，研究对象分两类：一类是热学研究对象(一定质量的理想气体)；另一类是力学研究对象(气缸、活塞或某系统)．

2．分析清楚题目所述的物理过程，对热学研究对象分析清楚初、末状态及状态变化过程，依气体定律列出方程；对力学研究对象要正确地进行受力分析，依据力学规律列出方程．

3．注意挖掘题目中的隐含条件，如几何关系等，列出辅助方程．

4．多个方程联立求解．对求解的结果注意检验它们的合理性．

 

 

 

 

典例分析

一、图像问题

例1 一定质量的理想气体由状态A变为状态D，其有关数据如图甲所示，若状态D的压强是2×10⁴ Pa.

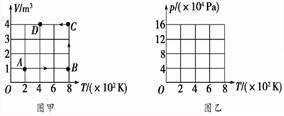
(1)求状态A的压强．

(2)请在图乙中画出该状态变化过程的p－T图象，并分别标出A、B、C、D各个状态，不要求写出计算过程．

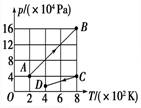
解析 (1)根据理想气体状态方程：＝，

则p_A＝＝4×10⁴Pa.

(2)p－T图象及A、B、C、D各个状态如图所示．

答案 (1)4×10⁴ Pa　(2)如上图所示

归纳总结：1．图象上的一个点表示一定质量气体的一个平衡态，它对应着三个状态参量；图象上的某一条直线或曲线表示一定质量气体状态变化的一个过程．

2．在V－T或P－T图象中，比较两个状态的压强或体积大小，可以用这两个状态到原点连线的斜率大小来判断．斜率越大，压强或体积越小；斜率越小，压强或体积越大．

二、活塞问题

例2　一竖直放置、缸壁光滑且导热的柱形气缸内盛有一定量的氮气，被活塞分隔成Ⅰ、Ⅱ两部分．达到平衡时，这两部分气体的体积相等，上部气体的压强为p₁₀，如图(a)所示，若将气缸缓慢倒置，再次达到平衡时，上下两部分气体的体积之比为3∶1，如图(b)所示．设外界温度不变，已知活塞面积为S，重力加速度大小为g，求活塞的质量．

解析  设活塞的质量为m，气缸倒置前下部气体的压强为p₂₀，倒置后上下气体的压强分别为p₂、p₁，由力的平衡条件有p₂₀＝p₁₀＋，p₁＝p₂＋，

倒置过程中，两部分气体均经历等温过程，设气体的总体积为V₀，由玻意耳定律得

p₁₀＝p₁，p₂₀＝p₂，解得m＝.

答案 

归纳总结：两部分气体问题中，对每一部分气体来讲独立满足＝C.两部分气体往往满足一定的联系：如压强关系，体积关系，从而再列出联系方程即可．

三、打起问题

例3　某种喷雾器的贮液筒的总容积为7.5 L，如图所示，装入6 L的药液后再用密封盖将贮液筒密封，与贮液筒相连的活塞式打气筒每次能压入300 cm³，1 atm的空气，设整个过程温度保持不变．

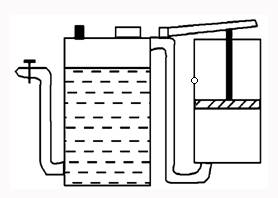
(1)要使贮气筒中空气的压强达到4 atm，打气筒应打压几次？

(2)在贮气筒中空气的压强达到4 atm时，打开喷嘴使其喷雾，直到内外气体压强相等，这时筒内还剩多少药液？

解析  (1)设每打一次气，贮液筒内增加的压强为p，

由玻意耳定律得：1 atm×300 cm³＝1.5×10³ cm³×p.

p＝0.2 atm，需打气次数n＝＝15.

(2)设停止喷雾时贮液筒内气体体积为V，

由玻意耳定律得：

4 atm×1.5 L＝1 atm×V，

V＝6 L.

故还剩贮液7.5 L－6 L＝1.5 L.

答案  (1)15　(2)1.5 L

归纳总结：解决气体问题要么利用气体的实验定律，要么利用理想气体状态方程，但前提条件都是定质量问题．处理所有变质量问题时，首先要转化为定质量问题．

四、气体中牛顿第二定律的应用

例4　如图，一汽缸水平固定在静止的小车上，一质量为m、面积为S的活塞将一定量的气体封闭在汽缸内，平衡时活塞与汽缸底相距L.现让小车以一较小的水平恒定加速度向右运动，稳定时发现活塞相对于汽缸移动了距离d.已知大气压强为p₀，不计汽缸和活塞间的摩擦；且小车运动时，大气对活塞的压强仍可视为p₀；整个过程温度保持不变．求小车加速度的大小．

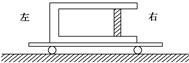
解析　设小车加速度大小为a，稳定时汽缸气体的压强为p₁，活塞受到汽缸内、外气体的压力分别为f₁＝p₁S①

f₀＝p₀S②

由牛顿第二定律得f₁－f₀＝ma③

小车静止时，在平衡情况下，汽缸内气体的压强应为p₀，由玻意耳定律得

p₁V₁＝p₀V④

式中V＝SL⑤

V₁＝S(L－d)⑥

联立①②③④⑤⑥式得a＝

答案　

归纳总结：这类问题的一般解题思路：首先明确研究对象，然后明确初、末状态及状态参量，再利用玻意耳定律列方程，从而联立求解．对于充气、抽气类问题可以通过灵活选取研究对象，化变质量为一定质量，进行解答．

五、理想气体状态方程

例5　如图，绝热气缸A与导热气缸B均固定于地面，由刚性杆连接的绝热活塞与两气缸间均无摩擦．两气缸内装有处于平衡状态的理想气体，开始时体积均为V₀、温度均为T₀.缓慢加热A中气体，停止加热达到稳定后，A中气体压强为原来的1.2倍．设环境温度始终保持不变，求气缸A中气体的体积V_A和温度T_A.

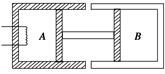
解析　设初态压强为p₀，膨胀后A、B压强相等

p_B＝1.2p₀

B中气体始、末状态温度相等，p₀V₀＝1.2p₀(2V₀－V_A)

得V_A＝V₀

A部分气体满足＝，得T_A＝1.4T₀.

方法指导　这类问题的处理方法：确定研究对象后，再分析初、末状态的变化．若p、V、T三个量都发生变化，则选用＝常数列方程．若某一个量不变，则选用合适的定律，列方程求解，在涉及两部分气体时，要注意找出两部分气体的联系，再列出联立方程．

答案　V₀　1.4T₀

六、对气体压强的理解

例6　如图所示，两个完全相同的圆柱形密闭容器，甲中装有与容器容积相等的水，乙中充满空气，试问：

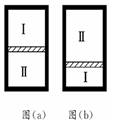
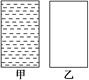
(1)两容器各侧壁压强的大小关系及压强的大小决定于哪些因素？(容器容积恒定)

(2)若让两容器同时做自由落体运动，容器侧壁上所受压强将怎样变化？

解析　(1)对甲容器，上壁的压强为零，底面的压强最大，其数值为p＝ρgh(h为上下底面间的距离)．侧壁的压强自上而下，由小变大，其数值大小与侧壁上各点距水面的竖直距离x的关系是p＝ρgx.对乙容器，各处器壁上的压强大小都相等，其大小决定于气体的分子密集程度和温度．

(2)甲容器做自由落体运动时器壁各处的压强均为零．乙容器做自由落体运动时，器壁各处的压强不发生变化．

答案　见解析

归纳总结：(1)掌握好气体分子压强的微观解释．(2)千万不要把液体和气体压强混淆，要从产生原因上加以区别．

七、液体张力

例7　下列现象是因液体的表面张力所致的是(　　)

A．小孩用细管蘸肥皂水，吹出圆形的肥皂泡

B．小木船漂浮在水面上

C．缝衣针漂浮在水面上

D．透过布制的伞面能看见纱线间的缝隙，但是使用时伞面却不漏雨水

E．注满氢气的彩色气球呈现球形

F．在水平玻璃板上，散落的水银呈球形或椭球形

解析　小木船浮在水面上是因为受到水的浮力，B错；氢气球呈球形是大气压力和弹力的共同作用，显然不是液体的表面张力所致，E错．缝衣针漂浮在水面上，有缝隙的伞面不漏水，散落的水银呈球形等都是表面张力作用．

答案　ACDF

归纳总结：表面张力是液体表面特有的现象，就像张紧的薄膜一样．分析问题时，要注意区分水的浮力与表面张力的不同，表面张力跟橡皮膜的不同．