第3节　动量守恒定律

知识点归纳

知识点一、系统、内力和外力

1．系统：碰撞问题的研究对象不是一个物体，而是两个或两个以上的物体．我们说这两个物体组成了一个力学系统．

2．内力：系统内物体之间的相互作用力．

3．外力：除系统内物体之间的相互作用力之外的其他力叫作外力．

知识点二、动量守恒定律

(1)内容：如果一个系统不受外力，或者所受外力的矢量和为零，这个系统的总动量保持不变．

(2)表达式：p＝p′.对两个物体组成的系统，可写为：m1v1＋m2v2＝m1v1′＋m2v2′.

知识点三、动量守恒定律成立的条件

动量守恒定律是有条件的，应用时一定要首先判断系统是否满足守恒条件。

a．系统不受外力作用，这是一种理想化的情形，如宇宙中两星球的碰撞，微观粒子间的碰撞都可视为这种情形。

b．系统虽然受到了外力的作用，但所受外力的和——即合外力为零。像光滑水平面上两物体的碰撞就是这种情形，两物体所受的重力和支持力的合力为零。

c．系统所受的外力远远小于系统内各物体间的内力时，系统的总动量近似守恒。抛出去的手榴弹在空中爆炸的瞬间，弹片所受火药的内力远大于其重力，重力完全可以忽略不计，动量近似守恒。

d．系统所受的合外力不为零，即F外≠0，但在某一方向上合外力为零(Fx＝0或Fy＝0)，则系统在该方向上动量守恒。

e．系统受外力，但在某一方向上内力远大于外力，也可认为在这一方向上系统的动量守恒。

知识点四、动量守恒定律性质

(1)矢量性：定律的表达式是一个矢量式。

a．该式说明系统的总动量在任意两个时刻不仅大小相等，而且方向也相同。

b．在求系统的总动量p＝p1＋p2＋…时，要按矢量运算法则计算。

(2)相对性：动量守恒定律中，系统中各物体在相互作用前后的动量，必须相对于同一惯性系，各物体的速度通常均为相对于地的速度。

(3)同时性：动量守恒定律中p1、p2…必须是系统中各物体在相互作用前同一时刻的动量，p1′、p2′…必须是系统中各物体在相互作用后同一时刻的动量。

(4)普适性：动量守恒定律不仅适用于两个物体组成的系统，也适用于多个物体组成的系统。不仅适用于宏观物体组成的系统，也适用于微观粒子组成的系统。

典例分析

一、动量守恒定律成立的条件

例1  如图所示，小车与木箱静止放在光滑的水平冰面上，现有一男孩站在小车上向右用力迅速推出木箱，关于上述过程，下列说法正确的是(　　)

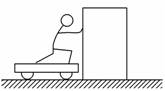
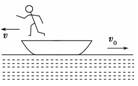
A．男孩和木箱组成的系统动量守恒  

B．小车与木箱组成的系统动量守恒

C．男孩、小车与木箱三者组成的系统动量守恒

D．木箱的动量增量与男孩、小车的总动量增量相同

解析　在男孩站在小车上用力向右迅速推出木箱的过程中，男孩和木箱组成的系统所受合外力不为零，系统动量不守恒，故A错误；小车与木箱组成的系统所受合外力不为零，系统动量不守恒，故B错误；男孩、小车与木箱三者组成的系统所受合外力为零，系统动量守恒，故C正确；木箱、男孩、小车组成的系统动量守恒，木箱的动量增量与男孩、小车的总动量增量大小相等，方向相反，故D错误．

答案　C

归纳总结：判断系统动量是否守恒的方法

(1)直接分析系统在所研究的过程中始、末状态的动量，分析动量是否守恒．

(2)分析系统在所研究的过程中的受力情况，看系统的受力情况是否符合动量守恒的条件．

二、宇宙中的动量守恒

例2  如图所示，进行太空行走的宇航员A和B的质量分别为80 kg和100 kg，他们携手远离空间站，相对空间站的速度为0.1 m/s. A 将B 向空间站方向轻推后，A的速度变为0.2 m/s，求此时B 的速度大小和方向．

解析：取远离空间站的方向为正方向，则A和B开始的速度为v₀＝0.1 m/s远离空间站，推开后，A的速度v_A＝0.2 m/s，此时B的速度为v_B，

根据动量守恒定律有：(m_A＋m_B)v₀＝m_Av_A＋m_Bv_B

代入数据解得：v_B＝

＝ m/s＝0.02 m/s，

即B的速度方向沿远离空间站方向．

答案：0.02 m/s，远离空间站

归纳总结：本题以航天为背景，考查动量守恒定律，要注意选取正方向，用正负号表示速度的方向．

三、动量守恒定律应用中的临界问题

例3  一条滑道由一段半径 R＝0.8 m的 1/4 圆弧轨道和一段长为 L＝3.2 m 水平轨道 MN 组成，在 M点处放置一质量为 m 的滑块 B，另一个质量也为 m 的滑块 A 从左侧最高点无初速度释放，A、B 均可视为质点．已知圆弧轨道光滑，且 A 与 B 之间的碰撞无机械能损失(取 g＝10 m/s2)．

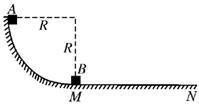
(1)求A滑块与B滑块碰撞后的速度v′A 和v′B；

(2)若A滑块与B滑块碰撞后，B滑块恰能达到N 点，则MN 段与 B 滑块间的摩擦因数μ的大小为多少？

解析 (1)设A与B相碰前的速度为v_A，A从圆弧轨道上滑下时机械能守恒，故mv＝mgR①

A与B相碰时，动量、机械能守恒mv_A＝mv′_A＋mv′_B②

mv＝mv′＋mv′③

由①～③得v′_A ＝0，v′_B＝4 m/s

(2)B碰撞后到达N点速度为0，由动能定理得－fL＝0－mv′④

其中f＝μmg⑤

由④⑤得μ＝0.25.

答案  (1) 0  4 m/s   (2)0.25

四、多个物体组成的系统动量守恒问题

例4  如图所示，三辆完全相同的平板小车a、b、c成一直线排列，静止在光滑水平面上。c车上有一小孩跳到b车上，接着又立即从b车跳到a车上。小孩跳离c车和b车时对地的水平速度相同。他跳到a车上相对a车保持静止，此后(　　)

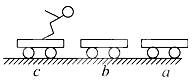
A．a、b两车运动速率相等

B．a、c两车运动速率相等

C．三辆车的速率关系vc>va>vb

D．a、c两车运动方向相反

解析 若人跳离b、c车时速度为v，由动量守恒定律知，人和c车组成的系统：0＝－M_车v_c＋m_人v

对人和b车：m_人v＝－M_车v_b＋m_人v

对人和a车：m_人v＝(M_车＋m_人)·v_a

所以：v_c＝，v_b＝0，v_a＝

即v_c>v_a>v_b，并且v_c与v_a方向相反。

答案 CD

五、某一方向上的动量守恒问题

例5  如图所示，一个质量为m的木块，从半径为R、质量为M的光滑圆槽顶端由静止滑下．已知圆槽可沿着光滑水平面自由滑动．求木块从槽口滑出时的速度大小为多少？

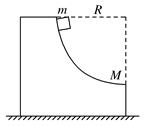
解析　木块从开始下滑到脱离槽口的过程中，木块和槽所组成的系统水平方向不受外力，水平方向动量守恒．设木块滑出槽口时的速度为v₂，槽的速度为v₁，

则mv₂－Mv₁＝0①

又木块下滑时，只有重力做功，系统机械能守恒，即mgR＝mv＋Mv②

联立①②两式解得木块滑出槽口的速度v₂＝

答案　

自我检测

1．关于系统动量守恒的条件，下列说法中正确的是(　　)

A．只要系统内存在摩擦力，系统的动量就不可能守恒

B．只要系统中有一个物体具有加速度，系统的动量就不守恒

C．只要系统所受的合外力为零，系统的动量就守恒

D．系统中所有物体的加速度都为零时，系统的总动量不一定守恒

解析 根据动量守恒的条件即系统所受外力的矢量和为零可知，选项C正确；系统内存在摩擦力，与系统所受外力无关，选项A错误；系统内各物体之间有着相互作用，对单个物体来说，合外力不一定为零，加速度不一定为零，但整个系统所受的合外力仍可为零，动量守恒，选项B错误；系统内所有物体的加速度都为零时，各物体的速度恒定，动量恒定，总动量一定守恒，选项D错误．

答案 C

2．两位同学穿旱冰鞋，面对面站立不动，互推后向相反的方向运动，不计摩擦阻力，下列判断正确的是(　　)

A．互推后两同学总动量增加

B．互推后两同学动量大小相等，方向相反

C．分离时质量大的同学的速度小一些

D．互推过程中机械能守恒

解析 对两同学所组成的系统，互推过程中，合外力为零，总动量守恒，故A错；两同学动量的变化量大小相等，方向相反，故B、C正确；互推过程中机械能增大，故D错误．

答案 BC

3．将静置在地面上，质量为M(含燃料)的火箭模型点火升空，在极短时间内以相对地面的速度v₀竖直向下喷出质量为m的炽热气体．忽略喷气过程重力和空气阻力的影响，则喷气结束时火箭模型获得的速度大小是(　　)

A.v₀        B.v₀

C.v₀    D.v₀

解析 取向上为正方向，由动量守恒定律得：0＝(M－m)v－mv₀.

则火箭速度：v＝.故选D.

答案 D

4．如图，质量为M的小船在静止水面上以速率v₀向右匀速行驶，一质量为m的救生员站在船尾，相对小船静止．若救生员以相对水面速率v水平向左跃入水中，则救生员跃出后小船的速率为(　　)

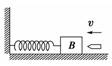
A．v₀＋v                B．v₀－v

C．v₀＋(v₀＋v)           D．v₀＋(v₀－v)

解析 人在跃出的过程中，船、人组成的系统水平方向上动量守恒，规定向右为正方向．

则：(M＋m)v₀＝Mv′－mv，解得：v′＝v₀＋(v₀＋v)故选C.

答案 C

5．沿水平方向飞行的手榴弹，它的速度是20 m/s，此时在空中爆炸，分裂成1 kg和0.5 kg的两块，其中0.5 kg的那块以40 m/s的速率沿原来速度相反的方向运动，此时另一块的速率为(　　)

A．10 m/s     B．30 m/s     C．50 m/s     D．70 m/s

解析 手榴弹爆炸，外力远小于内力，可近似地看作动量守恒，

根据：(m₁＋m₂)v＝m₁v₁′＋m₂v₂′，可得：

v₂′＝＝ m/s＝50 m/s.

答案 C

6．在如图所示的装置中，木块B与水平桌面间的接触是光滑的，子弹A沿水平方向射入木块后留在其中，将弹簧压缩到最短。若将子弹、木块和弹簧合在一起作为系统，则此系统在从子弹开始射入到弹簧被压缩至最短的整个过程中(　　)

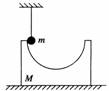
A．动量守恒，机械能守恒

B．动量不守恒，机械能不守恒

C．动量守恒，机械能不守恒

D．动量不守恒，机械能守恒

解析 子弹射入木块是瞬间完成的，这个过程相当于子弹与木块发生一次完全非弹性碰撞，动量守恒，机械能不守恒，一部分动能转化为内能，之后木块(连同子弹)压缩弹簧，将其动能转化为弹性势能，这个过程机械能守恒，但动量不守恒，由于左侧挡板的支持力的冲量作用，使系统的动量不断减少，所以整个过程中，动量和机械能均不守恒。

答案 B

7．如图所示，光滑圆槽质量为M，静止在光滑的水平面上，其内表面有一小球被细线吊着恰位于槽的边缘处，如将线烧断，小球滑到另一边的最高点时，圆槽的速度为(　　)

 

A．0　　　　　　　　                          B．向左

C．向右                                                 D．不能确定

解析 把小球m和物体M作为一个系统，因水平面光滑，故系统水平方向不受外力，水平方向动量守恒。

答案 A

8．一颗子弹水平射入置于光滑水平面上的木块A并留在其中，木块A、B用一根弹性良好的轻质弹簧连在一起，如图所示．则在子弹射入木块A及弹簧被压缩的过程中，对子弹、两木块和弹簧组成的系统，下列说法正确的是(　　)

 

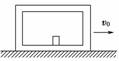
A．动量守恒，机械能守恒

B．动量不守恒，机械能守恒

C．动量守恒，机械能不守恒

D．无法判定动量、机械能是否守恒

解析　动量守恒的条件是系统不受外力或所受外力的合力为零，本题中子弹、两木块、弹簧组成的系统，水平方向上不受外力，竖直方向上所受外力的合力为零，所以动量守恒．机械能守恒的条件是除重力、弹力对系统做功外，其他力对系统不做功，本题中子弹射入木块过程中克服摩擦力做功，有部分机械能转化为内能(发热)，所以系统的机械能不守恒，故C正确，ABD错误．

答案　C

9．如图所示，一个木箱原来静止在光滑水平面上，木箱内粗糙的底板上放着一个小木块．木箱和小木块都具有一定的质量．现使木箱获得一个向右的初速度v₀，则(　　)

A．小木块和木箱最终都将静止  

B．小木块最终将相对木箱静止，二者一起向右运动

C．小木块在木箱内壁将始终来回往复碰撞，而木箱一直向右运动

D．如果小木块与木箱的左壁碰撞后相对木箱静止，则二者将一起向左运动

解析　最终，木箱和小木块都具有向右的动量，并且相互作用的过程中总动量守恒，选项AD错误；由于小木块与底板间存在摩擦，小木块最终将相对木箱静止，选项B正确，选项C错误．

答案　B

10．甲、乙两人站在光滑的水平冰面上，他们的质量都是M，甲手持一个质量为m的球，现甲把球以对地为v的速度传给乙，乙接球后又以对地为2v的速度把球传回甲，甲接到球后，甲、乙两人的速度大小之比为(忽略空气阻力)(　　)

A．　　　　　　                          B．

C．　                                        D．

解析　甲、乙之间传递球的过程中，不必考虑过程中的细节，只考虑初状态和末状态的情况．研究对象是由甲、乙二人和球组成的系统，开始时的总动量为零，在任意时刻系统的总动量都为零．设甲的速度大小为v_甲，乙的速度大小为v_乙，二者方向相反，根据动量守恒得(M＋m)v_甲－Mv_乙＝0，则＝，选项D正确．

答案　D

11．一人站在静止于冰面的小车上，人与车的总质量M＝70 kg，当它接到一个质量m＝20 kg、以速度v₀＝5 m/s迎面滑来的木箱后，立即以相对于自己v′＝5 m/s的速度逆着木箱原来滑行的方向推出，不计冰面阻力。则小车获得的速度是多大？方向如何？

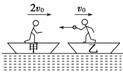
解析 设推出木箱后小车的速度为v，此时木箱相对地面的速度为(v′－v)，由动量守恒定律得mv₀＝Mv－m(v′－v)

v＝＝m/s＝2.2m/s。

与木箱的初速度v₀方向相同。

答案 2.2m/s　方向与木箱的初速度v₀相同

12．如图所示，甲、乙两船的总质量(包括船、人和货物)分别为10m、12m，两船沿同一直线同一方向运动，速度分别为2v₀、v₀.为避免两船相撞，乙船上的人将一质量为m的货物沿水平方向抛向甲船，甲船上的人将货物接住，求抛出货物的最小速度．(不计水的阻力)

解析 设乙船上的人抛出货物的最小速度大小为v_min，抛出货物后船的速度为v₁，甲船上的人接到货物后船的速度为v₂，由动量守恒定律得：

12mv₀＝11mv₁－mv_min①

10m×2v₀－mv_min＝11mv₂②

为避免两船相撞应满足：v₁＝v₂③

联立①②③式得：v_min＝4v₀④

答案 4v₀