第2节　全反射

知识点归纳

知识点一、全反射

1．光密介质和光疏介质

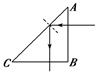
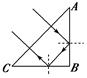
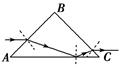
2.全反射及发生条件

(1)全反射及临界角的概念

①全反射：光从光密介质射入光疏介质时，若入射角增大到某一角度，折射光线就会消失，只剩下反射光线的现象．

②临界角：刚好发生全反射，即折射角等于90°时的入射角．用字母C表示．

(2)全反射的条件：要发生全反射，必须同时具备两个条件：

①光从光密介质射入光疏介质．

②入射角等于或大于临界角．

(3)临界角与折射率的关系：光由介质射入空气(或真空)时，sin C＝(公式)．

知识点二、全反射的应用

1．全反射棱镜

(1)形状：截面为等腰直角三角形的棱镜．

(2)光学特性：①当光垂直于截面的直角边射入棱镜时，光在截面的斜边上发生全反射，光射出棱镜时，传播方向改变了90°．②当光垂直于截面的斜边射入棱镜时，在两个直角边上各发生一次全反射，使光的传播方向改变了180°．

2．全反射棱镜的作用及应用

(1)作用：横截面是等腰直角三角形的棱镜叫全反射棱镜，全反射棱镜是一种特殊的棱镜，在光学仪器中用来改变光的方向．

(2)应用：对于精密的光学仪器，如照相机、望远镜、显微镜等，就需要用全反射棱镜代替平面镜，以消除多余的像．

3．光通过全反射棱镜时的几种方式：

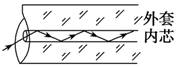
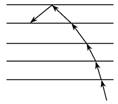
知识点三、光导纤维

(1)光导纤维的传播原理：光由一端进入，在两层的界面上经过多次全反射，从另一端射出．光导纤维可以远距离传播光，光信号又可以转换成电信号，进而变为声音、图像．如果把许多(上万根)光导纤维合成一束，并使两端的纤维按严格相同的次序排列．就可以传播图像．

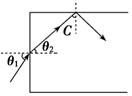
(2)光导纤维的折射率

设光导纤维的折射率为n，当入射角为θ₁时，进入端面的折射光线传到侧面时恰好发生全反射，如图所示，则有sin C＝，n＝，C＋θ₂＝90°，由以上各式可得sin θ₁＝.

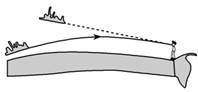
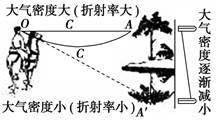
由图可知：当θ₁增大时，θ₂增大，而从纤维射向真空中光线的入射角θ减小，当θ₁＝90°时，若θ＝C，则所有进入纤维中的光线都能发生全反射，即解得n＝，以上是光从纤维射向真空时得到的折射率，由于光导纤维包有外套，外套的折射率比真空的折射率大，因此光导纤维折射率要比大些．

知识点四、日常生活中的全反射

1．透明体中的气泡看起来特别亮

光照射到透明体上时，光线绝大多数穿过透明体．若透明体中有气泡，进入透明体中的部分光线射到空气泡上时，由于透明体的折射率大于气泡的折射率，若入射角大于或等于临界角，这部分光会发生全反射，然后射入人眼，由于气泡处反射回来的光比没有气泡处强得多，所以气泡看起来特别亮．

2．海市蜃楼

(1)气候条件：当大气比较平静且海面与上层空气温差较大时，空气的密度随温度的升高而减小，对光的折射率也随之减小．因海面上的空气温度比空中低，空气的下层比上层折射率大．我们可以粗略地把空中的大气分成许多水平的空气层，如图所示．

(2)光路分析：远处的景物反射的光线射向空中时，不断被折射，射向折射率较小的上一层的入射角越来越大，当光线的入射角增大到临界角时，就会发生全反射现象，光线就会从高空的空气层中通过空气的折射逐渐返回折射率较大的下一层．

(3)虚像的形成：当光线进入人的眼睛时，人总认为光是从其反向延长线方向发射而来的，所以地面附近的观察者就可以观察到虚像，且虚像成像于远处的半空中，这就是海市蜃楼．如图所示．

3．沙漠蜃景

夏日的正午烈日当头，沙漠表面被晒得非常热，其温度很快上升，由此沙漠地表处温度很高，故大气层下层空气密度小而上层空气密度逐渐增大，则从沙漠地面向上的空气的折射率由小到大连续变化．从远处物体或蓝色天空斜射向地面的光线进入折射率逐渐减小的热空气层被折射后，其折射角大于入射角且折射角与入射角均逐渐增大，使传播方向总要向上偏一些，而且入射光线可能在沙漠地面附近发生全反射．由于人眼不能看到光线的曲折，而是按直线进入人眼中的光线射来的方向看到物体，所以人看到这些光线好像是由他的前方射来的，于是人们就看到前方远处物体的倒影或者感觉到前方的沙漠中出现了一片蔚蓝发光的湖面(实际上是天空的虚像)，如图所示这就是“沙漠蜃景”形成的光路图．

     

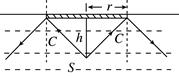
知识点五、应用全反射测定物体的折射率

方法一：利用全反射测定液体的折射率

用一个圆形软木塞，在其中心处竖直地倒插一枚大头针，使其漂浮在待测液体中，如图所示，调整大头针的插入深度，使观察者在液体的上方任一位置恰好都看不到大头针的顶部S，此时，从S发出的光线，在木塞边缘的液体处恰好发生了全反射．此时的入射角C即为该液体发生全反射的临界角．测出木塞的半径r和大头针顶部的深度h，则有

sinC＝＝，故液体的折射率：n＝.

方法二：利用全反射测定半圆形玻璃砖的折射率

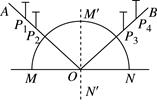
将半圆形玻璃砖放在白纸上，记下直径的位置MN，MN即为界面．竖直插下大头针P₁和P₂，使P₁和P₂的延长线过玻璃的圆心O.以O为轴缓慢转动玻璃砖，使观察者在另一侧的任何位置都不能同时观察到P₂和P₁的像，此时过P₂和P₁的光线AO在界面MN上发生了全反射，此时的入射角AOM′即为全反射的临界角C，如图所示．固定玻璃砖，在玻璃砖的同侧的另一方向竖直插下大头针P₃和P₄，使P₃挡住通过玻璃砖观察到的P₂和P₁的像，使P₄挡住P₃和P₁，P₂的像．过大头针P₃和P₄的光线BO，即为AO的反射光线．测出∠AOB，∠AOB为临界角的两倍，则玻璃砖的折射率：n＝＝.

典例分析

一、全反射

例1  如图所示，一束入射光AO从某种介质以入射角α射入空气，以O点为圆心，R₁为半径画圆C₁，与折射光线OB交于M点，过M点向两介质的交界面作垂线，与入射光线AO的延长线交于N点，以O点为圆心，ON为半径画另一个圆C₂，测得该圆的半径为R₂，下列判断正确的是(　　)

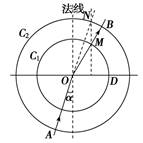
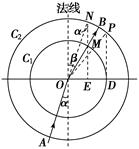
A．该介质的折射率为

B．若光由介质射入空气发生全反射，则临界角的正弦值为sin C＝

C．若过圆C₁与界面的交点D作界面的垂线交圆C₂于P点，则OP与法线所夹的锐角等于全反射的临界角

D．若入射光的强度保持不变，逐渐增大入射角α，则折射光的强度将逐渐增加

解析　由图可知，介质的折射率n＝，而sin β＝，sin α＝，得n＝，A正确；全反射的临界角sin C＝，sin C＝，B正确；过D作DP，sin∠OPD＝，故∠OPD＝∠C，因而C选项正确；当α增大时，折射光强度应减弱，D错误．

答案　ABC

归纳总结：解答全反射类问题的技巧

(1)光必须从光密介质射入光疏介质．

(2)入射角大于或等于临界角．

(3)利用好光路图中的临界光线，准确地判断出恰好发生全反射的光路图是解题的关键，且在作光路图时比例与实际相符，这样更有利于问题的分析．

二、光导纤维

例2  如图所示，一根长为l＝5.0 m的光导纤维用折射率n＝的材料制成．一束激光由其左端的中心点以45°的入射角射入光导纤维内，经过一系列全反射后从右端射出，求：

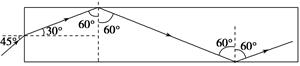
(1)该激光在光导纤维中的速度v.

(2)该激光在光导纤维中传输所经历的时间．

解析　(1)由n＝可得v≈2.1×10⁸ m/s.

(2)由n＝可得光线从左端面射入后的折射角为30°，射到侧面时的入射角为60°，大于临界角45°，因此发生全反射．同理光线每次在侧面都将发生全反射，直到光线到达右端面，其光路如图所示．由几何关系可以求出光线在光导纤维中通过的总路程s＝，因此该激光在光导纤维中传输所经历的时间t＝≈2.7×10^－8 s.

答案　(1)2.1×10⁸ m/s　(2)2.7×10^－8 s

归纳总结：

(1)发生全反射的条件是光由光密介质射向光疏介质，且入射角大于或等于临界角．

(2)光导纤维利用了光的全反射，所以内芯的折射率一定大于外套的折射率．

自我检测

1．下列说法正确的是(　　)

A．因为水的密度大于酒精的密度，所以水是光密介质

B．因为水的折射率小于酒精的折射率，所以水对酒精来说是光疏介质

C．同一束光，在光密介质中的传播速度较大

D．同一束光，在光密介质中的传播速度较小

解析　因为水的折射率小于酒精的折射率，所以水对酒精来说是光疏介质，A错误，B正确；由v＝可知，同一束光在光密介质中的传播速度较小，故C错误，D正确。

答案　BD

2．关于全反射，下列说法中正确的是(　　)

A．发生全反射时，仍有折射光线，只是折射光线非常弱，因此可以认为不存在折射光线而只有反射光线

B．光从光密介质射向光疏介质时，一定会发生全反射现象

C．光从光疏介质射向光密介质时，不可能发生全反射现象

D．水或玻璃中的气泡看起来特别亮，就是因为光从水或玻璃射向气泡时，在界面处发生了全反射

解析　全反射发生的条件是光从光密介质射向光疏介质，且入射角大于或等于临界角，发生全反射时全部光线均不进入光疏介质，故A、B错误，C正确；当光线经由水或玻璃射向气泡时，由于水和玻璃的折射率均大于空气的折射率，部分光线在界面处发生全反射，所以气泡会显得特别亮，D正确。

答案　CD

3．光在某种介质中传播时的速度为1.5×10⁸ m/s，那么，光从此种介质射向空气并发生全反射的临界角应为(　　)

A．60°  B．45°  C．30°  D．75°

解析　根据n＝，sinC＝，得sinC＝＝＝，解得C＝30°，C正确。

答案　C

4．光导纤维的结构如图所示，其内芯和外套材料不同，光在内芯中传播。以下关于光导纤维的说法正确的是(　　)

A．内芯的折射率比外套的大，光传播时在内芯与外套的界面上发生全反射

B．内芯的折射率比外套的小，光传播时在内芯与外套的界面上发生全反射

C．内芯的折射率比外套的小，光传播时在内芯与外套的界面上发生折射

D．内芯的折射率与外套的相同，外套的材料有韧性，可以起保护作用

解析　光导纤维是利用光从光密介质(内芯)射入光疏介质(外套)时发生全反射的现象来传递信息的，B、C、D错误，A正确。

答案　A

5．如图所示，自行车的尾灯采用了全反射棱镜的原理。它虽然本身不发光，但在夜间骑行时，从后面开来的汽车发出的强光照到尾灯后，会有较强的光被反射回去，使汽车司机注意到前面有自行车。下面说法中正确的是(　　)

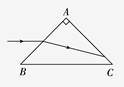
A．汽车灯光应从左面射过来在尾灯的左表面发生全反射

B．汽车灯光应从左面射过来在尾灯的右表面发生全反射

C．汽车灯光应从右面射过来在尾灯的左表面发生全反射

D．汽车灯光应从右面射过来在尾灯的右表面发生全反射

解析　汽车灯光应从右面射向自行车尾灯，光在尾灯内部左表面发生全反射，使自行车后面的汽车司机发现前面有自行车，避免事故的发生，A、B、D错误，C正确。

答案　C

6．为测量一块等腰直角三棱镜△ABC的折射率，用一束光沿平行于BC边的方向射向AB边，如图所示。光束进入棱镜后射到AC边时，刚好能发生全反射。该棱镜的折射率为(　　)

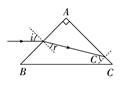
A.  B.  C.  D.

解析　作出光路图，如图所示，根据题意和几何关系可知，i＝45°，n＝，sinC＝，r＝90°－C，联立以上各式，可得n＝，A、B、C错误，D正确。

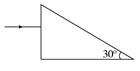
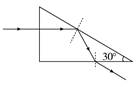
答案　D

7．如图所示，一束光从空气中垂直入射到折射率为的直角三棱镜。求从棱镜第一次射出的光线与原入射方向的偏转角度。

解析　如图所示，光线射到斜边时，i＝60°

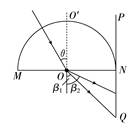
设全反射的临界角为C，因为：sinC＝＝，sini＝，可得sini>sinC，即i＞C，故光射到斜边上时发生全发射。

由几何关系知，光反射到另一直角边时的入射角：

i′＝30°

设光从另一直角边射出时的折射角为r，则由折射率的定义有

＝，得：r＝60°

所以从棱镜第一次射出的光线与原入射方向的偏转角为：α＝90°－60°＝30°。

答案　30°

8．半径为R的固定半圆柱形玻璃砖的横截面如图所示，O点为圆心，OO′为直径MN的垂线，足够大的光屏PQ紧靠在玻璃砖的右侧且与MN垂直。一束复色光沿半径方向与OO′成θ＝30°角射向O点，已知复色光包含折射率从n₁＝到n₂＝的光束，因而光屏上出现了彩色光带。

(1)求彩色光带的宽度；

(2)当复色光入射角逐渐增大时，光屏上的彩色光带将变成一个光点，求θ角至少为多少时会出现这种现象。

解析　(1)由折射定律得n₁＝，n₂＝，代入数据，解得β₁＝45°，β₂＝60°。

故彩色光带的宽度为Rtan45°－Rtan30°＝R。

(2)当所有光线均发生全反射时，光屏上的光带消失，反射光束将在PN上形成一个光点。当折射率为n₁的单色光在玻璃表面上恰好发生全反射时，对应的θ值最小，因为sinC₁＝＝，所以C₁＝45°，故θ的最小值θ_min＝C₁＝45°。

答案　(1)R　(2)45°