专题强化六 动力学和能量观点的综合应用
2.学好本专题,可以极大的培养同学们的审题能力、推理能力和规范表达能力,针对性的专题强化,可以提升同学们解决压轴题的信心. 3.用到的知识有:动力学方法观点(牛顿运动定律、运动学基本规律),能量观点(动能定理、机械能守恒定律、能量守恒定律).
命题点一 多运动组合问题 1.多运动组合问题主要是指直线运动、平抛运动和竖直面内圆周运动的组合问题. 2.解题策略 (1)动力学方法观点:牛顿运动定律、运动学基本规律. (2)能量观点:动能定理、机械能守恒定律、能量守恒定律. 3.解题关键 (1)抓住物理情景中出现的运动状态和运动过程,将物理过程分解成几个简单的子过程. (2)两个相邻过程连接点的速度是联系两过程的纽带,也是解题的关键.很多情况下平抛运动的末速度的方向是解题的重要突破口.
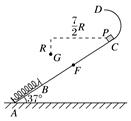
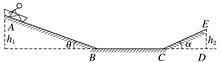
图1 (1)求P第一次运动到B点时速度的大小; (2)求P运动到E点时弹簧的弹性势能; (3)改变物块P的质量,将P推至E点,从静止开始释放.已知P自圆弧轨道的最高点D处水平飞出后,恰好通过G点.G点在C点左下方,与C点水平相距R、竖直相距R,求P运动到D点时速度的大小和改变后P的质量.
答案 (1)2 (2)mgR (3) m 解析 (1)由题意可知:lBC=7R-2R=5R① 设P到达B点时的速度为vB,由动能定理得 mglBCsin θ-μmglBCcos θ=mv② 式中θ=37°,联立①②式并由题给条件得 vB=2③ (2)设BE=x,P到达E点时速度为零,此时弹簧的弹性势能为Ep,由B→E过程,根据动能定理得 mgxsin θ-μmgxcos θ-Ep=0-mv④ E、F之间的距离l1为l1=4R-2R+x⑤ P到达E点后反弹,从E点运动到F点的过程中,由动能定理有 Ep-mgl1sin θ-μmgl1cos θ=0⑥ 联立③④⑤⑥式得 x=R⑦ Ep=mgR⑧ (3)设改变后P的质量为m1,D点与G点的水平距离为x1、竖直距离为y1,由几何关系(如图所示)得θ=37°.
由几何关系得: x1=R-Rsin θ=3R⑨ y1=R+R+Rcos θ=R⑩ 设P在D点的速度为vD,由D点运动到G点的时间为t. 由平抛运动公式得: y1=gt2⑪ x1=vDt⑫ 联立⑨⑩⑪⑫得 vD=⑬ 设P在C点速度的大小为vC,在P由C运动到D的过程中机械能守恒,有 m1v=m1v+m1g(R+Rcos θ)⑭ P由E点运动到C点的过程中,由动能定理得 Ep-m1g(x+5R)sin θ-μm1g(x+5R)cos θ=m1v⑮ 联立⑦⑧⑬⑭⑮得 m1=m.
多过程问题的解题技巧 1.“合”——初步了解全过程,构建大致的运动图景. 2.“分”——将全过程进行分解,分析每个过程的规律. 3.“合”——找到子过程的联系,寻找解题方法.
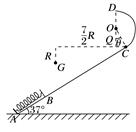
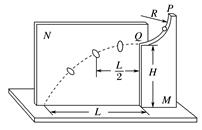
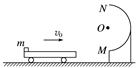
1.同学们参照伽利略时期演示平抛运动的方法制作了如图2所示的实验装置.图中水平放置的底板上竖直地固定有M板和N板.M板上部有一半径为R的圆弧形的粗糙轨道,P为最高点,Q为最低点,Q点处的切线水平,距底板高为H.N板上固定有三个圆环.将质量为m的小球从P处静止释放,小球运动至Q飞出后无阻碍地通过各圆环中心,落到底板上距Q水平距离为L处.不考虑空气阻力,重力加速度为g.求:
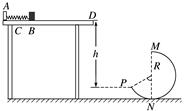
图2 (1)距Q水平距离为的圆环中心到底板的高度; (2)小球运动到Q点时速度的大小以及对轨道压力的大小和方向; (3)摩擦力对小球做的功. 答案 (1)H (2)L mg(1+),方向竖直向下 (3)mg(-R) 解析 (1)由H=gt2和L=vQt可得距Q水平距离为的圆环中心到底板的高度为H. (2)由(1)可得速度的大小vQ=L, 在Q点由牛顿第二定律有FN-mg=m, 对轨道压力的大小FN′=FN=mg(1+),方向竖直向下. (3)由动能定理有mgR+Wf=mv-0,故摩擦力对小球做的功Wf=mg(-R). 2.如图3所示,水平桌面上有一轻弹簧,左端固定在A点,自然状态时其右端位于B点.水平桌面右侧有一竖直放置的轨道MNP,其形状为半径R=1.0 m的圆环剪去了左上角120°的圆弧,MN为其竖直直径,P点到桌面的竖直距离是h=2.4 m.用质量为m=0.2 kg的物块将弹簧缓慢压缩到C点后释放,物块经过B点后做匀变速运动,其位移与时间的关系为x=6t-2t2,物块飞离桌面后恰好由P点沿切线落入圆轨道.(不计空气阻力,g取10 m/s2)
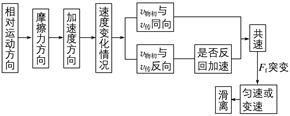
图3 (1)求物块过B点时的瞬时速度大小vB及物块与桌面间的动摩擦因数μ; (2)若轨道MNP光滑,求物块经过轨道最低点N时对轨道的压力FN; (3)若物块刚好能到达轨道最高点M,求物块从B点到M点运动的过程中克服摩擦力所做的功W. 答案 (1)6 m/s 0.4 (2)16.8 N,方向竖直向下 (3)4.4 J 解析 (1)物块过B点后遵从x=6t-2t2, 所以知:vB=6 m/s,a=-4 m/s2. 由牛顿第二定律:-μmg=ma,解得μ=0.4. (2)物块竖直方向的分运动为自由落体运动 P点速度在竖直方向的分量vy==4 m/s P点速度在水平方向的分量vx=vytan 30°=4 m/s 解得离开D点的速度为vD=4 m/s 由机械能守恒定律,有 mv=mv+mg(h+R-Rcos 60°) 解得v=74 m2/s2 根据牛顿第二定律,有FN′-mg=m 解得FN′=16.8 N 根据牛顿第三定律,FN=FN′=16.8 N,方向竖直向下 (3)物块刚好能到达M点,有mg=m 解得vM== m/s 物块到达P点的速度vP==8 m/s 从P到M点应用动能定理,有 -mgR(1+cos 60°)-WPNM=mv-mv 解得WPNM=2.4 J. 从B到D点应用动能定理有-WBD=mv-mv 解得WBD=2 J. 物块从B点到M点的运动过程中克服摩擦力所做的功为2.4 J+2 J=4.4 J. 命题点二 传送带模型问题 1.模型分类:水平传送带问题和倾斜传送带问题. 2.处理方法:求解的关键在于认真分析物体与传送带的相对运动情况,从而确定其是否受到滑动摩擦力作用.如果受到滑动摩擦力作用应进一步确定其大小和方向,然后根据物体的受力情况确定物体的运动情况.当物体速度与传送带速度相等时,物体所受的摩擦力有可能发生突变.
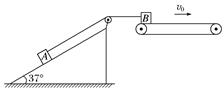
图4 (1)B向右运动的总时间; (2)B回到传送带左端的速度大小; (3)上述过程中,B与传送带间因摩擦产生的总热量.
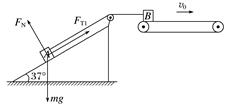
答案 (1)2 s (2)2 m/s (3)(16+4) J 解析 (1)B向右减速运动的过程中,刚开始时,B的速度大于传送带的速度,以B为研究对象,水平方向B受到向左的摩擦力与绳对B的拉力,设绳子的拉力为FT1,以向左为正方向,得FT1+μmg=ma1① 以A为研究对象,则A的加速度的大小始终与B相等,A向上运动的过程中受力如图,则
mgsin 37°-FT1=ma1② 联立①②可得a1==4 m/s2③ B的速度与传送带的速度相等时所用的时间 t1==1 s. 当B的速度与传送带的速度相等之后,B仍然做减速运动,而此时B的速度小于传送带的速度,所以受到的摩擦力变成了向右,所以其加速度发生了变化,此后B向右减速运动的过程中,设绳子的拉力为FT2,以B为研究对象,水平方向B受到向右的摩擦力与绳对B的拉力,则FT2-μmg=ma2④ 以A为研究对象,则A的加速度的大小始终与B是相等的,A向上运动的过程中 mgsin 37°-FT2=ma2⑤ 联立④⑤可得a2==2 m/s2. 当B向右速度减为0,经过时间 t2==1 s. B向右运动的总时间t=t1+t2=1 s+1 s=2 s. (2)B向左运动的过程中,受到的摩擦力的方向仍然向右,仍然受到绳子的拉力,同时,A受到的力也不变,所以它们受到的合力不变,所以B的加速度a3=a2=2 m/s2. t1时间内B的位移x1=t1=-4 m, 负号表示方向向右. t2时间内B的位移x2=×t2=-1 m, 负号表示方向向右. B的总位移x=x1+x2=-5 m. B回到传送带左端的位移x3=-x=5 m. 速度v==2 m/s. (3)t1时间内传送带的位移x1′=-v0t1=-2 m, 该时间内传送带相对于B的位移Δx1=x1′-x1=2 m. t2时间内传送带的位移x2′=-v0t2=-2 m, 该时间内传送带相对于B的位移Δx2=x2-x2′=1 m. B回到传送带左端的时间为t3,则t3== s. t3时间内传送带的位移x3′=-v0t3=-2 m, 该时间内传送带相对于B的位移 Δx3=x3-x3′=(5+2) m. B与传送带之间的摩擦力Ff=μmg=2 N. 上述过程中,B与传送带间因摩擦产生的总热量 Q=Ff(Δx1+Δx2+Δx3)=(16+4) J.
1.分析流程
2.功能关系 (1)功能关系分析:WF=ΔEk+ΔEp+Q. (2)对WF和Q的理解: ①传送带的功:WF=Fx传; ②产生的内能Q=Ffx相对.
3.如图5所示,传送带与地面的夹角θ=37°,A、B两端间距L=16 m,传送带以速度v=10 m/s沿顺时针方向运动,物体质量m=1 kg无初速度地放置于A端,它与传送带间的动摩擦因数μ=0.5,sin 37°=0.6,g=10 m/s2,试求:
图5 (1)物体由A端运动到B端的时间; (2)系统因摩擦产生的热量. 答案 (1)2 s (2)24 J 解析 (1)物体刚放上传送带时受到沿斜面向下的滑动摩擦力,由牛顿第二定律得mgsin θ+μmgcos θ=ma1,设物体经时间t加速到与传送带同速,则v=a1t1,x1=a1t,可解得a1=10 m/s2,t1=1 s,x1=5 m 因mgsin θ>μmgcos θ,故当物体与传送带同速后,物体将继续加速 mgsin θ-μmgcos θ=ma2 L-x1=vt2+a2t 解得t2=1 s 故物体由A端运动到B端的时间 t=t1+t2=2 s (2)物体与传送带间的相对位移 x相对=(vt1-x1)+(L-x1-vt2)=6 m 故Q=μmgcos θ·x相对=24 J. 4.一质量为M=2.0 kg的小物块随足够长的水平传送带一起运动,被一水平向左飞来的子弹击中并从物块中穿过,子弹和小物块的作用时间极短,如图6甲所示.地面观察者记录了小物块被击中后的速度随时间变化的关系如图乙所示(图中取向右运动的方向为正方向).已知传送带的速度保持不变,g取10 m/s2.
图6 (1)指出传送带速度v的大小及方向,说明理由. (2)计算物块与传送带间的动摩擦因数μ. (3)传送带对外做了多少功?子弹射穿物块后系统有多少能量转化为内能? 答案 (1)2.0 m/s 方向向右 (2)0.2 (3)24 J 36 J 解析 (1)从v-t图象中可以看出,物块被击穿后,先向左做减速运动,速度为零后,又向右做加速运动,当速度等于2.0 m/s,则随传送带一起做匀速运动,所以,传送带的速度大小为v=2.0 m/s,方向向右. (2)由v-t图象可得,物块在滑动摩擦力的作用下做匀变速运动的加速度 a== m/s2=2.0 m/s2, 由牛顿第二定律得滑动摩擦力Ff=μMg,则物块与传送带间的动摩擦因数μ====0.2. (3)由v-t图象可知,传送带与物块间存在摩擦力的时间只有3 s,传送带在这段时间内移动的位移为x,则x=vt=2.0×3 m=6.0 m, 所以,传送带所做的功W=Ffx=0.2×2.0×10×6.0 J=24 J. 设物块被击中后的初速度为v1,向左运动的时间为t1,向右运动直至和传送带达到共同速度的时间为t2,则有 物块向左运动时产生的内能 Q1=μMg(vt1+t1)=32 J, 物块向右运动时产生的内能 Q2=μMg(vt2-t2)=4 J. 所以整个过程产生的内能Q=Q1+Q2=36 J. 命题点三 滑块—木板模型问题 1.滑块—木板模型根据情况可以分成水平面上的滑块—木板模型和斜面上的滑块—木板模型. 2.滑块从木板的一端运动到另一端的过程中,若滑块和木板沿同一方向运动,则滑块的位移和木板的位移之差等于木板的长度;若滑块和木板沿相反方向运动,则滑块的位移和木板的位移之和等于木板的长度. 3.此类问题涉及两个物体、多个运动过程,并且物体间还存在相对运动,所以应准确求出各物体在各个运动过程中的加速度(注意两过程的连接处加速度可能突变),找出物体之间的位移(路程)关系或速度关系是解题的突破口,求解中应注意联系两个过程的纽带,每一个过程的末速度是下一个过程的初速度.
甲
图7 (1)在木板右端施加水平向右的拉力F,为使木板和物块发生相对运动,拉力F至少应为多大? (2)在0~4 s内,若拉力F的变化如图乙所示,2 s后木板进入μ2=0.25的粗糙水平面,在图丙中画出0~4 s内木板和物块的v-t图象,并求出0~4 s内物块相对木板的位移大小和整个系统因摩擦而产生的内能. 答案 (1)8 N (2)见解析 解析 (1)把物块和木板看成整体,由牛顿第二定律得F=(m1+m2)a 物块与木板将要相对滑动时, μ1m1g=m1a 联立解得F=μ1(m1+m2)g=8 N. (2)物块在0~2 s内做匀加速直线运动,木板在0~1 s内做匀加速直线运动,在1~2 s内做匀速运动,2 s后物块和木板均做匀减速直线运动,故二者在整个运动过程中的v-t图象如图所示.
0~2 s内物块相对木板向左运动,2~4 s内物块相对木板向右运动. 0~2 s内物块相对木板的位移大小Δx1=2 m, 系统摩擦产生的内能Q1=μ1m1gΔx1=4 J. 2~4 s内物块相对木板的位移大小Δx2=1 m, 物块与木板因摩擦产生的内能Q2=μ1m1gΔx2=2 J; 木板对地位移x2=3 m, 木板与地面因摩擦产生的内能 Q3=μ2(m1+m2)gx2=30 J. 0~4 s内系统因摩擦产生的总内能为 Q=Q1+Q2+Q3=36 J.
滑块—木板模型问题的分析和技巧 1.解题关键 正确地对各物体进行受力分析(关键是确定物体间的摩擦力方向),并根据牛顿第二定律确定各物体的加速度,结合加速度和速度的方向关系确定物体的运动情况. 2.规律选择 既可由动能定理和牛顿运动定律分析单个物体的运动,又可由能量守恒定律分析动能的变化、能量的转化,在能量转化过程往往用到ΔE内=-ΔE机=Ffx相对,并要注意数学知识(如图象法、归纳法等)在此类问题中的应用.
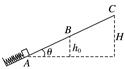
5.如图8所示,一劲度系数很大的轻弹簧一端固定在倾角为θ=30°的斜面底端,将弹簧压缩至A点锁定,然后将一质量为m的小物块紧靠弹簧放置,物块与斜面间动摩擦因数μ=,解除弹簧锁定,物块恰能上滑至B点,A、B两点的高度差为h0,已知重力加速度为g.
图8 (1)求弹簧锁定时具有的弹性势能Ep. (2)求物块从A到B的时间t1与从B返回到A的时间t2之比. (3)若每当物块离开弹簧后,就将弹簧压缩到A点并锁定,物块返回A点时立刻解除锁定.设斜面最高点C的高度H=2h0,试通过计算判断物块最终能否从C点抛出? 答案 (1)mgh0 (2) (3)见解析 解析 (1)物块受到的滑动摩擦力Ff=μmgcos θ, A到B过程由功能关系有-Ff=mgh0-Ep, 解得Ep=mgh0. (2)设上升、下降过程物块加速度大小分别为a1和a2,则 mgsin θ+μmgcos θ=ma1, mgsin θ-μmgcos θ=ma2, 由运动学公式得a1t=a2t,解得=. (3)足够长时间后,上升的最大高度设为hm,则由能量关系,来回克服阻力做功等于补充的弹性势能 2Ff·=Ep, 解得hm=h0<2h0,所以物块不可能到达C点.
题组1 多运动组合问题 1.如图1所示,有两条滑道平行建造,左侧相同而右侧有差异,一个滑道的右侧水平,另一个的右侧是斜坡.某滑雪者保持一定姿势坐在雪撬上不动,从h1高处的A点由静止开始沿倾角为θ的雪道下滑,最后停在与A点水平距离为s的水平雪道上.接着改用另一个滑道,还从与A点等高的位置由静止开始下滑,结果能冲上另一个倾角为α的雪道上h2高处的E点停下.若动摩擦因数处处相同,且不考虑雪橇在路径转折处的能量损失,则( )
图1 A.动摩擦因数为tan θ B.动摩擦因数为 C.倾角α一定大于θ D.倾角α可以大于θ 答案 B 解析 第一次停在水平雪道上,由动能定理得 mgh1-μmgcos θ·-μmgs′=0 mgh1-μmg(+s′)=0 mgh1-μmgs=0 μ= A错误,B正确. 在AB段由静止下滑,说明μmgcos θ<mgsin θ,第二次滑上CE在E点停下,说明μmgcos α>mgsin α;若α>θ,则雪橇不能停在E点,所以C、D错误. 2.如图2所示,将质量为m=1 kg的小物块放在长为L=1.5 m的小车左端,车的上表面粗糙,物块与车上表面间动摩擦因数μ=0.5,直径d=1.8 m的光滑半圆形轨道固定在水平面上且直径MON竖直,车的上表面和轨道最低点高度相同,距地面高度h=0.65 m,开始车和物块一起以10 m/s的初速度在光滑水平面上向右运动,车碰到轨道后立即停止运动,取g=10 m/s2,求:
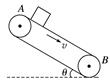
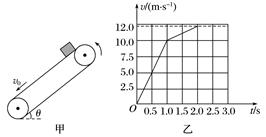
图2 (1)小物块刚进入半圆形轨道时对轨道的压力; (2)小物块落地点至车左端的水平距离. 答案 (1)104.4 N,方向竖直向下 (2)3.4 m 解析 (1)车停止运动后取小物块为研究对象,设其到达车右端时的速度为v1,由动能定理得 -μmgL=mv-mv 解得v1= m/s 刚进入半圆形轨道时,设物块受到的支持力为FN,由牛顿第二定律得 FN-mg=m 又d=2R 解得FN≈104.4 N 由牛顿第三定律FN=FN′ 得FN′=104.4 N,方向竖直向下. (2)若小物块能到达半圆形轨道最高点, 则由机械能守恒得 mv=2mgR+mv 解得v2=7 m/s 设恰能过最高点的速度为v3,则mg=m 解得v3==3 m/s 因v2>v3,故小物块从半圆形轨道最高点做平抛运动, h+2R=gt2,x=v2t 联立解得x=4.9 m 故小物块距车左端为x-L=3.4 m. 题组2 传送带模型问题 3.(多选)如图3甲所示,倾角为θ的足够长的传送带以恒定的速率v0沿逆时针方向运行,t=0时,将质量m=1 kg的物体(可视为质点)轻放在传送带上,物体相对地面的v-t图象如图乙所示.设沿传送带向下为正方向,取重力加速度g=10 m/s2,则( )
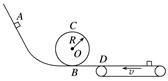
图3 A.传送带的速率v0=10 m/s B.传送带的倾角θ=30° C.物体与传送带之间的动摩擦因数μ=0.5 D.0~2.0 s摩擦力对物体做功Wf=-24 J 答案 ACD 解析 当物体的速度超过传送带的速度后,物体受到的摩擦力的方向发生改变,加速度也发生改变,根据v-t图象可得,传送带的速率为v0=10 m/s,选项A正确;1.0 s之前的加速度a1=10 m/s2,1.0 s之后的加速度a2=2 m/s2,结合牛顿第二定律,gsin θ+μgcos θ=a1,gsin θ-μgcos θ=a2,解得sin θ=0.6,θ=37°,μ=0.5,选项B错误,选项C正确;摩擦力大小Ff=μmgcos θ=4 N,在0~1.0 s内,摩擦力对物体做正功,在1.0~2.0 s内,摩擦力对物体做负功,0~1.0 s内物体的位移为5 m,1.0~2.0 s内物体的位移是11 m,摩擦力做的功为-4×(11-5) J=-24 J,选项D正确. 4.(多选)如图4所示,光滑轨道ABCD是大型游乐设施过山车轨道的简化模型,最低点B处的入、出口靠近但相互错开,C是半径为R的圆形轨道的最高点,BD部分水平,末端D点与右端足够长的水平传送带无缝连接,传送带以恒定速度v逆时针转动,现将一质量为m的小滑块从轨道AB上某一固定位置A由静止释放,滑块能通过C点后再经D点滑上传送带,则( )
图4 A.固定位置A到B点的竖直高度可能为2R B.滑块在传送带上向右运动的最大距离与传送带速度v有关 C.滑块可能重新回到出发点A处 D.传送带速度v越大,滑块与传送带摩擦产生的热量越多 答案 CD 解析 设AB的高度为h,假设滑块从A点下滑刚好通过最高点C,则此时应该是从A下滑的高度的最小值,刚好通过最高点时,由重力提供向心力,则mg=,解得vC=,从A到C根据动能定理:mg(h-2R)=mv-0,整理得到:h=2.5R,故选项A错误;从A到滑块在传送带上向右运动距离最大,根据动能定理得:mgh-μmgx=0,可以得到x=,可以看出滑块在传送带上向右运动的最大距离与传送带速度v无关,与高度h有关,故选项B错误;滑块在传送带上先做减速运动,可能反向做加速运动,如果再次到达D点时速度大小不变,则根据能量守恒,可以再次回到A点,故选项C正确;滑块与传送带之间产生的热量Q=μmgΔx相对,当传送带的速度越大,则在相同时间内二者相对位移越大,则产生的热量越大,故选项D正确. 5.如图5所示,一质量为m=1 kg的可视为质点的滑块,放在光滑的水平平台上,平台的左端与水平传送带相接,传送带以v=2 m/s的速度沿顺时针方向匀速转动(传送带不打滑).现将滑块缓慢向右压缩轻弹簧,轻弹簧的原长小于平台的长度,滑块静止时弹簧的弹性势能为Ep=4.5 J,若突然释放滑块,滑块向左滑上传送带.已知滑块与传送带间的动摩擦因数为μ=0.2,传送带足够长,取g=10 m/s2.求:
图5 (1)滑块第一次滑上传送带到离开传送带所经历的时间; (2)滑块第一次滑上传送带到离开传送带由于摩擦产生的热量. 答案 (1)3.125 s (2)12.5 J 解析 (1)释放滑块的过程中机械能守恒,设滑块滑上传送带的速度为v1,则Ep=mv,得 v1=3 m/s 滑块在传送带上运动的加速度 a=μg=2 m/s2 滑块向左运动的时间t1==1.5 s 向右匀加速运动的时间t2==1 s 向左的最大位移为x1==2.25 m 向右加速运动的位移为x2==1 m 匀速向右运动的时间为t3==0.625 s 所以t=t1+t2+t3=3.125 s. (2)滑块向左运动x1的位移时,传送带向右的位移为x1′=vt1=3 m 则Δx1=x1′+x1=5.25 m 滑块向右运动x2时,传送带向右的位移为 x2′=vt2=2 m 则Δx2=x2′-x2=1 m Δx=Δx1+Δx2=6.25 m 则产生的热量为Q=μmg·Δx=12.5 J. 题组3 滑块—木板模型问题 6.如图6所示,一质量m=2 kg的长木板静止在水平地面上,某时刻一质量M=1 kg的小铁块以水平向左v0=9 m/s的速度从木板的右端滑上木板.已知木板与地面间的动摩擦因数μ1=0.1,铁块与木板间的动摩擦因数μ2=0.4,取重力加速度g=10 m/s2,木板足够长,求:
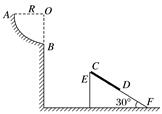
图6 (1)铁块相对木板滑动时木板的加速度的大小; (2)铁块与木板摩擦所产生的热量Q和木板在水平地面上滑行的总路程x. 答案 (1)0.5 m/s2 (2)36 J 1.5 m 解析 (1)设铁块在木板上滑动时,木板的加速度为a2,由牛顿第二定律可得μ2Mg-μ1(M+m)g=ma2, 解得a2= m/s2=0.5 m/s2. (2)设铁块在木板上滑动时,铁块的加速度为a1,由牛顿第二定律得μ2Mg=Ma1,解得a1=μ2g=4 m/s2. 设铁块与木板相对静止达共同速度时的速度为v,所需的时间为t,则有v=v0-a1t,v=a2t, 解得:v=1 m/s,t=2 s. 铁块相对地面的位移 x1=v0t-a1t2=9×2 m-×4×4 m=10 m. 木板运动的位移x2=a2t2=×0.5×4 m=1 m, 铁块与木板的相对位移Δx=x1-x2=10 m-1 m=9 m, 则此过程中铁块与木板摩擦所产生的热量 Q=FfΔx=μ2MgΔx=0.4×1×10×9 J=36 J. 达共同速度后的加速度为a3,发生的位移为s,则有: a3=μ1g=1 m/s2,s== m=0.5 m. 木板在水平地面上滑行的总路程x=x2+s=1 m+0.5 m=1.5 m. 7.如图7所示,AB段为一半径R=0.2 m的光滑圆弧轨道,EF是一倾角为30°的足够长的光滑固定斜面,斜面上有一质量为0.1 kg的薄木板CD,开始时薄木板被锁定.一质量也为0.1 kg的物块(图中未画出)从A点由静止开始下滑,通过B点后水平抛出,经过一段时间后恰好以平行于薄木板的方向滑上薄木板,在物块滑上薄木板的同时薄木板解除锁定,下滑过程中某时刻物块和薄木板能达到共同速度.已知物块与薄木板间的动摩擦因数μ=.(g=10 m/s2,结果可保留根号)求:
图7 (1)物块到达B点时对圆弧轨道的压力; (2)物块滑上薄木板时的速度大小; (3)达到共同速度前物块下滑的加速度大小及从物块滑上薄木板至达到共同速度所用的时间. 答案 (1)3 N,方向竖直向下 (2) m/s (3)2.5 m/s2 s 解析 (1)物块从A运动到B的过程,由动能定理得: mgR=mv,解得:vB=2 m/s 在B点由牛顿第二定律得:FN-mg=m 解得:FN=3 N 由牛顿第三定律得物块对轨道的压力大小为3 N,方向竖直向下. (2)设物块滑上薄木板时的速度为v,则:cos 30°= 解得:v= m/s. (3)物块和薄木板下滑过程中,由牛顿第二定律得: 对物块:mgsin 30°-μmgcos 30°=ma1 对薄木板:mgsin 30°+μmgcos 30°=ma2 设物块和薄木板达到的共同速度为v′,则: v′=v+a1t=a2t 解得:a1=2.5 m/s2,t= s.
|