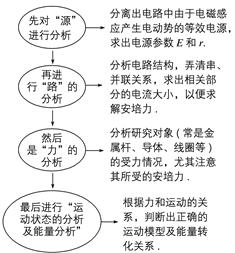
专题强化十一 电磁感应中的动力学和能量问题
2.学好本专题,可以极大培养同学们的分析能力、推理能力和规范表达的能力,针对性的专题强化,可以提升同学们解决电磁感应问题中最难问题的信心. 3.用到的知识有:法拉第电磁感应定律、楞次定律、牛顿运动定律、共点力的平衡条件、动能定理、焦耳定律、能量守恒定律等.
命题点一 电磁感应中的动力学问题 1.题型简述:感应电流在磁场中受到安培力的作用,因此电磁感应问题往往跟力学问题联系在一起.解决这类问题需要综合应用电磁感应规律(法拉第电磁感应定律、楞次定律)及力学中的有关规律(共点力的平衡条件、牛顿运动定律、动能定理等). 2.两种状态及处理方法
3.动态分析的基本思路 解决这类问题的关键是通过运动状态的分析,寻找过程中的临界状态,如速度、加速度最大值或最小值的条件.具体思路如下:
→→→
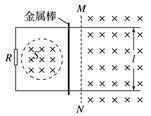
图1 (1)在t=0到t=t0时间间隔内,流过电阻的电荷量的绝对值; (2)在时刻t(t>t0)穿过回路的总磁通量和金属棒所受外加水平恒力的大小. 答案 (1) (2)B0lv0(t-t0)+kSt (B0lv0+kS) 解析 (1)在金属棒未越过MN之前,穿过回路的磁通量的变化量为 ΔΦ=ΔBS=kΔtS① 由法拉第电磁感应定律有 E=② 由欧姆定律得 I=③ 由电流的定义得 I=④ 联立①②③④式得 |Δq|=Δt⑤ 由⑤式得,在t=0到t=t0的时间间隔内即Δt=t0,流过电阻R的电荷量q的绝对值为 |q|=⑥ (2)当t>t0时,金属棒已越过MN.由于金属棒在MN右侧做匀速运动,有 F=F安⑦ 式中,F是外加水平恒力,F安是金属棒受到的安培力.设此时回路中的电流为I, F安=B0lI⑧ 此时金属棒与MN之间的距离为s=v0(t-t0)⑨ 匀强磁场穿过回路的磁通量为 Φ′=B0ls⑩ 回路的总磁通量为 Φt=Φ+Φ′⑪ 其中Φ=B1S=ktS⑫ 由⑨⑩⑪⑫式得,在时刻t(t>t0),穿过回路的总磁通量为Φt=B0lv0(t-t0)+kSt⑬ 在t到t+Δt的时间间隔内,总磁通量的改变量ΔΦt为 ΔΦt=(B0lv0+kS)Δt⑭ 由法拉第电磁感应定律得,回路感应电动势的大小为 Et=⑮ 由欧姆定律得 I=⑯ 联立⑦⑧⑭⑮⑯式得 F=(B0lv0+kS).
1.(多选)如图2所示,两根足够长、电阻不计且相距L=0.2 m的平行金属导轨固定在倾角θ=37°的绝缘斜面上,顶端接有一盏额定电压U=4 V的小灯泡,两导轨间有一磁感应强度大小B=5 T、方向垂直斜面向上的匀强磁场.今将一根长为L、质量为m=0.2 kg、电阻r=1.0 Ω的金属棒垂直于导轨放置在顶端附近无初速度释放,金属棒与导轨接触良好,金属棒与导轨间的动摩擦因数μ=0.25,已知金属棒下滑到速度稳定时,小灯泡恰能正常发光,重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=0.8,则( )
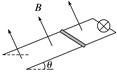
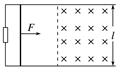
图2 A.金属棒刚开始运动时的加速度大小为3 m/s2 B.金属棒刚开始运动时的加速度大小为4 m/s2 C.金属棒稳定下滑时的速度大小为9.6 m/s D.金属棒稳定下滑时的速度大小为4.8 m/s 答案 BD 解析 金属棒刚开始运动时初速度为零,不受安培力作用,由牛顿第二定律得mgsin θ-μmgcos θ=ma,代入数据得a=4 m/s2,故选项A错误,B正确;设金属棒稳定下滑时速度为v,感应电动势为E,回路中的电流为I,由平衡条件得mgsin θ=BIL+μmgcos θ,由闭合电路欧姆定律得I=,由法拉第电磁感应定律得E=BLv,联立解得v=4.8 m/s,故选项C错误,D正确. 2.如图3所示,水平面(纸面)内间距为l的平行金属导轨间接一电阻,质量为m、长度为l的金属杆置于导轨上.t=0时,金属杆在水平向右、大小为F的恒定拉力作用下由静止开始运动.t0时刻,金属杆进入磁感应强度大小为B、方向垂直于纸面向里的匀强磁场区域,且在磁场中恰好能保持匀速运动.杆与导轨的电阻均忽略不计,两者始终保持垂直且接触良好,两者之间的动摩擦因数为μ.重力加速度大小为g.求:
图3 (1)金属杆在磁场中运动时产生的电动势的大小; (2)电阻的阻值. 答案 (1)Blt0(-μg) (2) 解析 (1)设金属杆进入磁场前的加速度大小为a,由牛顿第二定律得 F-μmg=ma① 设金属杆到达磁场左边界时的速度为v,由运动学公式有v=at0② 当金属杆以速度v在磁场中运动时,由法拉第电磁感应定律知产生的电动势为 E=Blv③ 联立①②③式可得 E=Blt0(-μg)④ (2)设金属杆在磁场区域中匀速运动时,金属杆中的电流为I,根据欧姆定律I=⑤ 式中R为电阻的阻值.金属杆所受的安培力为 F安=BlI⑥ 因金属杆做匀速运动,有 F-μmg-F安=0⑦ 联立④⑤⑥⑦式得R=. 命题点二 电磁感应中的动力学和能量问题 1.题型简述:电磁感应过程的实质是不同形式的能量转化的过程,而能量的转化是通过安培力做功来实现的.安培力做功的过程,是电能转化为其他形式的能的过程;外力克服安培力做功的过程,则是其他形式的能转化为电能的过程. 2.解题的一般步骤 (1)确定研究对象(导体棒或回路); (2)弄清电磁感应过程中,哪些力做功,哪些形式的能量相互转化; (3)根据能量守恒定律或功能关系列式求解. 3.求解电能应分清两类情况 (1)若回路中电流恒定,可以利用电路结构及W=UIt或Q=I2Rt直接进行计算. (2)若电流变化,则 ①利用安培力做功求解:电磁感应中产生的电能等于克服安培力所做的功; ②利用能量守恒求解:若只有电能与机械能的转化,则减少的机械能等于产生的电能.
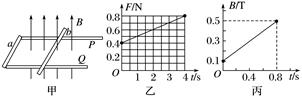
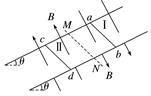
图4 (1)若保持磁感应强度B0的大小不变,从t=0时刻开始,给b棒施加一个水平向右的拉力,使它由静止开始做匀加速直线运动.此拉力F的大小随时间t变化关系如图乙所示.求b棒做匀加速运动的加速度及b棒与轨道间的滑动摩擦力; (2)若从t=0开始,磁感应强度B随时间t按图丙中图象所示的规律变化,求在金属棒b开始运动前,这个装置释放的热量.
答案 (1)5 m/s2 0.2 N (2)0.036 J 解析 (1)F安=B0IL① E=B0Lv② I==③ v=at④ 所以F安=t 当b棒匀加速运动时,根据牛顿第二定律有 F-Ff-F安=ma⑤ 联立可得F-Ff-t=ma⑥ 由图象可得:当t=0时,F=0.4 N,当t=1 s时,F=0.5 N. 代入⑥式,可解得a=5 m/s2,Ff=0.2 N. (2)当磁感应强度均匀增大时,闭合电路中有恒定的感应电流I,以b棒为研究对象,它受到的安培力逐渐增大,静摩擦力也随之增大,当磁感应强度增大到b所受安培力F安′与最大静摩擦力Ff相等时开始滑动 感应电动势E′=L2=0.02 V⑦ I′==1 A⑧ 棒b将要运动时,有F安′=BtI′L=Ff⑨ 所以Bt=1 T,根据Bt=B0+t⑩ 得t=1.8 s,回路中产生的焦耳热为Q=I′2Rt=0.036 J.
能量转化问题的分析程序:先电后力再能量
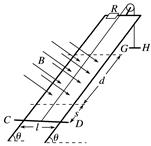
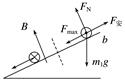
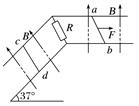
3.(2016·浙江理综·24)小明设计的电磁健身器的简化装置如图5所示,两根平行金属导轨相距l=0.50 m,倾角θ=53°,导轨上端串接一个R=0.05 Ω的电阻.在导轨间长d=0.56 m的区域内,存在方向垂直导轨平面向下的匀强磁场,磁感应强度B=2.0 T.质量m=4.0 kg的金属棒CD水平置于导轨上,用绝缘绳索通过定滑轮与拉杆GH相连.CD棒的初始位置与磁场区域的下边界相距s=0.24 m.一位健身者用恒力F=80 N拉动GH杆,CD棒由静止开始运动,上升过程中CD棒始终保持与导轨垂直.当CD棒到达磁场上边界时健身者松手,触发恢复装置使CD棒回到初始位置(重力加速度g=10 m/s2,sin 53°=0.8,不计其他电阻、摩擦力以及拉杆和绳索的质量).求:
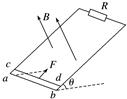
图5 (1)CD棒进入磁场时速度v的大小; (2)CD棒进入磁场时所受的安培力FA的大小; (3)在拉升CD棒的过程中,健身者所做的功W和电阻产生的焦耳热Q. 答案 (1)2.4 m/s (2)48 N (3)64 J 26.88 J 解析 (1)由牛顿第二定律得a==12 m/s2 进入磁场时的速度v==2.4 m/s (2)感应电动势E=Blv 感应电流I= 安培力FA=IBl 代入得FA==48 N (3)健身者做功W=F(s+d)=64 J F-mgsin θ-FA=0 CD棒在磁场区做匀速运动 在磁场中运动时间t= 焦耳热Q=I2Rt=26.88 J. 4.如图6所示,两根足够长的平行金属导轨固定在倾角θ=30°的斜面上,导轨电阻不计,间距L=0.4 m,导轨所在空间被分成区域Ⅰ和Ⅱ,两区域的边界与斜面的交线为MN.Ⅰ中的匀强磁场方向垂直斜面向下,Ⅱ中的匀强磁场方向垂直斜面向上,两磁场的磁感应强度大小均为B=0.5 T.在区域Ⅰ中,将质量m1=0.1 kg、电阻R1=0.1 Ω的金属条ab放在导轨上,ab刚好不下滑.然后,在区域Ⅱ中将质量m2=0.4 kg、电阻R2=0.1 Ω的光滑导体棒cd置于导轨上,由静止开始下滑.cd在滑动过程中始终处于区域Ⅱ的磁场中,ab、cd始终与导轨垂直且两端与导轨保持良好接触,取g=10 m/s2,问:
图6 (1)cd下滑的过程中,ab中的电流方向; (2)ab刚要向上滑动时,cd的速度v为多大; (3)从cd开始下滑到ab刚要向上滑动的过程中,cd滑动的距离x=3.8 m,此过程中ab上产生的热量Q是多少. 答案 (1)由a流向b (2)5 m/s (3)1.3 J
解析 (1)由右手定则可判断出cd中的电流方向为由d到c,则ab中电流方向为由a流向b. (2)开始放置时ab刚好不下滑,ab所受摩擦力为最大静摩擦力,设其为Fmax,有Fmax=m1gsin θ① 设ab刚要上滑时,cd棒的感应电动势为E,由法拉第电磁感应定律有E=BLv② 设电路中的感应电流为I,由闭合电路欧姆定律有 I=③ 设ab所受安培力为F安,有F安=BIL④ 此时ab受到的最大静摩擦力方向沿斜面向下,由平衡条件有F安=m1gsin θ+Fmax⑤ 综合①②③④⑤式,代入数据解得v=5 m/s (3)设cd棒运动过程中在电路中产生的总热量为Q总,由能量守恒定律有m2gxsin θ=Q总+m2v2 又Q=Q总 解得Q=1.3 J
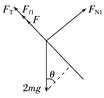
题组1 电磁感应中的动力学问题 1.如图1所示,两固定的绝缘斜面倾角均为θ,上沿相连.两细金属棒ab(仅标出a端)和cd(仅标出c端)长度均为L,质量分别为2m和m;用两根不可伸长的柔软轻导线将它们连成闭合回路abdca,并通过固定在斜面上沿的两光滑绝缘小定滑轮跨放在斜面上,使两金属棒水平.右斜面上存在匀强磁场,磁感应强度大小为B,方向垂直于斜面向上,已知两根导线刚好不在磁场中,回路电阻为R,两金属棒与斜面间的动摩擦因数均为μ,重力加速度大小为g,已知金属棒ab匀速下滑.求:
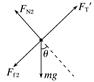
图1 (1)作用在金属棒ab上的安培力的大小; (2)金属棒运动速度的大小. 答案 (1)mg(sin θ-3μcos θ) (2)(sin θ-3μcos θ) 解析 (1)由于ab、cd棒被平行于斜面的导线相连,故ab、cd速度总是相等,cd也做匀速直线运动.设导线的张力的大小为FT,右斜面对ab棒的支持力的大小为FN1,作用在ab棒上的安培力的大小为F,左斜面对cd棒的支持力大小为FN2,对于ab棒,受力分析如图甲所示,由力的平衡条件得
甲 乙 2mgsin θ=μFN1+FT+F① FN1=2mgcos θ② 对于cd棒,受力分析如图乙所示,由力的平衡条件得 mgsin θ+μFN2=FT′=FT③ FN2=mgcos θ④ 联立①②③④式得:F=mg(sin θ-3μcos θ)⑤ (2)设金属棒运动速度大小为v,ab棒上的感应电动势为E=BLv⑥ 回路中电流I=⑦ 安培力F=BIL⑧ 联立⑤⑥⑦⑧得: v=(sin θ-3μcos θ). 2.如图2所示,两平行光滑金属导轨倾斜放置且固定,两导轨间距为L,与水平面间的夹角为θ,导轨下端有垂直于轨道的挡板,上端连接一个阻值R=2r的电阻,整个装置处在磁感应强度为B、方向垂直导轨向上的匀强磁场中,两根相同的金属棒ab、cd放在导轨下端,其中棒ab靠在挡板上,棒cd在沿导轨平面向上的拉力作用下,由静止开始沿导轨向上做加速度为a的匀加速运动.已知每根金属棒质量为m、电阻为r,导轨电阻不计,棒与导轨始终接触良好.求:
图2 (1)经多长时间棒ab对挡板的压力变为零; (2)棒ab对挡板压力为零时,电阻R的电功率; (3)棒ab运动前,拉力F随时间t的变化关系. 答案 (1) (2) (3)F=m(gsin θ+a)+t 解析 (1)棒ab对挡板的压力为零时,受力分析可得 BIabL=mgsin θ 设经时间t0棒ab对挡板的压力为零,棒cd产生的电动势为E,则 E=BLat0 I= R外==r Iab=I 解得t0= (2)棒ab对挡板压力为零时,cd两端电压为 Ucd=E-Ir 解得Ucd= 此时电阻R的电功率为P= 解得P= (3)对cd棒,由牛顿第二定律得 F-BI′L-mgsin θ=ma I′= E′=BLat 解得F=m(gsin θ+a)+t. 题组2 电磁感应中的动力学和能量问题 3.如图3所示,两根相距L=1 m的足够长的光滑金属导轨,一组导轨水平,另一组导轨与水平面成37°角,拐角处连接一阻值R=1 Ω的电阻.质量均为m=2 kg的金属细杆ab、cd与导轨垂直接触形成闭合回路,导轨电阻不计,两杆的电阻均为R=1 Ω.整个装置处于磁感应强度大小B=1 T、方向垂直于导轨平面的匀强磁场中.当ab杆在平行于水平导轨的拉力作用下沿导轨向右匀速运动时,cd杆静止.g=10 m/s2,sin 37°=0.6,cos 37°=0.8,求:
图3 (1)水平拉力的功率; (2)现让cd杆静止,求撤去拉力后ab杆产生的焦耳热. 答案 (1)864 W (2)864 J 解析 (1)cd杆静止,由平衡条件可得mgsin θ=BIL 解得I=12 A 由闭合电路欧姆定律得2I= 得v=36 m/s 水平拉力F=2BIL=24 N 水平拉力的功率P=Fv=864 W (2)撤去外力后ab杆在安培力作用下做减速运动,安培力做负功,先将棒的动能转化为电能,再通过电流做功将电能转化为整个电路产生的焦耳热,即焦耳热等于杆的动能的减小量,有 Q=ΔEk=mv2=1 296 J 而Q=I′2·R·t ab杆产生的焦耳热Q′=I′2·R·t,所以Q′=Q=864 J.
|