实验五 验证机械能守恒定律
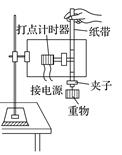
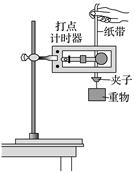
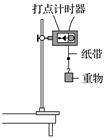
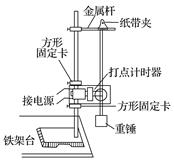
1.实验目的 验证机械能守恒定律. 2.实验原理(如图1所示) 通过实验,求出做自由落体运动物体的重力势能的减少量和相应过程动能的增加量,若二者相等,说明机械能守恒,从而验证机械能守恒定律.
图1 3.实验器材 打点计时器、电源、纸带、复写纸、重物、刻度尺、铁架台(带铁夹)、导线两根. 4.实验步骤 (1)安装器材:将打点计时器固定在铁架台上,用导线将打点计时器与低压电源相连. (2)打纸带 用手竖直提起纸带,使重物停靠在打点计时器下方附近,先接通电源,再松开纸带,让重物自由下落,打点计时器就在纸带上打出一系列的点,取下纸带,换上新的纸带重打几条(3~5条)纸带. (3)选纸带:分两种情况说明 ①若选第1点O到下落到某一点的过程,即用mgh=mv2来验证,应选点迹清晰,且1、2两点间距离小于或接近2 mm的纸带. ②用mv-mv=mgΔh验证时,由于重力势能的相对性,处理纸带时选择适当的点为基准点,这样纸带上打出的第1、2两点间的距离是否小于或接近2 mm就无关紧要了. 5.实验结论 在误差允许的范围内,自由落体运动过程机械能守恒.
1.误差分析 (1)测量误差:减小测量误差的方法,一是测下落距离时都从0点量起,一次将各打点对应下落高度测量完,二是多测几次取平均值. (2)系统误差:由于重物和纸带下落过程中要克服阻力做功,故动能的增加量ΔEk=mv必定稍小于重力势能的减少量ΔEp=mghn,改进办法是调整安装的器材,尽可能地减小阻力. 2.注意事项 (1)打点计时器要竖直:安装打点计时器时要竖直架稳,使其两限位孔在同一竖直平面内,以减少摩擦阻力. (2)重物应选用质量大、体积小、密度大的材料. (3)应先接通电源,让打点计时器正常工作,后松开纸带让重物下落. (4)测长度,算速度:某时刻的瞬时速度的计算应用vn=,不能用vn=或vn=gt来计算. 3.验证方案 方案一:利用起始点和第n点计算 代入mghn和mv,如果在实验误差允许的范围内,mghn和mv相等,则验证了机械能守恒定律. 方案二:任取两点计算 (1)任取两点A、B,测出hAB,算出mghAB. (2)算出mv-mv的值. (3)在实验误差允许的范围内,若mghAB=mv-mv,则验证了机械能守恒定律. 方案三:图象法 从纸带上选取多个点,测量从第一点到其余各点的下落高度h,并计算各点速度的平方v2,然后以v2为纵轴,以h为横轴,根据实验数据作出v2-h图象.若在误差允许的范围内图象是一条过原点且斜率为g的直线,则验证了机械能守恒定律.
命题点一 教材原型实验
图2 (1)为验证机械能是否守恒,需要比较重物下落过程中任意两点间的________. A.动能变化量与势能变化量 B.速度变化量和势能变化量 C.速度变化量和高度变化量 (2)除带夹子的重物、纸带、铁架台(含铁夹)、电磁打点计时器、导线及开关外,在下列器材中,还必须使用的两种器材是________. A.交流电源 B.刻度尺 C.天平(含砝码) (3)实验中,先接通电源,再释放重物,得到图3所示的一条纸带.在纸带上选取三个连续打出的点A、B、C,测得它们到起始点O的距离分别为hA、hB、hC. 已知当地重力加速度为g,打点计时器打点的周期为T.设重物的质量为m.从打O点到打B点的过程中,重物的重力势能变化量ΔEp=__________,动能变化量ΔEk=__________.
图3 (4)大多数学生的实验结果显示,重力势能的减少量大于动能的增加量,原因是________. A.利用公式v=gt计算重物速度 B.利用公式v=计算重物速度 C.存在空气阻力和摩擦阻力的影响 D.没有采用多次实验取平均值的方法 (5)某同学想用下述方法研究机械能是否守恒:在纸带上选取多个计数点,测量它们到起始点O的距离h,计算对应计数点的重物速度v,描绘v2h图象,并做如下判断:若图象是一条过原点的直线,则重物下落过程中机械能守恒,请你分析论证该同学的判断是否正确. 答案 (1)A (2)AB (3)-mghB m()2 (4)C (5)不正确,理由见解析 解析 (1)重物下落过程中重力势能减少,动能增加,故该实验需要比较重物下落过程中任意两点间的动能变化量与势能变化量在误差范围内是否相等,A项正确. (2)电磁打点计时器使用的是交流电源,故要选A.需要测纸带上两点间的距离,还需要刻度尺,选B.根据mgh=mv2-0可将等式两边的质量抵消,不需要天平,不选C. (3)重物的重力势能变化量为ΔEp=-mghB,动能的变化量ΔEk=mv=m()2. (4)重物重力势能的减少量大于动能的增加量,是因为重物下落过程中存在空气阻力和摩擦阻力的影响,C正确. (5)该同学的判断依据不正确,在重物下落h的过程中,若阻力f恒定,根据mgh-fh=mv2-0,则v2=2(g-)h可知,v2h图象就是过原点的一条直线.要想通过v2h图象的方法验证机械能是否守恒,还必须看图象的斜率是否接近2g.
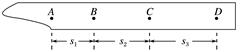
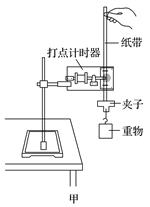
1.某同学用图4(a)所示的实验装置验证机械能守恒定律,其中打点计时器的电源为交流电源,可以使用的频率有20 Hz、30 Hz和40 Hz,打出纸带的一部分如图(b)所示.
(a)
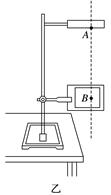
(b) 图4 该同学在实验中没有记录交流电的频率f,需要用实验数据和其他题给条件进行推算. (1)若从打出的纸带可判定重物匀加速下落,利用f和图(b)中给出的物理量可以写出:在打点计时器打出B点时,重物下落的速度大小为________,打出C点时重物下落的速度大小为________,重物下落的加速度大小为________. (2)已测得s1=8.89 cm,s2=9.50 cm,s3=10.10 cm;当地重力加速度大小为9.80 m/s2,实验中重物受到的平均阻力大小约为其重力的1%.由此推算出f为________Hz. 答案 (1)(s1+s2) (s2+s3) (s3-s1) (2)40 解析 (1)由于重物匀加速下落,B点的速度vB等于AC段的平均速度,即vB= 由于T=,故vB=(s1+s2) 同理可得vC=(s2+s3) 匀加速直线运动的加速度a= 故a===(s3-s1)① (2)重物下落的过程中,由牛顿第二定律可得 mg-F阻=ma② 由已知条件F阻=0.01mg③ 由②③得a=0.99g 由①得f= ,代入数据得f≈40 Hz. 2.如图5是用“落体法”验证机械能守恒定律的实验装置.(g取9.80 m/s2)
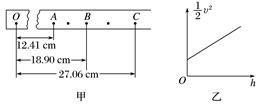
图5 (1)选出一条清晰的纸带如图6甲所示,其中O点为打点计时器打下的第一个点,A、B、C为三个计数点,打点计时器通以频率为50 Hz的交变电流.用分度值为1 mm的刻度尺测得OA=12.41 cm,OB=18.90 cm,OC=27.06 cm,在计数点A和B、B和C之间还各有一个点,重锤的质量为1.00 kg.甲同学根据以上数据算出:当打点计时器打到B点时重锤的重力势能比开始下落时减少了______J;此时重锤的速度vB=______m/s,此时重锤的动能比开始下落时增加了______J.(结果均保留三位有效数字)
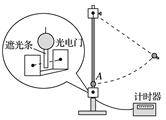
图6 (2)某同学利用他自己实验时打出的纸带,测量出了各计数点到打点计时器打下的第一个点的距离h,算出了各计数点对应的速度v,然后以h为横轴、以v2为纵轴作出了如图乙所示的图线,图线的斜率近似等于______. A.19.6 B.9.8 C.4.90 图线未过原点O的原因是______________________. 答案 (1)1.85 1.83 1.67 (2)B 先释放了纸带,再合上打点计时器的开关 解析 (1)当打点计时器打到B点时,重锤的重力势能减少量ΔEp=mg·OB=1.00×9.80×18.90×10-2 J≈1.85 J;打B点时重锤的速度vB== m/s≈1.83 m/s,此时重锤的动能增加量ΔEk=mv=×1.00×1.832 J≈1.67 J. (2)由机械守恒定律有mv2=mgh,可得v2=gh,由此可知图线的斜率近似等于重力加速度g,故B正确.由图线可知,h=0时,重锤的速度不等于零,原因是该同学做实验时先释放了纸带,然后才合上打点计时器的开关. 3.某同学用如图7甲所示的实验装置验证机械能守恒定律,发现实验误差较大.为了减小误差,该同学设计出如图乙所示的实验装置来验证机械能守恒定律.实验前调整光电门位置,使小铁球下落通过光电门时球心能挡住激光束.实验时,小铁球从A点自由下落,经过光电门B时,通过毫秒计时器(图中未画出)记录挡光时间t,用毫米刻度尺测出A、B之间的距离h,用游标卡尺测得小铁球的直径d.重力加速度为g.则小铁球通过光电门时的瞬时速度v=________.如果测量的d、t、h、g满足关系式____________,即可验证机械能守恒定律.
图7 答案 =gh 解析 由于小铁球很小,挡光时间t很短,可以用平均速度代替小铁球通过光电门时的瞬时速度,所以小铁球通过光电门时的瞬时速度v=.由机械能守恒定律,小铁球下落过程中减少的重力势能mgh等于增加的动能mv2,即mgh=mv2,将v=代入化简得=gh.即如果测量的d、t、h、g满足关系式=gh,即可验证机械能守恒定律. 命题点二 实验拓展创新
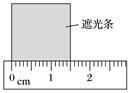
图8 (1)用ΔEp=mgh计算钢球重力势能变化的大小,式中钢球下落高度h应测量释放时的钢球球心到________之间的竖直距离. A.钢球在A点时的顶端 B.钢球在A点时的球心 C.钢球在A点时的底端 (2)用ΔEk=mv2计算钢球动能变化的大小,用刻度尺测量遮光条宽度,示数如图9所示,其读数为________cm.某次测量中,计时器的示数为0.010 0 s,则钢球的速度为v=________m/s.
图9 (3)下表为该同学的实验结果:
他发现表中的ΔEp与ΔEk之间存在差异,认为这是由于空气阻力造成的.你是否同意他的观点?请说明理由. (4)请你提出一条减小上述差异的改进建议. 答案 (1)B (2)1.50 1.50 (3)不同意 理由见解析 (4)见解析 解析 (1)钢球下落高度h,应测量释放时钢球球心到钢球在A点时的球心之间的竖直距离,故选B. (2)遮光条的宽度d=1.50 cm,钢球的速度v==1.50 m/s. (3)不同意,因为空气阻力会造成ΔEk小于ΔEp,但表中ΔEk大于ΔEp. (4)分别测出光电门和球心到悬点的长度L和l,计算ΔEk时,将v折算成钢球的速度v′=v.
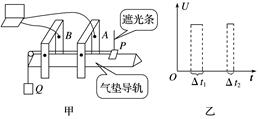
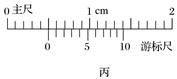
4.某研究性学习小组利用气垫导轨验证机械能守恒定律,实验装置如图10甲所示.在气垫导轨上相隔一定距离的两处安装两个光电传感器A、B,滑块P上固定一遮光条,若光线被遮光条遮挡,光电传感器会输出高电压,两光电传感器采集数据后与计算机相连.滑块在细线的牵引下向左加速运动,遮光条经过光电传感器A、B时,通过计算机可以得到如图乙所示的电压U随时间t变化的图象.
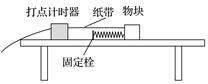
图10 (1)实验前,接通气源,将滑块(不挂钩码)置于气垫导轨上,轻推滑块,当图乙中的Δt1______Δt2(选填“>”“=”或“<”)时,说明气垫导轨已经水平. (2)用游标卡尺测遮光条宽度d,测量结果如图丙所示,则d=______mm. (3)滑块P用细线跨过气垫导轨左端的定滑轮与钩码Q相连,钩码Q的质量为m.将滑块P由图甲所示位置释放,通过计算机得到的图象如图乙所示,若Δt1、Δt2和d已知,要验证滑块和砝码组成的系统机械能是否守恒,还应测出______________________(写出物理量的名称及符号). (4)若上述物理量间满足关系式______________,则表明在上述过程中,滑块和砝码组成的系统机械能守恒. 答案 (1)= (2)5.0 (3)滑块质量M和两光电门间距离L (4)mgL=(m+M)()2-(m+M)()2 解析 (1)实验前,接通气源,将滑块(不挂钩码)置于气垫导轨上,轻推滑块,当图乙中的Δt1=Δt2时,说明滑块已经匀速运动,说明气垫导轨已经水平. (2)用游标卡尺测遮光条宽度d,则d=5.0 mm. (3)滑块经过两个光电门的速度分别为:和,钩码重力势能的减小量为mgL,故要验证的关系是mgL=(m+M)()2-(m+M)()2,故还应测出滑块质量M和两光电门间距离L. (4)若上述物理量间满足关系式mgL=(m+M)()2-(m+M)()2,则表明在上述过程中,滑块和砝码的系统机械能守恒. 5.某物理小组对轻弹簧的弹性势能进行探究,实验装置如图11所示:轻弹簧放置在光滑水平桌面上,弹簧左端固定,右端与一物块接触而不连接,纸带穿过打点计时器并与物块连接.向左推物块使弹簧压缩一段距离,由静止释放物块,通过测量和计算,可求得弹簧被压缩后的弹性势能.
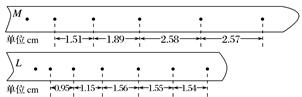
图11 (1)实验中涉及到下列操作步骤: ①把纸带向左拉直 ②松手释放物块 ③接通打点计时器电源 ④向左推物块使弹簧压缩,并测量弹簧压缩量 上述步骤正确的操作顺序是________(填入代表步骤的序号). (2)图12中M和L纸带是分别把弹簧压缩到不同位置后所得到的实际打点结果.打点计时器所用交流电的频率为50 Hz.由M纸带所给的数据,可求出在该纸带对应的实验中物块脱离弹簧时的速度为________m/s.比较两纸带可知,________(填“M”或“L”)纸带对应的实验中弹簧被压缩后的弹性势能大.
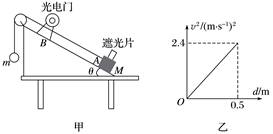
图12 答案 (1)④①③② (2)1.29 M 解析 (1)根据该实验操作过程,正确步骤应为④①③②. (2)物块脱离弹簧时速度最大,v== m/s=1.29 m/s;由动能定理ΔEk=mv2,据纸带中打点的疏密知M纸带获得的最大速度较大,对应的实验中弹簧被压缩后的弹性势能较大. 6.利用气垫导轨验证机械能守恒定律,实验装置如图13甲所示,水平桌面上固定一倾斜的气垫导轨,导轨上A点处有一带长方形遮光片的滑块,其总质量为M,左端由跨过轻质光滑定滑轮的细绳和一质量为m的小球相连;遮光片两条长边与导轨垂直,导轨上B点有一光电门,可以测量遮光片经过光电门时的挡光时间t,用d表示A点到光电门B处的距离,b表示遮光片的宽度,将遮光片通过光电门的平均速度看作滑块通过B点时的瞬时速度,实验时滑块在A处由静止开始运动. (1)某次实验测得倾角θ=30°,重力加速度用g表示,滑块从A处到达B处时m和M组成的系统动能增加量可表示为ΔEk=____________,系统的重力势能减少量可表示为ΔEp=__________,在误差允许的范围内,若ΔEk=ΔEp,则可认为系统的机械能守恒.(用题中字母表示)
图13 (2)在上次实验中,某同学改变A、B间的距离,作出的v2-d图象如图乙所示,并测得M=m,则重力加速度g=________m/s2. 答案 (1) (m-)gd (2)9.6 解析 (1)系统动能增加量可表示为ΔEk=(M+m)v=,系统的重力势能减少量可表示为ΔEp=mgd-Mgdsin 30°=(m-)gd. (2)根据机械能守恒可得(m-)gd=(M+m)v2,即g=,代入数据得g=9.6 m/s2.
|