⊳数学分析能力的培养

⊳析题破题能力的培养

⊳图象应用能力的培养

用极限思想理解两种速度关系

1．两种速度的关系

(1)瞬时速度是运动时间Δt→0时的平均速度．

(2)对于匀速直线运动，瞬时速度与平均速度相等．

2．关于用平均速度法求瞬时速度

(1)方法概述：由平均速度公式v＝可知，当Δx、Δt都非常小，趋向于极限时，这时的平均速度就可认为是某一时刻或某一位置的瞬时速度．

(2)选用思路：当已知物体在微小时间Δt内发生的微小位移Δx时，可由v＝粗略地求出物体在该位置的瞬时速度．

例1　如图1所示，在气垫导轨上安装有两个光电计时装置A、B，A、B间距离为L＝30 cm，为了测量滑块的加速度，在滑块上安装了一个宽度为d＝1 cm的遮光条，现让滑块以某一加速度通过A、B，记录遮光条通过A、B的时间分别为0.010 s、0.005 s，滑块从A到B所用时间为0.200 s，则下列说法正确的是(　　)

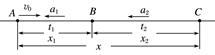
图1

A．滑块通过A的速度为1 cm/s

B．滑块通过B的速度为2 cm/s

C．滑块加速度为5 m/s²

D．滑块在A、B间的平均速度为3 m/s

答案　C

解析　v_A＝＝ m/s＝1 m/s

v_B＝＝2 m/s

a＝＝ m/s²＝5 m/s²

_AB＝＝1.5 m/s.

例2　珠海航展现场空军八一飞行表演队两架“歼－10”飞机表演剪刀对冲，上演精彩空中秀．质量为m的“歼－10”飞机表演后返回某机场，降落在跑道上．减速过程简化为两个匀减速直线运动．飞机以速度v₀着陆后立即打开减速阻力伞，加速度大小为a₁，运动时间为t₁；随后在无阻力伞情况下匀减速直至停下．在平直跑道上减速滑行总路程为x.求第二个减速阶段飞机运动的加速度大小和时间．

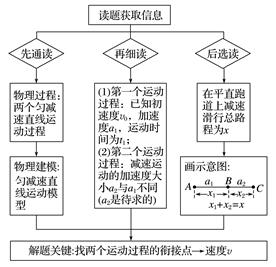
【思维流程】

答案　　

解析　如图所示，设A为飞机着陆点，AB、BC分别为两个匀减速运动过程，在C点停下．

A到B过程，依据运动学规律有：

x₁＝v₀t₁－a₁t₁²

v_B＝v₀－a₁t₁

B到C过程，依据运动学规律有：

x₂＝v_Bt₂－a₂t₂²

0＝v_B－a₂t₂

A到C过程， 有：x＝x₁＋x₂

联立解得：a₂＝；t₂＝.

1．对多过程的运动问题，若用传统的解析法分析，不仅求解困难，而且计算过程复杂，有时甚至难以求出正确答案，此时若依据题中所描述的运动过程画出物体的运动过程图象辅助分析，则可方便求解．

2．对于两个质点分别以不同的加速度运动，比较运动快慢问题时可作速度(速率)—时间图象进行辅助分析，此时根据图象“面积”相等这一特征比较时间长短．

3．所描述的物理量做非线性变化时，可先构建一个物理量与另一物理量的线性变化关系图象，如“反比关系可转化为与倒数成正比”，然后应用“面积”含义或斜率的含义即可求解具体问题．

例3　如图2所示，两光滑斜面的总长度相等，高度也相同，a、b两球由静止从顶端下滑，若球在图上转折点无能量损失，则(　　)

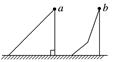
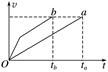
图2

A．a球后着地

B．b球后着地

C．两球同时落地

D．两球着地时速度相同

【思路追踪】

答案　A

解析　本题若采用解析法，难度很大．可利用v－t图象(这里的v是速率，曲线下的面积表示路程s)进行定性比较．在同一个v－t图象中作出a、b的速率图线如图所示，由于开始运动时b的加速度较大，则斜率较大；由机械能守恒可知末速率相同，故曲线末端在同一水平线上，由于两斜面长度相同，则应使图线与t轴围成的“面积”相等．结合图中图线特点可知b用的时间较少，由此可知A正确，B、C、D错误．