⊳思维建模能力的培养

⊳图象应用能力的培养

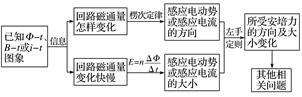
1．“杆＋导轨”模型是电磁感应问题高考命题的“基本道具”，也是高考的热点，考查的知识点多，题目的综合性强，物理情景变化空间大，是我们复习中的难点．“杆＋导轨”模型又分为“单杆”型和“双杆”型(“单杆”型为重点)；导轨放置方式可分为水平、竖直和倾斜；杆的运动状态可分为匀速、匀变速、非匀变速运动等．

2．该模型的解题思路

(1)用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向；

(2)求回路中的电流大小；

(3)分析研究导体受力情况(包含安培力，用左手定则确定其方向)；

(4)列动力学方程或平衡方程求解．

例1　如图1甲所示，两根足够长平行金属导轨MN、PQ相距为L，导轨平面与水平面夹角为α，金属棒ab垂直于MN、PQ放置在导轨上，且始终与导轨接触良好，金属棒的质量为m.导轨处于匀强磁场中，磁场的方向垂直于导轨平面向上，磁感应强度大小为B.金属导轨的上端与开关S、定值电阻R₁和电阻箱R₂相连．不计一切摩擦，不计导轨、金属棒的电阻，重力加速度为g.现在闭合开关S，将金属棒由静止释放．

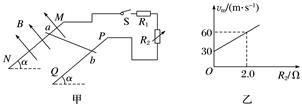
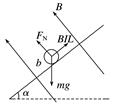
图1

(1)判断金属棒ab中电流的方向；

(2)若电阻箱R₂接入电路的阻值为0，当金属棒下降高度为h时，速度为v，求此过程中定值电阻上产生的焦耳热Q；

(3)当B＝0.40 T，L＝0.50 m，α＝37°时，金属棒能达到的最大速度v_m随电阻箱R₂阻值的变化关系，如图乙所示．取g＝10 m/s²，sin 37°＝0.60，cos 37°＝0.80.求R₁的阻值和金属棒的质量m.

答案　(1)b→a　(2)mgh－mv²　(3)2.0 Ω　0.1 kg

解析　(1)由右手定则可知，金属棒ab中的电流方向为由b到a.

(2)由能量守恒定律知，金属棒减少的重力势能等于增加的动能和电路中产生的焦耳热，即

mgh＝mv²＋Q

则Q＝mgh－mv².

(3)金属棒达到最大速度v_m时，切割磁感线产生的感应电动势：E＝BLv_m

由闭合电路的欧姆定律得：I＝

从b端向a端看，金属棒受力如图所示

金属棒达到最大速度时，满足：

mgsin α－BIL＝0

由以上三式得v_m＝(R₂＋R₁)

由图乙可知：斜率

k＝ m·s^－1·Ω^－1＝15 m·s^－1·Ω^－1

纵轴截距v＝30 m/s

所以R₁＝v，＝k

解得R₁＝2.0 Ω，m＝0.1 kg.

解决此类问题要抓住三点

1．杆的稳定状态一般是匀速运动(达到最大速度或最小速度，此时合力为零)；

2．整个电路产生的电能等于克服安培力所做的功；

3．电磁感应现象遵从能量守恒定律．

分析电磁感应图象问题的思路

例2　如图2所示，矩形闭合导体线框在匀强磁场上方，由不同高度静止释放，用t₁、t₂分别表示线框ab边和cd边刚进入磁场的时刻．线框下落过程形状不变，ab边始终保持与磁场水平边界线OO′平行，线框平面与磁场方向垂直．设OO′下方磁场区域足够大，不计空气的影响，则下列哪一个图象不可能反映线框下落过程中速度v随时间t变化的规律(　　)

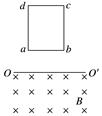
图2

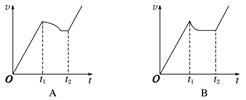
答案　A

解析　线框在0～t₁这段时间内做自由落体运动，v－t图象为过原点的倾斜直线，t₂之后线框完全进入磁场区域中，无感应电流，线框不受安培力，只受重力，线框做匀加速直线运动，v－t图象为倾斜直线．t₁～t₂这段时间线框受到安培力作用，线框的运动类型只有三种，即可能为匀速直线运动、也可能为加速度逐渐减小的加速直线运动，还可能为加速度逐渐减小的减速直线运动，而A选项中，线框做加速度逐渐增大的减速直线运动是不可能的，故不可能的v－t图象为A选项中的图象．